Đề cương ôn tập học kì 2 môn Toán lớp 11 năm 2023-2024 - Trường THPT Phúc Thọ, Hà Nội

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:20

Thêm vào BST

Báo xấu

2
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

TaiLieu.VN giới thiệu đến các bạn “Đề cương ôn tập học kì 2 môn Toán lớp 11 năm 2023-2024 - Trường THPT Phúc Thọ, Hà Nội” để ôn tập nắm vững kiến thức cũng như giúp các em được làm quen trước với các dạng câu hỏi đề thi giúp các em tự tin hơn khi bước vào kì thi chính thức.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề cương ôn tập học kì 2 môn Toán lớp 11 năm 2023-2024 - Trường THPT Phúc Thọ, Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI ĐỀ CƯƠNG ÔN TẬP CUỐI KỲ II TRƯỜNG THPT PHÚC THỌ Năm học: 2023-2024 MÔN: TOÁN 11 Phúc Thọ, ngày 22 tháng 4 năm 2024 I. LÝ THUYẾT 1. Một số yếu tố thống kê và xác suất: - Biến cố hợp, biến cố giao, biến cố độc lập, các quy tắc tính xác suất. 2. Hàm số mũ, hàm số lôgarit: - Phép tính lũy thừa với số mũ thực. - Phép tính loogarit. - Hàm số mũ, hàm số loogarit. - Phương trình, bất phương trình mũ và loogarit. 3. Đạo hàm: - Định nghĩa đạo hàm, ý nghĩa hình học của đạo hàm. - Các quy tắc tính đạo hàm. - Đạo hàm cấp hai. 4. Quan hệ vuông góc trong không gian, phép chiếu vuông góc: - Hai đường thẳng vuông góc. - Đường thẳng vuông góc với mặt phẳng. - Góc giữa đường thẳng và mặt phẳng, góc nhị diện. - Hai mặt phẳng vuông góc. - Khoảng cách. - Hình lăng trụ đứng, hình chóp đều, thể tích của một số hình khối. II. CÂU HỎI ÔN TẬP A. ĐẠI SỐ PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn Câu 1: Cho hai biến cố A và B. Biến cố “ A hoặc B xảy ra” được gọi là A. Biến cố giao của A và B. B. Biến cố đối của A. C. Biến cố hợp của A và B. D. Biến cố đối của B. Câu 2: Cho hai biến cố A và B. Biến cố “ Cả A và B đều xảy ra” được gọi là A. Biến cố giao của A và B. B. Biến cố đối của A. C. Biến cố hợp của A và B. D. Biến cố đối của B. 1 1 Câu 3: ( ) ( ) Cho A, B là hai biến cố xung khắc. Biết P A = ,P B = . Tính P A  B 3 4 ( ) 7 1 1 1 A. B. C. D. 12 12 7 2 Câu 4: Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng, 4 viên bi trắng. Lấy ngẫu nhiên hai bi, tính xác suất biến cố A : “hai viên bi cùng màu”. 4 6 A. P ( A) = . B. P ( A) = . 195 195 4 64 C. P ( A) = . D. P ( A) = . 15 195 Câu 5: Một lớp có 60 sinh viên trong đó 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một sinh
viên. Tính xác suất của các biến cố sinh viên được chọn không học tiếng Anh và tiếng Pháp. 1 1 1 5 A. . B. . C. D. 2 3 6 6 Câu 6: Có hai hộp đựng bi. Hộp I có 9 viên bi được đánh số 1, 2, , 9 . Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số chẵn ở hộp II 3 là . Xác suất để lấy được cả hai viên bi mang số chẵn là: 10 2 1 4 7 A. . B. . C. . D. . 15 15 15 15 Câu 7: Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất làm bàm tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ làm bàn. A. P ( X ) = 0, 42 . B. P ( X ) = 0,94 . C. P ( X ) = 0, 234 . D. P ( X ) = 0,9 . Câu 8: Một cặp vợ chồng mong muốn sinh bằng đựơc sinh con trai. Xác suất sinh được con trai trong một lần sinh là 0, 51 . Tìm xác suất sao cho cặp vợ chồng đó mong muốn sinh được con trai ở lần sinh thứ 2. A. P (C ) = 0, 24 . B. P (C ) = 0, 299 . C. P(C ) = 0, 24239 . D. P (C ) = 0, 2499 . 1 Câu 9: Rút gọn biểu thức P = x . x với x  0 . 3 6 1 2 A. P = x . B. P = x 8 . C. P = x 9 . D. P = x 2 . ( ) 4 4 a 3 .b 2 Câu 10: Cho a , b là các số thực dương. Rút gọn biểu thức P = được kết quả là 3 a12 .b6 A. ab2 . B. a 2 b . C. ab . D. a 2 b 2 . Câu 11: Biểu thức T = 5 a 3 a với a  0 . Viết biểu thức T dưới dạng luỹ thừa với số mũ hữu tỉ là: 3 2 1 4 A. a 5 . B. a 15 . C. a 3 . D. a 15 . 1 1   2 2 1 a b  Câu 12: Cho a  0 , b  0 và biểu thức T = 2 ( a + b ) . ( ab ) −1 2 . 1 +  −  . Khi đó:  4 b a     2 1 1 A. T = . B. T = . C. T = 1 . D. T = . 3 2 3 m m Câu 13: Cho biểu thức 5 8 2 3 2 = 2 n , trong đó là phân số tối giản. Gọi P = m2 + n2 . n Khẳng định nào sau đây đúng? A. P  ( 330; 340 ) . B. P  ( 350; 360 ) . C. P  ( 260; 370 ) . D. P  ( 340; 350 ) .
11 3 m a7 .a 3 Câu 14: Rút gọn biểu thức A = với a  0 ta được kết quả A = a n trong đó a 4 . 7 a −5 m m, n  N * và là phân số tối giản. Khẳng định nào sau đây đúng? n A. m2 − n2 = 312 . B. m2 + n2 = 543 . C. m 2 − n2 = −312 . D. m 2 + n2 = 409. 4 − 2x − 2− x a Câu 15: Cho 4 x + 4 − x = 2 và biểu thức A = = . Tích a.b có giá trị bằng: 1 + 2x + 2− x b A. 6 . B. −10 . C. −8 . D. 8 . Câu 16: Cho các số thực dương a, b thỏa mãn log 2 a = x , log 2 b = y . Tính P = log 2 ( a b ) . 2 3 A. P = x 2 y 3 B. P = x 2 + y 3 C. P = 6 xy D. P = 2 x + 3 y Câu 17: Cho a, b  0 và a, b  1 , biểu thức P = log a b3 .logb a 4 có giá trị bằng bao nhiêu? A. 18 . B. 24 . C. 12 . D. 6 .  1  Câu 18: Cho a  0, a  1 . Tính giá trị của biểu thức P = log 3 a  3  a  A. P = −9 . B. P = −1 . C. P = 1 . D. P = 9 . Câu 19: Cho a là số thực dương và b là số thực khác 0 . Mệnh đề nào sau đây là mệnh đề đúng?  3a3  1 A. log3  2  = 1 + log3 a − 2 log 3 b .  b  3  3a3  B. log3  2  = 1 + 3log 3 a − 2log 3 b .  b   3a3  C. log3  2  = 1 + 3log 3 a − 2log 3 b .  b   3a3  D. log3  2  = 1 + 3log 3 a + 2log 3 b .  b  Câu 20: Đặt a = log 2 3 và b = log 5 3 . Hãy biểu diễn log 6 45 theo a và b . a + 2ab 2a 2 − 2ab A. log 6 45 = . B. log 6 45 = . ab + b ab a + 2ab 2a 2 − 2ab C. log 6 45 = . D. log 6 45 = . ab ab + b Câu 21: Biết log ( xy 3 ) = 1 và log ( x 2 y ) = 1 , tìm log ( xy ) ? 5 1 A. log ( xy ) = . B. log ( xy ) = . 3 2 3 C. log ( xy ) = . D. log ( xy ) = 1 . 5
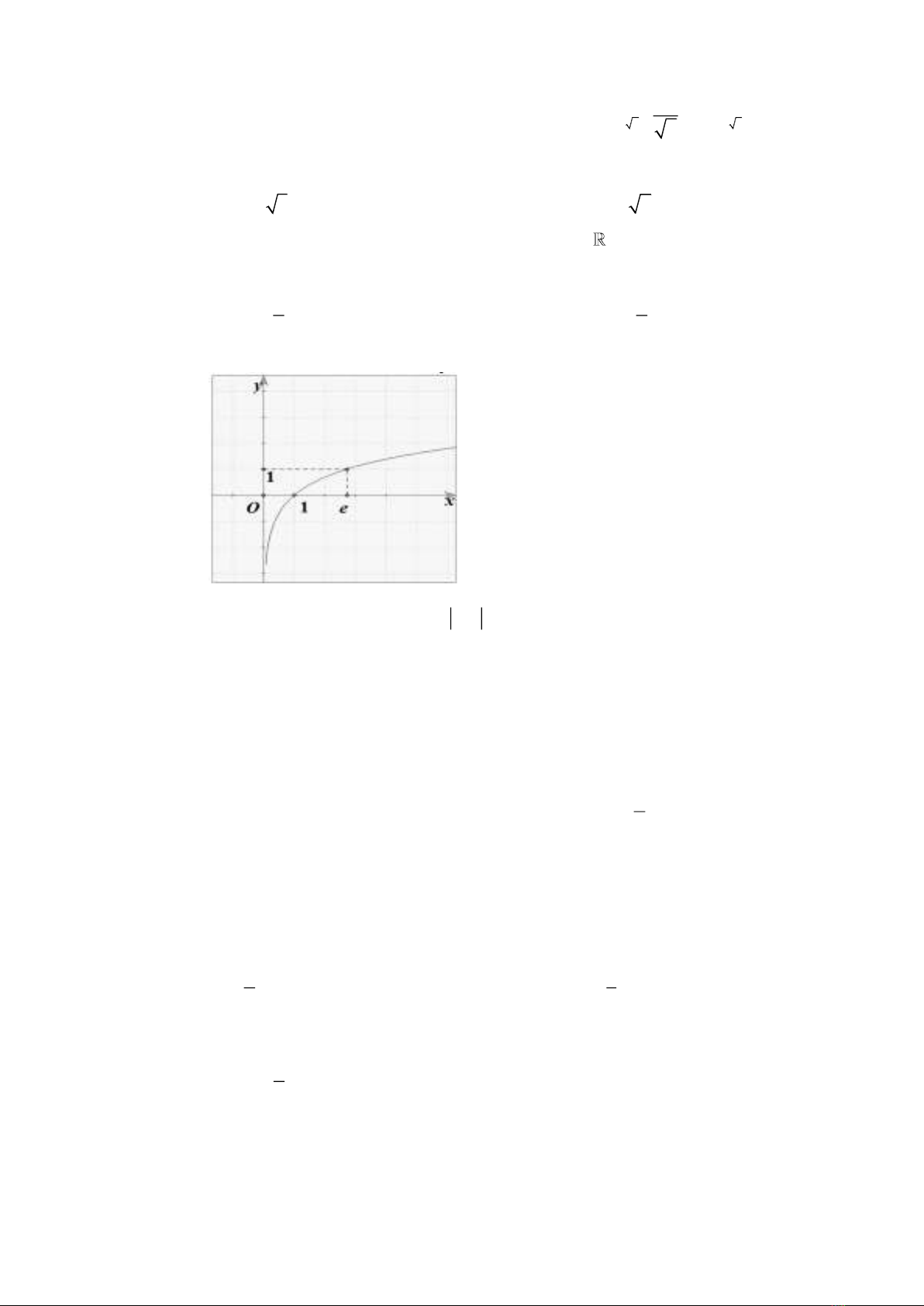
 a  Câu 22: Tính giá trị của biểu thức P = log a2 ( a10b 2 ) + log   + log 3 b b −2 ( với  b a 0  a  1;0  b  1 ). A. P = 2 . B. P = 1 . C. P = 3 . D. P = 2 . Câu 23: Trong các hàm số sau hàm số nào nghịch biến trên ? B. y = log ( x3 ) 2 A. log 3 x x −x e 2 C. y =   D. y =   4 5 Câu 24: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. y = −e x . B. y = ln x . C. y = ln x . D. y = e x . Câu 25: Đồ thị hàm số y = ln( x − e ) đi qua điểm A. ( 1; 0 ) . ( ) B. 2; e 2 . C. ( 2 e ;1) . D. ( e ; 0 ) . Câu 26: Đồ thị hàm số y = 3 x đi qua điểm A. ( 1;1) . B. ( 2; −9 ) .  1 C. ( 2 e ; 2 ) . D.  −2;  .  9 Câu 27: Tìm tập nghiệm của bất phương trình 32 x  3x+ 4 . A. D = ( −; 4 ) . B. D = ( 4; +  ) . C. D = ( −4; +  ) . D. D = ( 0; 4 ) . Câu 28: Tập nghiệm của bất phương trình 32 x−1  27 là: 1  1  A.  ; +  . B. ( 3; + ) . C.  ; +  . D. ( 2; + ) . 2  3  Câu 29: Tập nghiệm S của bất phương trình log 3 ( x + 1)  log 3 ( 2 x − 1) là 1  A. S =  ; 2  . B. S = ( − ; 2 ) . 2  C. S = ( 2; +  ) . D. S = ( −1; 2 ) .
Câu 30: Giải bất phương trình sau log 1 ( 3x − 5 )  log 1 ( x + 1) . 5 5 5 5 A.  x  3 . B. −1  x  3 . C. −1  x  . D. x  3 . 3 3 Câu 31: Dân số nước ta năm 2021 ước tính là 98 564 407 người. Giả sử tỉ lệ tăng dân số hằng năm của nước ta là 0,93% . Biết rằng sau t năm, dân số Việt Nam ( tính từ mốc năm 2021) ước tính theo công thức: S = A.e rt . Hỏi từ năm nào trở đi, dân số nước ta vượt 110 triệu người? A. 2031. B. 2033. C. 2034. D. 2032. Câu 32: Tập nghiệm của bất phương trình 2 x  3x+1 là:   A.  . B.  −;log 2 3  .  3    C. ( −;log 2 3 . D.  log 2 3; +  .  3  Câu 33: Tính số gia của hàm số y = x 3 + x 2 + 1 tại điểm x0 ứng với số gia x = 1. A. y = 3x0 + 5 x0 + 3. 2 B. y = 2 x0 + 3x0 + 5 x0 + 2. 3 2 C. y = 3x0 + 5 x0 + 2. 2 D. y = 3x0 − 5 x0 + 2. 2 x2 Câu 34: Tính số gia của hàm số y = tại điểm x0 = −1 ứng với số gia x. 2 1 1 ( x ) − x. B. y = ( x ) − x  . 2 2 A. y = 2 2   1 1 C. y = ( x ) + x  . D. y = ( x ) + x. 2 2 2   2 y Câu 35: Tính tỷ số của hàm số y 3x 1 theo x và x. x y y y y A. 0. B. 1. C. 2. D. 3. x x x x Câu 36: Cho f là hàm số liên tục tại x 0 . Đạo hàm của f tại x 0 là: A. f x 0 . f x0 h f x0 B. . h f x0 h f x0 C. lim (nếu tồn tại giới hạn) . h 0 h f x0 h f x0 h D. lim (nếu tồn tại giới hạn) . h 0 h Câu 37: Một chất điểm chuyển động có phương trình s ( t ) = t 3 − 3t 2 + 9t + 2 , trong đó t  0, t tính bằng giây và s ( t ) tính bằng mét. Hỏi tại thời điểm nào thì vận tốc của vật đạt giá trị nhỏ nhất? A. t = 1s. B. t = 2s. C. t = 3s. D. t = 6s. Câu 38: Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v ( t ) = 8t + 3t 2 , trong đó t  0, t tính bằng giây và v ( t ) tính bằng mét/giây. Tìm gia tốc của chất điểm tại thời điểm mà vận tốc chuyển động là 11 m / s . A. 6m/s 2 . B. 11m/s 2 . C. 14m/s 2 . D. 20m/s 2 .
Câu 39: Viết phương trình tiếp tuyến của đường cong y x 3 tại điểm 1; 1 . A. y 3 x 4. B. y 1. C. y 3x 2. D. y 3x 2. Câu 40: Cho hàm số y = x 3 − 3 x 2 + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm với đường thẳng y = −2. A. y = −9 x + 7; y = −2. B. y = 5. C. y = 9 x + 7; y = −2. D. y = 9 x + 7; y = 2. Câu 41: Cho hàm số y = x 3 − 3 x 2 + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng y = 9 x + 7. A. y = 9 x + 7; y = 9 x − 25. B. y = 9 x − 25. C. y = 9 x − 7; y = 9 x + 25. D. y = 9 x + 25. Câu 42: Cho hàm số y = x 3 − 3 x 2 + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết 1 tiếp tuyến vuông góc với đường thẳng y = − x. 45 A. y = 45 x − 173; y = 45 x + 83. B. y = 45 x − 173. C. y = 45 x + 173; y = 45 x − 83. D. y = 45 x − 83. Câu 43: Hàm số y = x3 − 2 x 2 − 4 x + 2018 có đạo hàm là A. y = 3x 2 − 4 x + 2018 . B. y = 3x 2 − 2 x − 4 . C. y = 3x 2 − 4 x − 4 . D. y = x 2 − 4 x − 4 . Câu 44: Đạo hàm của hàm số y = − x3 + 3mx 2 + 3 (1 − m2 ) x + m3 − m2 (với m là tham số) bằng A. 3 x 2 − 6mx − 3 + 3m 2 . B. − x 2 + 3mx − 1 − 3m . C. −3 x 2 + 6mx + 1 − m 2 . D. −3 x 2 + 6mx + 3 − 3m 2 . 2x −1 Câu 45: Tính đạo hàm của hàm số y = . x+2 5 x+2 1 5 x+2 A. y = . . B. y = . . . ( 2 x − 1) 2x −1 2 ( 2 x − 1) 2x −1 2 2 1 x+2 1 5 x+2 C. y = . . D. y = . . . 2 2x −1 2 ( x + 2) 2 2x −1   Câu 46: Tính đạo hàm của hàm số y = sin  − 3x  . 6      A. y = 3cos  − 3 x  . B. y = −3cos  − 3x  . 6  6      C. y = cos  − 3x  . D. y = −3sin  − 3x  . 6  6  Câu 47: Cho hàm số y = log 3 (2 x + 1) , ta có: 1 1 A. y = . B. y = . 2x +1 (2 x + 1) ln 3 2 2 C. y = . D. y = . (2 x + 1) ln 3 2x +1
1 Câu 48: Đạo hàm của hàm số y = là: log 2 x ln 2 ln 2 A. y ' = − . B. y ' = . x ln 2 x x ln 2 x x ln 2 x ln 2 C. y ' = − . D. y ' = . log 2 x 2 log 2 x 2 Câu 49: Đạo hàm của hàm số y = ( 2 x + 1) ln (1 − x ) là. 2x +1 A. 2 ln (1 − x ) − . B. 2 x ln ( x − 1) . 1− x 2x +1 2x +1 C. + 2x . D. 2 ln (1 − x ) + . 1− x 1− x Câu 50: Hàm số y = 8x + x +1 ( 6 x + 3) ln 2 là đạo hàm của hàm số nào sau đây? 2 + x +1 + x +1 A. y = 8x B. y = 2 x 2 2 + 3 x +1 + 3 x +1 C. y = 23 x D. y = 83 x 2 2 Câu 51: Cho hàm số y = x − 3 x + x + 1 với x  . Đạo hàm y của hàm số là 5 4 A. y = 5 x − 12 x + 1 . B. y = 5 x − 12 x . 3 2 4 3 C. y = 20 x − 36 x . D. y = 20 x − 36 x . 2 3 3 2 1 Câu 52: Tính đạo hàm của hàm số y = . x2 + 1 x x A. y = . B. y = − . ( x 2 + 1) x 2 + 1 ( x 2 + 1) x 2 + 1 x x( x 2 + 1) C. y = . D. y = − . 2( x 2 + 1) x 2 + 1 x2 + 1 1 Câu 53: Hàm số y = ln . Hệ thức nào sau đây đúng? x A. e y + y ' = 0 B. e y − y ' = 0 1 C. e y . y ' = 0 D. e y . y ' = x2  x −1  Câu 54: Đạo hàm của hàm số y = log 2   là:  ln x  x ln x + 1 − x x ln x + 1 − x A. . B. . x ( x − 1) ln 2 ( x − 1) ln x ln 2 x ln x + 1 − x x ln x + 1 − x C. . D. . ( x − 1) ln 2 x ( x − 1) ln 2.ln x Câu 55: Cho f ( x ) = 2 x 2 − x + 2 và g ( x ) = f ( sin x ) . Tính đạo hàm của hàm số g ( x ) . A. g  ( x ) = 2 cos 2 x − sin x. B. g  ( x ) = 2sin 2 x + cos x. C. g  ( x ) = 2sin 2 x − cos x. D. g / ( x ) = 2 cos 2 x + sin x.
cos 2 x Câu 56: Tính đạo hàm của hàm số y = . 3x + 1 −2 ( 3x + 1) sin 2 x − 3cos 2 x −2 ( 3x + 1) sin 2 x − 3cos 2 x A. y = . B. y = . ( 3x + 1) 3x + 1 2 − ( 3x + 1) sin 2 x − 3cos 2 x 2 ( 3x + 1) sin 2 x + 3cos 2 x C. y = . D. y = . ( 3x + 1) ( 3x + 1) 2 2 Câu 57: Tính đạo hàm của hàm số y = 2sin 2 x − cos 2 x + x . A. y = 4sin x + sin 2 x + 1. B. y = 4sin 2 x + 1. C. y = 4 cos x + 2sin 2 x + 1. D. y = 4sin x − 2sin 2 x + 1.  Câu 58: Đạo hàm cấp hai của hàm số y = −3cos x tại điểm x0 = . 2     A. y   = −3 . B. y   = 5 . 2 2     C. y   = 0 . D. y   = 3 . 2 2 Câu 59: Cho hàm số f ( x ) = ( x + 1) . Tính f  ( 2 ) . 4 A. 27. B. 81. C. 96. D. 108. Câu 60: Cho hàm số f ( x ) = ( 3x − 7 ) . Tính f  ( 2 ) . 5 A. f  ( 2 ) = 0 . B. f  ( 2 ) = 20 . C. f  ( 2 ) = − 180 . D. f  ( 2 ) = 30 . Câu 61: Cho hàm số y = sin 2 x . Khi đó y ''( x ) bằng 1 A. y '' = cos 2 x . B. P = 2sin 2 x . 2 C. y '' = 2 cos 2 x . D. y '' = 2 cos x . 1 Câu 62: Cho hàm số y = − . Đạo hàm cấp hai của hàm số là x 2 −2 A. y ( ) = 3 . B. y ( ) = 2 . 2 2 x x −2 2 C. y ( ) = 3 . D. y ( ) = 2 . 2 2 x x 2 Câu 63: Cho hàm số y = cos x. Tính y ? A. y = −2 cos2x. B. y = −4 cos2x. C. y = 2 cos2x. D. y = 4 cos2x. Câu 64: Cho chuyển động thẳng xác định bởi phương trình S = t 3 − 3t 2 (t: tính bằng giây, s: tính bằng mét). Khẳng định nào sau đây là đúng? A. Vận tốc của chuyển động khi t = 3s là v = 12m / s. B. Vận tốc của chuyển động khi t = 3s là v = 24m / s. C. Gia tốc của chuyển động khi t = 4s là a = 18m / s2 . D. Gia tốc của chuyển động khi t = 4s là a = 9m / s2 .
Câu 65: Một chất điểm chuyển động thẳng xác định bởi phương trình: S = t 3 − 3t 2 + 5t + 2 , trong đó t tính bằng giây và S tính bằng mét. Gia tốc của chuyển động khi t = 3 là: ( ) A. 24 m / s2 . B. 17 m / s2 . ( ) C. 14 ( m / s ) . 2 D. 12 ( m / s ) . 2 PHÀN II. Câu trắc nghiệm đúng sai Câu 1: Một người vừa gieo một con xúc xắc để ghi lại số chấm xuất hiện, sau đó người này tiếp tục chọn ngẫu nhiên một lá bài từ bộ bài 52 lá. Các mệnh đề sau đúng hay sai? 1 a) Gọi A là biến cố: "Số chấm của xúc xắc lớn nhất", khi đó: P( A) = 6 3 b) Gọi B là biến cố: "Chọn được một lá K", khi đó: P( B) = 13 c) Xác suất để số chấm trên con xúc xắc là lớn nhất và chọn được một lá K 1 bằng: 78 1 d)Xác suất để số chấm trên con xúc xắc và số của lá bài là giống nhau bằng: 16 1 1 Câu 2: Cho A, B là hai biến cố độc lập và P( A) = , P( B) = . Khi đó: 4 3 Các mệnh đề sau đúng hay sai? 1 a) P( AB) = 2 1 b) P( AB ) = 16 1 c) P( AB ) = 2 1 d) P( AB) = 4 1 Câu 3: Cho các biểu thức A = 2  3 2  4 2 , B = 24 25  . Các mệnh đề sau đúng hay sai? 2−1 a a a) A = 2 b ( là phân số tối giản), khi đó: a + b = 41 b a a b) B = 2 b ( là phân số tối giản), khi đó: a + b = 31 b c) A − B 5 = 5 m m d) A.B = 2 n ( là phân số tối giản), khi đó: m + n = 29 n 5 +2  a 5  a −2− 5 Câu 4: Cho biểu thức A =  5 − 2   −1 với a, b  0 . Các mệnh đề sau đúng hay sai? b  b   a) Sau khi rút gọn, thì biểu thức A chỉ chứa biến b
113 b) Với a = 2, b = 1 + 5 2 thì A = 3 c) Khi A = a m .b n thì m + n = 3 + 5 d) Khi A = a m .b n thì m − n = 2 + 5 1 Câu 5: Cho các số a, b, c là các số thực dương, khác 1 thỏa mãn: log a 3 = 2 , log b 3 = và 4 2 log abc 3 = . Các mệnh đề sau đúng hay sai? 15 a) a =  3 . b) b = a 8 . 3 c) log a2 ( ab ) = . 4 1 d) log c 3 = . 3  b3  log a ( a 3b 2 ) − log b  2  Câu 6: Cho các biểu thức sau: P =  a  và Q = log b3 + log b 6 với a, b log a b + 1 a2 2 a là các số dương và a khác 1. Vậy: a) Q = 6 log a b b) P = 6 log b a c) Q = 3P d) Q.P = 12 Câu 7: Cho hàm số y = log 4 x a)Hàm số có tập xác định D = b)Hàm số đồng biến trên khoảng ( 0; + ) 1  c)Hàm số đi qua điểm A  ; −1 4  d)Đồ thị hàm số cắt đường thẳng y = 1 tại điểm có hoành độ bằng 3 Câu 8: Cho hàm số y = 2 x a)Hàm số có tập xác định D = . b)Hàm số nghịch biến trên khoảng ( −; + ) c)Đồ thị hàm số đi qua điểm A ( 2; 4 )
d)Đồ thị hàm số có dạng như sau: Câu 9: Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hoá và dịch vụ theo thời gian, tức là sự mất giá trị của một loại tiền tệ nào đó. Chẳng hạn, nếu lạm phát là 5% một năm thì sức mua của 1 triệu đồng sau một năm chỉ còn là 950 nghìn đồng (vì đã giảm mất 5% của 1 triệu đồng, tức là 50000 đồng). Nói chung, nếu tỉ lệ lạm phát trung bình là r % một năm n  r  thì tổng số tiền P ban đầu, sau n năm số tiền đó chỉ còn giá trị là: A = P 1 −   100  a) Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 86490000 đồng. b) Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại 96490000 đồng. c) Nếu sức mua của 100 triệu đồng sau ba năm chỉ còn lại 80 triệu đồng thì tỉ lệ lạm phát trung bình của ba năm đó là 9,17% (làm tròn kết quả đến hàng phần trăm)? d) Nếu tỉ lệ lạm phát trung bình là 6% một năm thì sau 15 năm sức mua của số tiền ban đầu chỉ còn lại một nửa. Câu 10: Cho phương trình log 3 ( x + 6) = log 3 ( x − 1) + 1 (*). Khi đó: a) Điều kiện: x  1 x 2 − 11x + 9 b) Phương trình (*) có chung tập nghiệm với phương trình =0 x −1 5 c) Gọi x = a là nghiệm của phương trình (*), khi đó lim ( x − 3) = x →a 2 d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng: d1 : 2 x − y − 8 = 0 với d 2 : y = 0 . Câu 11: Cho hàm số y = f ( x) = 2 x 3 có đồ thị (C ) và điểm M thuộc (C ) có hoành độ x0 = −1 . Khi đó: a) Hệ số góc của tiếp tuyến của (C ) tại điểm M bằng 6 b) Phương trình tiếp tuyến của (C ) tại M đi qua điểm A ( 0; 4 ) c) Phương trình tiếp tuyến của (C ) tại M cắt đường thẳng d : y = 3x tại điểm có hoành độ bằng 4
1 d) Phương trình tiếp tuyến của (C ) tại M vuông góc với đường thẳng  : y = − x 6 2 Câu 12: Cho hàm số f ( x) = có đồ thị (C ) và điểm M (3; −1)  (C ) . Khi đó: 1− x 1 a) Hệ số góc của tiếp tuyến của (C ) tại điểm M bằng 2 1 5 b) Phương trình tiếp tuyến của (C ) tại M song song với đường thẳng y = − x − 2 2 5 c) Phương trình tiếp tuyến của (C ) tại M vuông với đường thẳng y = −2 x − 2  5 d) Phương trình tiếp tuyến của (C ) tại M đi qua điểm A  0; −   2 x2 Câu 13: Cho hàm số y = −4 x3 + − 2 x + 3 , biết y ' = ax 2 + bx + c . Khi đó: 2 a) a + b + c = −10 b) Phương trình y ' = 0 có hai nghiệm phân biệt c) Đồ thị hàm số y ' cắt trục tung tại điểm ( 0; −2 ) d) Đồ thị hàm số y ' cắt đường thẳng y = 3 tại hai điểm phân biệt Câu 14: Cho vật M chuyển động thẳng xác định bởi phương trình s (t ) 2t 3 3t 2 4t , trong đó t được tính bằng giây và s được tính bằng mét. a) Sau 2 giây vật M di chuyển được 12m. b) Vận tốc tức thời được xác định bởi phương trình v(t ) 6t 2 6t 4 (m/s). c) Gia tốc của vật tại thời điểm 1 giây là 8 m / s 2 . d) Vận tốc tức thời của vật tại thời điểm gia tốc bằng không là 2,5m / s. PHẦN III. Câu trắc nghiệm trả lời ngắn Câu 1: Người ta thăm dò một số lượng người hâm mộ bóng đá tại một thành phố, nơi có hai đội bóng đá X và Y cùng thi đấu giải vô địch quốc gia. Biết rằng số lượng người hâm mộ đội bóng đá X là 22% , số lượng người hâm mộ đội bóng đá Y là 39% , trong số đó có 7% người nói rằng họ hâm mộ cả hai đội bóng trên. Chọn ngẫu nhiên một người hâm mộ trong số những người được hỏi, tính xác suất để chọn được người không hâm mộ đội nào trong hai đội bóng đá X và Y . Trả lời: Câu 2: Một đề thi trắc nghiệm gồm 50 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng, mỗi câu trả lời đúng được 0,2 điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên 1 trong 4 phương án ở mỗi câu. Tính xác suất để thí sinh đó được 6 điểm. Trả lời: 1 1 a3 b + b3 a Câu 3: Cho hai số thực dương a, b . Rút gọn biểu thức A = 6 , ta được A = a m .b n . a+ b6 Tính S = 3m + 6n . Trả lời: Câu 4: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức s (t ) = s (0)  2t , trong đó s (0) là số lượng vi khuẩn A lúc ban đầu, s (t ) là số lượng vi khuẩn
A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? Trả lời: Câu 5: Cho log a b = 2 và log a c = 3 . Tính Q = log a ( b 2 c 3 ) . Trả lời: Câu 6: Cho a, b  0 và đều khác 1 thoả mãn ln a + ln(8b) = 2 ln( a + 2b) . 1 Rút gọn biểu thức: P = logb (2a) + log a (2b) − . 2 log8 b Trả lời: Câu 7: Các nhà tâm lí học sử dụng mô hình hàm số mũ để mô phỏng quá trình học tập của một học sinh như sau: y f (t ) c(1 e kt ) , trong đó c là tổng số đơn vị kiến thức học sinh phải học, k (kiến thức /ngày) là tốc độ tiếp thu của học sinh, t (ngày) là thời gian học và f (t ) là số đơn vị kiến thức học sinh đã học được. Giả sử một em học sinh phải tiếp thu 30 đơn vị kiến thức mới. biết rằng tốc độ tiếp thu của em học sinh là 0,2. Hỏi em học sinh sẽ học được bao nhiêu đơn vị kiến thức mới sau 6 ngày? (làm tròn kết quả đến hàng đơn vị) Trả lời: Câu 8: Ông An gửi 100 triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất 6% /năm. Giả sử qua các năm thì lãi suất không thay đổi và ông An không gửi thêm tiền. Để biết sau y (năm ) thì tổng số tiền cả gốc lẫn lãi có được x (đồng), ông An sử x dung công thức y log1,06 ( ) . Hỏi sau ít nhất bao nhiêu năm thì ông An có thể rút ra được 100 200 triệu đồng. Trả lời: 1 Câu 9 : Biết phương trình tiếp tuyến của đường cong y = có hệ số góc của tiếp tuyến bằng x 1 − là ax by 4 0. Hãy tính a 2 b2 ? 4 Trả lời: Câu 10: Một viên đạn được bắn lên cao theo phương trình s ( t ) = 196t − 4,9t 2 trong đó t  0, t tính bằng giây kể từ thời điểm viên đạn được bắn lên cao và s ( t ) là khoảng cách của viên đạn so với mặt đất được tính bằng mét. Tại thời điểm vận tốc của viên đạn bằng 0 thì viên đạn cách mặt đất bao nhiêu mét? Trả lời: 1 Câu 11: Một chất điểm chuyển động thẳng xác định bởi phương trình s(t ) = t 2 , trong đó t 2 là thời gian tính bằng giây và s là quãng đường đi được trong t giây tính bằng mét. Tính vận tốc tức thời của chất điểm tại t = 5 . Trả lời: Câu 12: Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m . Độ dốc của mặt cầu không vượt quá 10 (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chũ số thập phân thứ nhất).
Trả lời: x−3 2 Câu 13: Cho hàm số y = . Tính M = 2 ( y ) + (1 − y ) .y. x+4 Trả lời: Câu 14: Cho hàm số y = sin 2 x − cos 2 x . Phương trình y = 0 có nghiệm dương nhỏ nhất là a b . Hãy tính a 2 b 2 . 8 Trả lời: B. HÌNH HỌC PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn Câu 1: Cho hình lập phương ABCD. A ' B ' C ' D '. Tính góc giữa hai đường thẳng AC và A ' B. A. 60 B. 45 C. 75 D. 90 Câu 2: Cho hình lập phương ABCD. ABC D . Góc giữa hai đường thẳng BA và CD bằng: A. 45 . B. 60 . C. 30 . D. 90 . Câu 3: Cho hình lập phương ABCD. ABC D . Góc giữa hai đường thẳng AC  và BD bằng. A. 60 . B. 30 . C. 45 . D. 90 . Câu 4: Cho hình lăng trụ đều ABC. ABC  có cạnh đáy bằng 1 , cạnh bên bằng 2 . Gọi C1 là trung điểm của CC  . Tính côsin của góc giữa hai đường thẳng BC1 và AB . A. 2. B. 2 . C. 2 . D. 2 . 6 4 3 8 Câu 5: Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật với AB = 2a , BC = a . Các cạnh bên của hình chóp cùng bằng a 2 . Tính góc giữa hai đường thẳng AB và SC . A. 45 . B. 30 . C. 60 . D. arctan 2 . Câu 6: Cho tứ diện đều ABCD . Số đo góc giữa hai đường thẳng AB và CD là A. 45 . B. 90 . C. 60 . D. 30 . Câu 7: Cho hình chóp S . ABCD có đáy là hình bình hành tâm O , SA = SC , SB = SD . Trong các khẳng định sau khẳng định nào đúng? A. SA ⊥ ( ABCD ) . B. SO ⊥ ( ABCD ) . C. SC ⊥ ( ABCD ) . D. SB ⊥ ( ABCD ) . Câu 8: Cho hình chóp S . ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy ( ABCD ) . Khẳng định nào sau đây sai?
A. CD ⊥ ( SBC ) . B. SA ⊥ ( ABC ) . C. BC ⊥ ( SAB ) . D. BD ⊥ ( SAC ) . Câu 9: tứ diện ABCD có hai mặt ABC và ABD là hai tam giác đều. Gọi M là trung điểm của AB . Khẳng định nào sau đây đúng? A. CM ⊥ ( ABD ) . B. AB ⊥ ( MCD ) . C. AB ⊥ ( BCD ) . D. DM ⊥ ( ABC ) . Câu 10: Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật tâm I , cạnh bên SA vuông góc với đáy. Gọi H , K lần lượt là hình chiếu của A lên SC , SD . Khẳng định nào sau đây đúng? A. AH ⊥ ( SCD ) . B. BD ⊥ ( SAC ) . C. AK ⊥ ( SCD ) . D. BC ⊥ ( SAC ) . Câu 11: Cho hình chóp S . ABCD có đáy ABCD là hình vuông, SA ⊥ ( ABCD ) . Gọi M là hình chiếu của A trên SB . Khẳng định nào sau đây là đúng? A. AM ⊥ SD . B. AM ⊥ ( SCD ) . C. AM ⊥ CD . D. AM ⊥ ( SBC ) . Câu 12: Cho hình chóp SABC có SA ⊥ ( ABC ) . Gọi H , K lần lượt là trực tâm các tam giác SBC và ABC . Mệnh đề nào sai trong các mệnh đề sau? A. BC ⊥ ( SAH ) . B. HK ⊥ ( SBC ) . C. BC ⊥ ( SAB ) . D. SH , AK và BC đồng quy. Câu 13: Cho hình chóp S . ABC có SA ⊥ ( ABC ) ; tam giác ABC đều cạnh a và SA = a (tham khảo hình vẽ bên). Tìm góc giữa đường thẳng SC và mặt phẳng ( ABC ) . S A C B o o A. 60 . B. 45 . C. 135o . D. 90o . Câu 14: Cho hình chóp S . ABC có cạnh SA vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng đáy là góc giữa hai đường thẳng nào dưới đây? A. SB và AB . B. SB và SC . C. SA và SB . D. SB và BC . Câu 15: Cho hình lăng trụ đều ABC. ABC  có AB = 3 và AA = 1 . Góc tạo bởi giữa đường thẳng AC  và ( ABC ) bằng A. 45o . B. 60o . C. 30o . D. 75o . Câu 16: Cho khối chóp S . ABCD có đáy ABCD là hình vuông cạnh a , Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích của khối a 3 15 chóp S . ABCD là . Góc giữa đường thẳng SC và mặt phẳng đáy ( ABCD ) 6 là
A. 120o . B. 30o . C. 45o . D. 60o . Câu 17: Cho hình lập phương ABCD. ABC D . Số góc phẳng nhị diện [ B, AC , A '] bằng: A. 45 . B. 60 . C. 30 . D. 90 . Câu 18: Cho hình lập phương ABCD. ABC D . Góc giữa ( ABCD ) và ( ABC D ) bằng A. 45 . B. 60 . C. 0 . D. 90 . Câu 19: Cho hai mặt phẳng P và Q song song với nhau và một điểm M không thuộc P và Q . Qua M có bao nhiêu mặt phẳng vuông góc với P và Q ? A. 2. B. 3. C. 1. D. Vô số. Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng? A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c a, c b . Mọi mặt phẳng chứa c thì đều vuông góc với mặt phẳng a, b B. Cho a , mọi mặt phẳng chứa a thì . C. Cho a b , mọi mặt phẳng chứa b đều vuông góc với a . D. Cho a b , nếu a và b thì . Câu 21: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với đáy. Gọi M là trung điểm AC . Khẳng định nào sau đây sai? A. BM AC. B. SBM SAC . C. SAB SBC . D. SAB SAC . Câu 22: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , mặt bên SAC là tam giác đều và mằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC . Mệnh đề nào sau đây sai? A. AI SC . B. SBC SAC . C. AI BC. D. ABI SBC . Câu 23: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Cạnh bên SA a 3 và vuông góc với mặt đáy ABC . Gọi là góc nhị diện SBC và ABC . Mệnh đề nào sau đây đúng? 30 0. 5 A. B. sin . 5 60 0. 2 5 C. D. sin . 5 Câu 24: Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D , AB 2 a, AD CD a . Cạnh bên SA a và vuông góc với mặt phẳng ABCD . Gọi là góc giữa hai mặt phẳng SBC và ABCD . Mệnh đề nào sau đây đúng? 2 450. 60 0. 30 0. A. tan . B. C. D. 2 Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1 . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy ABCD . Tính khoảng cách d từ A đến SCD . A. d 1 . B. d 2. 2 3 21 C. d . D. d . 3 7 Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a . Cạnh bên SA a 2 và vuông góc với đáy ABCD . Tính khoảng cách d từ điểm B đến mặt phẳng SCD .
a 6 A. d a. B. d . 3 a 3 C. d a 3. D. d . 2 Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a. Cạnh bên a 15 SA và vuông góc với mặt đáy ABCD . Tính khoảng cách d từ O đến mặt 2 phẳng SBC . a 285 285 A. d . B. d . 19 38 a 285 a 2 C. d . D. d . 38 2 Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 60 . Tính khoảng cách d từ điểm D đến mặt phẳng SBC . a 3 3 A. d . B. d . C. d a. D. d a 3. 2 2 Câu 29: Cho hình chóp S . ABC có đáy ABC là tam giác đều cạnh a , SA ⊥ ( ABC ) , 3 SA = a . Gọi ( P ) là mặt phẳng đi qua A và vuông góc với trung tuyến SM của 2 tam giác SBC . Diện tích của hình tạo bởi các đoạn giao tuyến của ( P ) và các mặt của hình chóp S . ABCD bằng? a2 6 a2 a2 6 A. . B. . C. a 2 . D. . 8 6 16 Câu 30: Cho hình chóp S . ABCD với ABCD là hình chữ nhật có AB = a , AD = 2a . SA vuông góc với đáy và SA = a . Gọi ( P ) là mặt phẳng qua SO và vuông góc với ( SAD ) . Diện tích của hình tạo bởi các đoạn giao tuyến của ( P) và các mặt của hình chóp S . ABCD bằng? 3 2 a2 A. a 2 . B. a 2 . C. . D. a 2 2 2 2 Câu 31: Cho hình chóp S . ABCD có đáy là hình chữ nhật, các mặt ( SAB ) , ( SAD ) vuông góc với đáy. Góc giữa ( SCD ) và đáy bằng 60 , BC = a . Khoảng cách giữa hai đường thẳng AB và SC bằng 3a 3 a 3 A. . B. 2 a. C. . D. 2 a. 2 13 2 5 Câu 32: Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA = a 2. Tính thể tích V của khối chóp S . ABCD. a3 2 a3 2 A. V . B. V . 6 4 a3 2 C. V a 3 2. D. V . 3 Câu 33: Cho khối chóp S.ABC có SA vuông góc với đáy, SA 4, AB 6, BC 10 và CA 8 . Tính thể tích V của khối chóp S.ABC .
A. V 40. B. V 192. C. V 32. D. V 24. Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB a , BC 2a . Hai mặt bên SAB và SAD cùng vuông góc với mặt phẳng đáy ABCD , cạnh SA a 15 . Tính theo a thể tích V của khối chóp S.ABCD. 2a 3 15 2a 3 15 A. V . B. V . 6 3 a 3 15 C. V 2a 3 15 . D. V 3 Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình vuông bên SA vuông góc cạnh a . Cạnh với đáy ABCD và SC a 5 . Tính theo a thể tích V khối chóp S.ABCD. a3 3 a3 3 A. V . B. V . 3 6 a 3 15 C. V a3 3 . D. V . 3 PHẦN II. Câu trắc nghiệm đúng sai Câu 1: Trong không gian, cho ba đường thẳng phân biệt a, b, c . Xác định tính đúng sai các mệnh đề sau? a) Nếu a / / b thì (a, c) = (c, b) . b) Nếu c / / b thì (a, b) = (a, c) . c) Nếu a ⊥ c, b ⊥ c thì a / / b . d) Nếu a ⊥ c thì (a, b) = (c, b) . Câu 2: Cho hình chóp S . ABC có SA ⊥ ( ABC ) và tam giác ABC vuông tại B . Gọi H , K là hình chiếu vuông góc của A trên các cạnh SB, SC . Khi đó: a) Tam giác SBC cân tại B . b) AH vuông góc với mặt phẳng ( SBC ) . c) ( SC , HK ) = 90 d) Giả sử HK cắt BC tại D . Khi đó ( AC , AD ) = 90 . Câu 3: Cho tứ diện ABCD có AB, AC , AD đôi một vuông góc với nhau. Biết rằng AB = AC = a, AD = a 3 . a) AC ⊥ ( ABD ) d) (CD, ( ABD)) = 30 c) Góc phẳng nhị diện [ A, BC , D]  87, 79 d) Góc phẳng nhị diện [C , AB, D ] = 90 Câu 4: Cho lăng trụ đứng ABC  A BC  có đáy là tam giác vuông tại A , biết AB = a , ( AC = a 3 và ( ACB ) , ( ABC ) = 60 . Khi đó: )  a) A A ⊥ ( ABC ) b) (( ACB ) , ( ABB A )) = 60 .    c) ( ( ACC A ) , ( BCC B ) ) = 30      d) Tổng diện tích ba mặt bên của hình lăng trụ đã cho bằng (3 3 + 3)a 2
Câu 5: Cho hình chóp đều S . ABC có cạnh đáy bằng a , gọi O là tâm của đáy và a 3 SO = . Khi đó: 3 a 3 a) AO = 2 a 6 b) d (O, SA) = . 6 a 3 c) Kẻ đường cao AI của tam giác ABC , khi đó: OI = 6 a 15 d) d (O, ( SBC )) = 12 Câu 6: Cho hình chóp S . ABC có mặt bên ( SAB ) vuông góc với mặt đáy và tam giác SAB đều cạnh 2a . Biết tam giác ABC vuông tại C và cạnh AC = a 3 . Khi đó: a) SH ⊥ ( ABC ) b) d ( S , ( ABC )) = a 3 a 3 c) d (C , ( SAB)) = 3 a3 d) Thể tích của khối chóp S . ABC bằng 6 PHẦN III. Câu trắc nghiệm trả lời ngắn Câu 1: Cho tứ diện đều ABCD có cạnh 2a . Tìm đoạn vuông góc chung của hai đường thẳng chéo nhau AB, CD và tính độ dài của nó theo a . Trả lời: Câu 2: Cho hình chóp S . ABCD có cạnh bên SA ⊥ ( ABC ) và đáy ABC là tam giác cân ở B . Gọi H và K lần lượt là trung điểm của AC và SC . Xác định góc của hai đường thẳng BH , SC . Trả lời: Câu 3: Kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m . Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy của kim tự tháp đó. Trả lời: Câu 4: Kim tự tháp Kheops - Ai Cập có dạng hình chóp đều, đáy là hình vuông, mỗi cạnh bên của kim tự tháp dài 214 m , cạnh đáy của nó dài 230 m . Tìm góc giữa mặt bên và mặt đáy của kim tự tháp (tính theo độ, kết quả được làm trong đến hàng phần chục).
Câu 5: Cho hình chóp S . ABCD có đáy là hình vuông cạnh a , hai mặt phẳng ( SAB ) và ( SBC ) cùng vuông góc với mặt phẳng ( ABCD ) và SC = a 5 . Tính khoảng cách từ D đến mặt phẳng ( SAC ) . Trả lời: Câu 6: Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng 30 cm , hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ chơi được làm bởi chất liệu nhựa đặc bên trong). Trả lời: