PHÒNG GD&ĐTPHÚC YÊN
ĐỀ KHẢO SÁT LẦN 1
MÔN: TOÁN 9
Năm học 2011 - 2012
Thời gian: 120 phút (Không kể thời gian giao đề)
I. Phần trắc nghiệm.
Viết vào bài làm chữ cái trước những câu trả lời mà em chọn là kết quả đúng.
Câu 1. Điều kiện xác định của biểu thức
32 x
là:
A.
3
x2
B.
3
x2
C.
3
x2
D.
3
x2
Câu 2. Tính
2
)31(
được kết quả là:
A.
13
B.
)31(
C.
31
D. 2
Câu 3. Cho tam giác ABC vuông ở A, biết BC = 13; AB = 12 giá trị của sinB là:
A.
. B.
. C.
. D.
.
Câu 4. Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sau đây sai ?
A. BC.AH = AB.AC B. AH2 = AB2+AC2
C. AC2 = BC.CH D. AH2 = BH.CH
II. Phần tự luận.
Câu 5. Tính:
a)
22
5 2 2 5
b) Tính giá trị của biểu thức M =
14416 2 aaa
tại a = -0,25
Câu 6. Tìm x biết
2
x 3x 2 x 2
Câu 7. Cho biểu thức A =
2
1
1
:
1
11
x
x
xxx
a) Tìm tập xác định và rút biểu thức A
b) Tim giá trị của x để A >
3
1
.
c) Tìm giá trị lớn nhất của biểu thức P = A - 9
x
Câu 8. Cho ABC vuông tại A, đường cao AH; HB = 3,6cm; HC = 6,4cm.
a) Tính độ dài các đoạn thẳng: AB, AC, AH.
b) Kẻ HE
AB; HF
AC. Tính diện tích tứ giác BEFC.
c) Kẻ phân giác AD (D
BC), chứng minh
1 1 2
AB AC AD

Câu 9. Tìm GTLN và GTNN của biểu thức sau:
2
2
x x 1
Ax x 1


------------ Hết ------------
Họ và tên:…………………….…………..SBD:……………….
PHÒNG GD&ĐTPHÚC YÊN
HƯỚNG DẪN CHẤM KHẢO SÁT
MÔN: TOÁN 9
Năm học 2011 - 2012
I. Phần trắc nghiệm. (2đ) Mỗi câu đúng cho 0,5 điểm
Câu
1
2
3
4
Đáp án
D
A
C
B
II. Phần tự luận.
Câu
Ý
Nọi dung cần đạt
Điểm
Câu
5
a
1đ
5 2 2 5
5 2 ( 5 2)
5 2 5 2
22
0,25
0,25
0,25
0,25
b
1đ
Tính được kết quả M = 0,5
Học sinh có thể đơn giản biểu thức rồi tính hoặc thay a vào biểu thức sau
đó tính.
1đ
Câu
6
1đ
2
x 3x 2 x 2
2
2
x 2 0
x 3x 2 x 2

x2
x6
x = 6. Vậy x = 6 là giá trị cần tìm.
0,5đ
0,5đ
Câu
7
a
Điều kiện xác định:
0; 1xx
Biến đổi được
2
1 1 1
:
11
x x x
Ax
xx x

0,75đ
b
Ta có A>
3
1









3 3 2 3
11 00
311
x x x
xxx
xxx
39
xx
24
9
x 0 x 0 x 4
x 1 x 1




 





. Vậy với
9
x4
thì A >
3
1
.
0,25
0,5
c
Với x>0 và x ≠ 1 ta có : P = A - 9
x
=
11
9 9 1
xxx
xx



Áp dụng bất đẳng thức Cô –si cho hai số dương ta có:
11
9 2 9 . 6xx
xx
=>
6 1 5P
. Đẳng thức xảy ra khi
11
99
xx
x
thỏa mãn điều kiện x>0 và x ≠ 1
Vậy giá trị lớn nhất của biểu thức
5P
khi
1
9
x
0,25
0,25
Câu
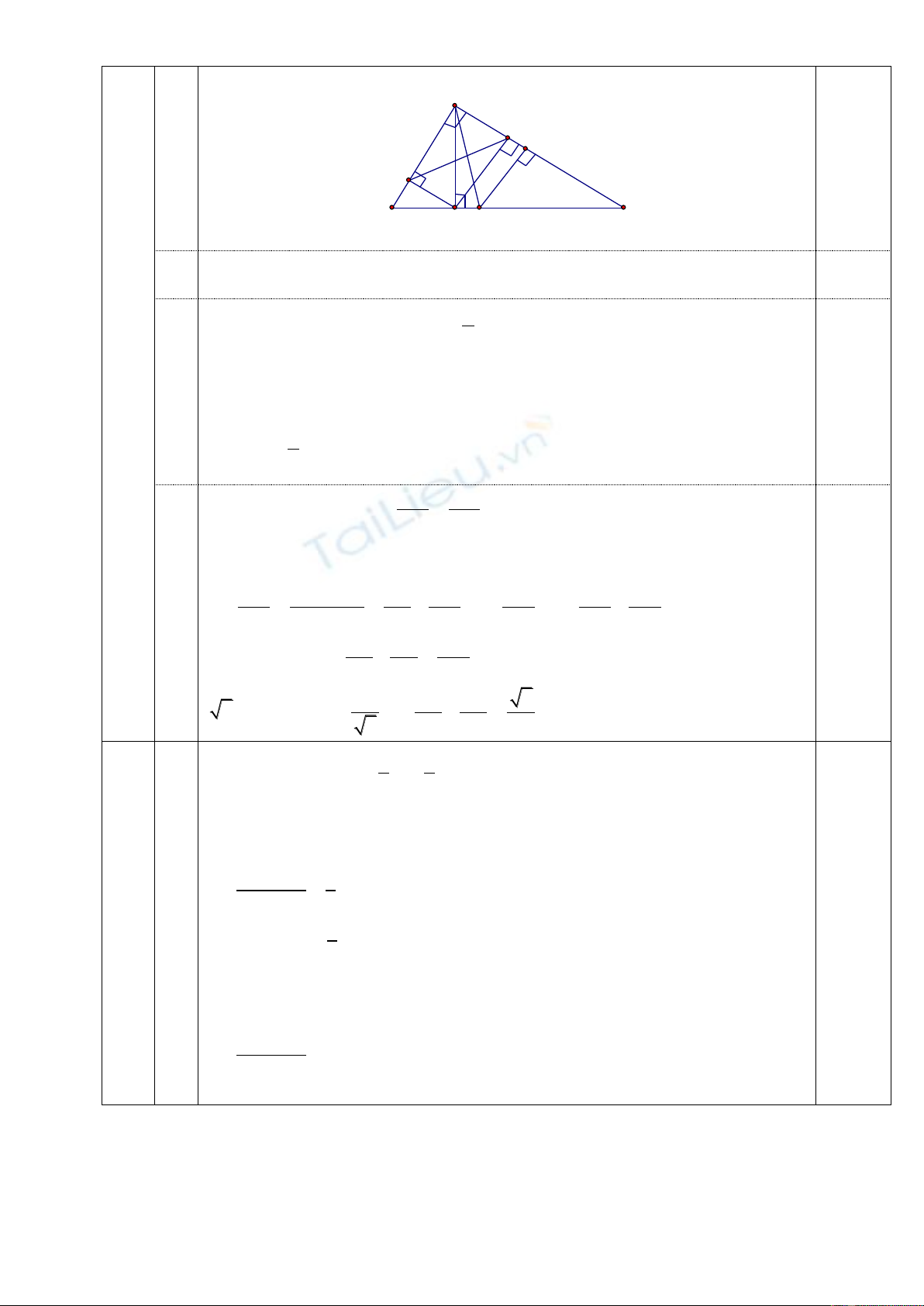
8
:
M
D
6,4
3,6
F
E
H
C
B
A
0,25
a
Áp dụng hệ thức thức lượng trong tam giác vuông ABC
Tính được AB = 6 cm; AC = 8cm; AH = 4,8 cm
0,5
b
BEFC ABC AEF
S S S
;
2
ABC 1
S .6.8 24 cm
2

Áp dụng hệ thức thức lượng trong các tam giác vuông ∆AHB và ∆AHC tính
được BE = 2,16 cm; FC = 5,12 cm
AE = 6 – 2,16 = 3,84 cm ; AF = 8 – 5,12 = 2,88 cm.
2
AEF 1
S .3,84.2,88 5,5296 cm
2

2
BEFC
S 24 5,5296 18,4704 cm
0,25
0,25
0,25
c
Từ D kẻ DM // AB ta có
DM CM
AB AC
Mà CM = AC – AM ; AM = DM ( ∆AMD vuông cân đỉnh M)
CM = AC – DM
DM AC DM AC DM DM
1
AB AC AC AC AC
DM DM 1
AB AC

. Chia cả hai vế
cho DM ta được
1 1 1
AB AC DM

Do ∆ADM vuông cân đỉnh M
AD =
2
DM
AD
DM 2
1 1 2
AB AC AD

(đpcm)
0,25
0,25
Câu
9
Ta có
2
213
x x 1 x 0
24



với
x. Vậy TXĐ của biểu thức A là
x
R..
Do
22
2
x 1 0 2. x 1 0 2x 4x 2 0
22
3. x x 1 x x 1
2
2
x x 1 1
x x 1 3



(1) (vì
2
x x 1 0
). Dấu "=" xảy ra tại x = -1
Vậy Min (A) =
1
3
tại x = -1.
- Ta lại có
22
2
x 1 0 2. x 1 0 2x 4x 2 0
22
3. x x 1 x x 1
2
2
x x 1 3
x x 1



(2) (vì
2
x x 1 0
). Dấu "=" xảy ra tại x = 1.
Vậy Max (A) = 3 tại x = 1.
0,5
0,5
Vẽ hình đúng, đẹp cho
TRƯỜNG THCS MẠC ĐĨNH CHI
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM LỚP 9
NĂM HỌC 2011 – 2012
Môn: Toán
Thời gian: 90 phút( Không kể thời gian giao đề)
ĐỀ BÀI
Câu 1: ( 1,5 điểm):
a)Phát biểu định nghĩa phương trình bậc nhất một ẩn? Cho ví dụ?
b)Áp dụng giải phương trình 2x-1= 0
Câu 2(2điểm) Giải các phương trình:
a) ( x - 3 ) - 2(3x - 2) = ( x +4 )
b) (x -
6
5
)(x +
2
1
) = 0
Câu 3(1điểm)Giải bất phương trỡnh
3 2 2
35
xx
và biểu diễn tập nghiệm trên trục số
Câu 4: (2điểm)Một đội máy kéo dự định mỗi ngày cày được 40 ha. Khi thực hiện, mỗi ngày
cày được 52 ha. Vỡ vậy, đội không những đó cày xong trước thời hạn 2 ngày mà cũn cày
thêm được 4 ha nữa. Tính diện tích ruộng mà đội phải cày theo kế hoạch đó định?
Câu 5( 3,5 điểm) Cho hỡnh chữ nhật ABCD cú AB = 8cm; BC = 6cm. Vẽ đường cao AH
của tam giác ABD
a) Chứng minh AHB BCD
b) Chứng minh AD2 = DH.DB
c) Tính độ dài đoạn thẳng DH và AH
Hướng dẫn chấm, thang điểm.
Câu
Đáp án
Điểm
1(2đ)
a)Phương trỡnh dạng ax+b=0, với a và b là hai số đó cho và a
0, được
gọi là phương trỡnh bậc nhất một ẩn
Ví dụ: 3x+ 2= 0
b) 2x-1= 0
2x = 1
x =
1
2
Vậy phương trỡnh cú tập nghiệm là: S =
1
2



0,25
0,25
0,25
0,25
2(2đ)
a) ( x - 3 ) - 2(3x - 2) = ( x +4 )
x – 3 - 6x + 4 = x + 4
- 6x = 3
x =
1
2
Vậy tập nghiệm phương trỡnh là S =
1
2



0,25
0,25
b) (x -
6
5
)(x +
2
1
) = 0
x =
6
5
hoặc x = -
2
1
0,5
3(1đ)





3 2 2
35
5 3 2 3 2
15 15
15 10 6 3
12 16
4
3
xx
xx
xx
x
x
Vậy tập nghiệm của bất phương trỡnh là:S=
4
/3
xx



0,25
0,25
0,25
0,25
4(2đ)
+ Gọi x là diện tích ruộng đội cày theo kế hoạch (ha; x > 40)
+ Diện tích ruộng đội đó cày được là: x + 4 (ha)
. Số ngày đội dự định cày là:
40
x
(ha)
. Số ngày đội đó cày là:
52
4x
(ha)
+ Đội cày xong trước thời hạn 2 ngày nên ta có phương trỡnh:
40
x
–
52
4x
= 2
+ Giải phương trỡnh được: x = 360
Đối chiếu và kết luận
0,25
0,25
0,25
0,25
0,25
0,5
0,25
0
4
3