Đề khảo sát đội tuyển Toán lớp 10 năm 2021-2022 có đáp án (Lần 2) - Trường THPT Trần Phú, Vĩnh Phúc

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

10
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mời các bạn tham khảo “Đề khảo sát đội tuyển Toán lớp 10 năm 2021-2022 có đáp án (Lần 2) - Trường THPT Trần Phú, Vĩnh Phúc” sau đây để hệ thống lại kiến thức đã học và biết được cấu trúc đề thi cũng như những nội dung chủ yếu được đề cập trong đề thi để từ đó có thể đề ra kế hoạch học tập và ôn thi một cách hiệu quả hơn. Chúc các bạn ôn tập thật tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề khảo sát đội tuyển Toán lớp 10 năm 2021-2022 có đáp án (Lần 2) - Trường THPT Trần Phú, Vĩnh Phúc

MA TRẬN ĐỀ KHẢO SÁT ĐỘI TUYỂN LẦN 2 TOÁN 10- NĂM HỌC 2021-2022 CẤP ĐỘ TƯ DUY TỔNG VẬN DỤNG NỘI DUNG NHẬN BiẾT THÔNG HiỂU VẬN DỤNG CAO TL TL TL TL Câu 1, câu 2 Hàm số 2 2 Câu 3 Hệ pt 1 ẩn 1 1 ĐẠI PT và HPT quy Câu 4a Câu 4b, câu 5 về bậc nhất , bâc 2 1 2 3 Câu 9 Bất đẳng thức 1 1 Vec tơ Câu 6 Câu 7 1 1 2 HÌNH Hệ thức lượng Câu 8 trong tam giác 1 1 Tổng 5 3 2
SỞ GD & ĐT VĨNH PHÚC ĐỀ KHẢO SÁT ĐỘI TUYỂN TOÁN LẦN 2 TRƯỜNG THPT TRẦN PHÚ Năm học: 2021 - 2022 Môn: Toán – Lớp 10 Thời gian làm bài: 180 phút, không kể thời gian phát đề Câu 1: (1 điểm) Cho Parabol  P  : y  x 2  2 x  2 và đường thẳng  d  : y  2 x  1 . Biết  P  và  d  cắt nhau tại hai điểm phân biệt A và B . Tính độ dài đoạn AB 1 Câu 2: (1 điểm) Tìm tập xác định của hàm số y  . 4 x  19 x  12 2  x 2  5 x  4  0 Câu 3: (1 điểm) Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm.  x  m  0 Câu 4: (2 điểm) a) Giải phương trình x 3 + x2 = x 2  3x  2 ìï x 2 + x3 y - xy 2 + xy - y = 1 b) Giải hệ phương trình: ïí 4 ïï x + y 2 - xy (2 x -1) = 1 î Câu 5: (1 điểm) Gọi x1 ; x2 là hai nghiệm của phương trình x 2  mx  m  1  0 . 4 x1 x 2  6 Đặt A  . Tìm giá trị của tham số m để A đạt giá trị nhỏ nhất. 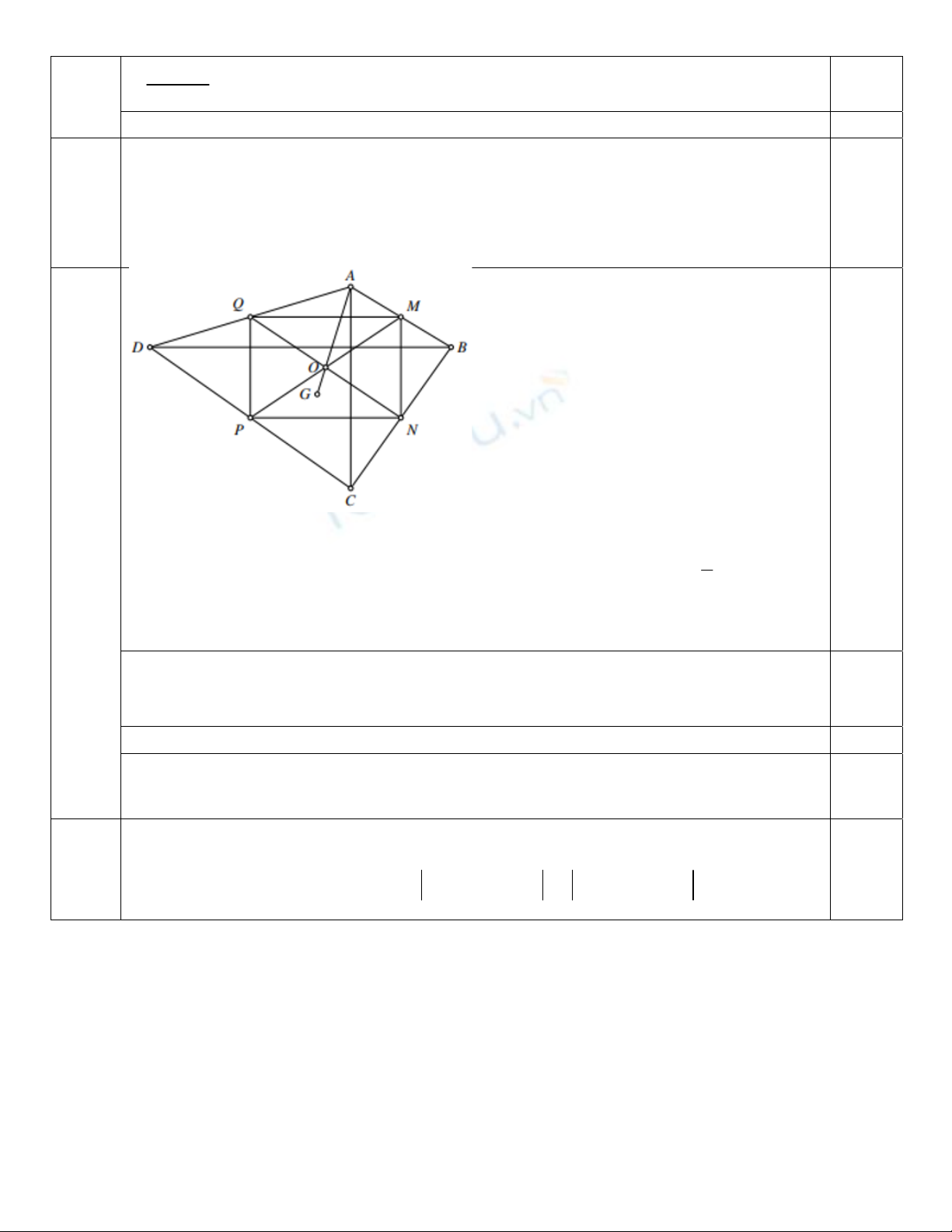x  x 22  2(1  x1 x 2 ) 2 1 Câu 6: (1 điểm) Cho tứ giác ABCD . Gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Gọi O là giao điểm của MP và NQ , G là trọng tâm của tam giác BCD . Chứng minh rằng ba điểm A , O , G thẳng hàng. Câu 7: (1 điểm) Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC .       Tìm giá trị nhỏ nhất của biểu thức T  MA  MB  MC  3 MA  MB  MC . Câu 8: (1 điểm) Cho tứ giác lồi ABCD có AC  BD và nội tiếp đường tròn tâm O bán kính R  1010 . Đặt diện tích tứ giác ABCD bằng S và AB  a, BC  b, CD  c, DA  d . Tính giá trị biểu thức T  ab  cd  ad  bc  . 4S Câu 9: (1 điểm) Cho x, y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức  x  1  x  1  2 A  y2   y2  y  2 ------------HẾT------------ Họ và tên thí sinh..................................................................................................SBD..........................................
SỞ GD & ĐT VĨNH PHÚC HƯỚNG DẪN CHẤM TRƯỜNG THPT TRẦN PHÚ ĐỀ KHẢO SÁT ĐỘI TUYỂN TOÁN LẦN 2 Năm học: 2021 - 2022 Môn: Toán – Lớp 10 (Hướng dẫn chấm gồm 6 trang) Câu Nội dung Điểm Câu 1 Cho Parabol  P  : y  x  2 x  2 và đường thẳng  d  : y  2 x  1 . Biết  P  và  d  cắt nhau 2 1 điểm tại hai điểm phân biệt A và B . Tính độ dài đoạn AB  x  1 Phương trình hoành độ giao điểm: x 2  2 x  2  2 x  1  x 2  4 x  3  0   0,5  x  3  A  1;1 ; B  3;5 . Ta có AB  2 5 0,5 Câu 2 1 Tìm tập xác định của hàm số y  . 1 điểm 4 x  19 x  12 2 x  4 1 Hàm số y  xác định khi và chỉ khi 4 x  19 x  12  0  2 4 x 2  19 x  12 x  3  4 0,5 x  4  3 0,5  3  D   ;    4;   x   4  4 Câu 3  x 2  5 x  4  0 Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm. 1 điểm  x  m  0  x 2  5 x  4  0 1  x  4 1 Ta có   0,5  x  m  0  x  m  2 Để hệ bất phương trình có nghiệm thì giao hai tập nghiệm của hai bất phương trình 1 ,  2  0,5 khác rỗng  m  4 Câu 4 a) Giải phương trình x 3 + x2 = x 2  3x  2 1 điểm Đk x  3 PT  x  3  x  2  2 x 2  5 x  6  x 2  3 x  2  x 2  5 x  6  2 x 2  5 x  6  3  0 0,25
Đặt t  x 2  5 x  6, t  0. Ta được pt : t 2  2t  3  0 0,25 t  1(l  t 2  2t  3  0   t  3(n) 0,25 t  3  x2  5x  6  3  x2  5x  3  0  5  37 x  (l ) 5  37 2 . KL pt có nghiệm là x   2 0,25  5  37 x  ( n)  2 ìï x 2 + x3 y - xy 2 + xy - y = 1 b)Giải hệ phương trình: ïí 4 1 điểm ïï x + y 2 - xy (2 x -1) = 1 î ì ï ï x 2 + x 3 y - xy 2 + xy - y = 1 (1) ì ï ï ï ( x 2 - y) + xy ( x 2 - y) + xy = 1 + Ta có: í 4 (*)  í 2 ï ï î x + y 2 - xy ( 2 x - 1) = 1 (2) ï ï( x - y ) 2 + xy = 1 ï î 0,25 ì ïïa = x 2 - y ìïa + ab + b = 1 + Đặt í . Hệ trở thành ïí 2 (**) ï îb = xy ï ïïîa + b = 1 ìa 3 + a 2 - 2 a = 0 ì ï ïïa (a 2 + a - 2) = 0 + Hệ (**)  ïí  í ïïb = 1- a 2 ï ïîb = 1- a 2 0,25 ï î Từ đó ta tìm ra (a; b) Î {(0; 1);(1; 0);(-2; -3)} ìï x 2 - y = 0 Với (a; b) = (0; 1) ta có hệ ïí  x = y =1 ïïî xy = 1 0,25 ìï x 2 - y = 1  Với (a; b) = (1; 0) ta có hệ ï í  ( x; y ) = (0; -1);(1; 0); (-1; 0) ïïî xy = 0 Với (a; b) = (-2; -3) ta có hệ   3  3  x 2  y  2 y   y   x   x   x  1; y  3 .  xy   3 x  2x  3  0 3 ( x  1)  x  x  3  0 2    0,25 Vậy hệ có 5 nghiệm  x; y  {1; 1 ;  0; 1 ; 1; 0 :  1; 0 ;  1; 3} . Câu 5 Gọi x1 ; x2 là hai nghiệm của phương trình x 2  mx  m  1  0 . 4 x1 x 2  6 Đặt A  . Với giá trị nào của m thì A đạt giá trị nhỏ nhất. x  x 22  2(1  x1 x 2 ) 2 1 + PT có hai ngiệm khi   0  m 2  4m  4  0, m ; x1  x2  m; x1 x 2  m  1 0,25 4 x1 x2  6 4m  2 A  2 ( x1  x2 )  2 m  2 2 0,25
(m  2) 2   1  1 0,25 m2  2 A nhỏ nhất khi m  2 0,25 Câu Cho tứ giác ABCD . Gọi M , N , P , Q lần lượt là trung điểm của AB , BC , CD , DA . Gọi 6 O là giao điểm của MP và NQ , G là trọng tâm của tam giác BCD . Chứng minh rằng ba điểm A , O , G thẳng hàng. 0,25  MN // PQ // AC  MN , PQ lần lượt là đường trung bình của ABC , ACD   1  MN  PQ  2 AC Do đó tứ giác MNPQ là hình bình hành  O là trung điểm của MP .                  Ta có: OA  OB  OC  OD  OM  MA  OM  MB  OP  PC  OP  PD      0,25    2 OM  OP  0 .     G là trọng tâm BCD  OB  OC  OD  3OG . 0,25           Khi đó: OA  OB  OC  OD  0  OA  3OG  0  OA   3OG . Vậy ba điểm A , O , G thẳng hàng (đpcm). 0,25 Câu Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC 7       1 điểm Tìm giá trị nhỏ nhất của biểu thức T  MA  MB  MC  3 MA  MB  MC .
0,25 Gọi G là trọng tâm ABC thì G cố định.   Vẽ CD  BA , vì ABC đều nên tứ giác ABCD là hình thoi và D cố định. Khi đó ta có          T  MA  MB  MC  3 MA  MB  MC  3 MG  3 BA  MC     3MG  3 CD  MC  3MG  3 MD  3  MG  MD   3GD. 0,25 Do MG không đổi nên T đạt giá trị nhỏ nhất bằng 3GD khi M , G , D thẳng hàng. Khi đó, M là trung điểm đoạn AC . 0,25 Giá trị nhỏ nhất của T là 1 4 4 a 3 2a 3 3GD  GM  MD  GM  MB  MB  MB  MB  .  . 0,25 3 3 3 2 3 Câu 8 Cho tứ giác lồi ABCD có AC  BD và nội tiếp đường tròn tâm O bán kính R  1010 . Đặt diện tích tứ giác ABCD bằng S và AB  a, BC  b, CD  c, DA  d . Tính giá trị biểu 1 điểm thức T   ab  cd  ad  bc  . 4S 0,25
a.b. AC S .4 R Ta có : S ABC   ab  ABC 4R AC S ADC .4 R S .4 R S .4 R Tương tự ta cũng có : cd  , ad  ABD , bc  BCD AC BD BD T  ab  cd  ad  bc  . 4S  S ABC .4 R S ADC .4 R  S ABD .4 R S BCD .4 R   AC  AC  BD  BD    . 0,25 4S 4 R 2  S ABC .S ABD  S ABC .S BCD  S ADC .S ABD  S ADC .S BCD   . S . AC.BD 4040  S ABC  S ABD  S BCD   S ADC  S ABD  S BCD    . 0,25 S . AC.BD 4040  S ABC .S  S ADC .S  4040 S  S ABC  S ADC  4040S .S     2020 . S . AC.BD S . AC.BD S .2S 0,25 Vậy T  2020 . Câu 9 Cho x, y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức 1 điểm  x  1  x  1  2 A y  2  y  y2 2  x  1  x  1 1  x  x  1   y  y  2 2 2 2 A  y2   y2  y  2   y2 0,25 Vậy A  4  4 y 2  y  2 TH1: y  2  A  2 1  y 2  2 5 0,25 TH2: y  2  A  2 1  y 2  2  y 0,25   3  2   12 12  y 2   2  y  3.1  1. y  2  y  3  2 1 A  2  3 khi và chỉ khi x  0, y  3 0,25 Ta có 2  3  2 5  min A  2  3 Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.