ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
Đề số 53
I. Phần trắc nghiệm: (3 điểm) Hãy khoanh vào câu đúng nhất:
Câu 1: Hai bán kính OA và OB của đường tròn (O) tạo thành góc AOB có số đo là
800, số đo của cung lớn AB là:
A. 1600 B. 2800 C. 800 D. 1200
Câu 2: Cho đường tròn (O) có hai điểm A, B nằm trên đường tròn sao cho số đo cung AB
bằng 360, số đo của góc AOB là:
A. 720 B. 180 C.360 D . Một kết quả khác
Câu 3: Góc BAC nội tiếp đường tròn (O), cung BC có số đo là 600. Vậy số đo của góc
BAC là:
A. 600 B.900 C. 300 D. 1200
Câu 4: Tứ giác ABCD nội tiếp đường tròn (O), có
0
ˆ
120
DAB . Vậy số đo DCB
ˆ
là:
A. 600 B.1200 C.900 D.Một kết quả khác
Câu 5: Diện tích của hình quạt tròn cung 1200 của đường tròn bán kính 3cm là:
A .
(cm2 ) B . 2
(cm2 ) C . 3
(cm2 ) D . 4
(cm2 )
Câu 6: Độ dài của cung tròn 600 của một đường tròn có bán kính 4cm:
A. 5
cm B.
3
4
cm C.
19
3
cm D.
4
3
cm
II. Phần tự luận: (7 điểm)
Câu 7(1,5đ): Tính độ dài, diện tích hình quạt tròn có bán kính 8cm, số đo cung 400( làm tròn đến
chữ số thập phân thứ hai).
Câu 8(1,5 điểm):Cho hình vuông ABCD cạnh 6cm nội tiếp đường tròn (O). Tính diện tích phần
giới hạn bởi hình vuông và hình tròn.
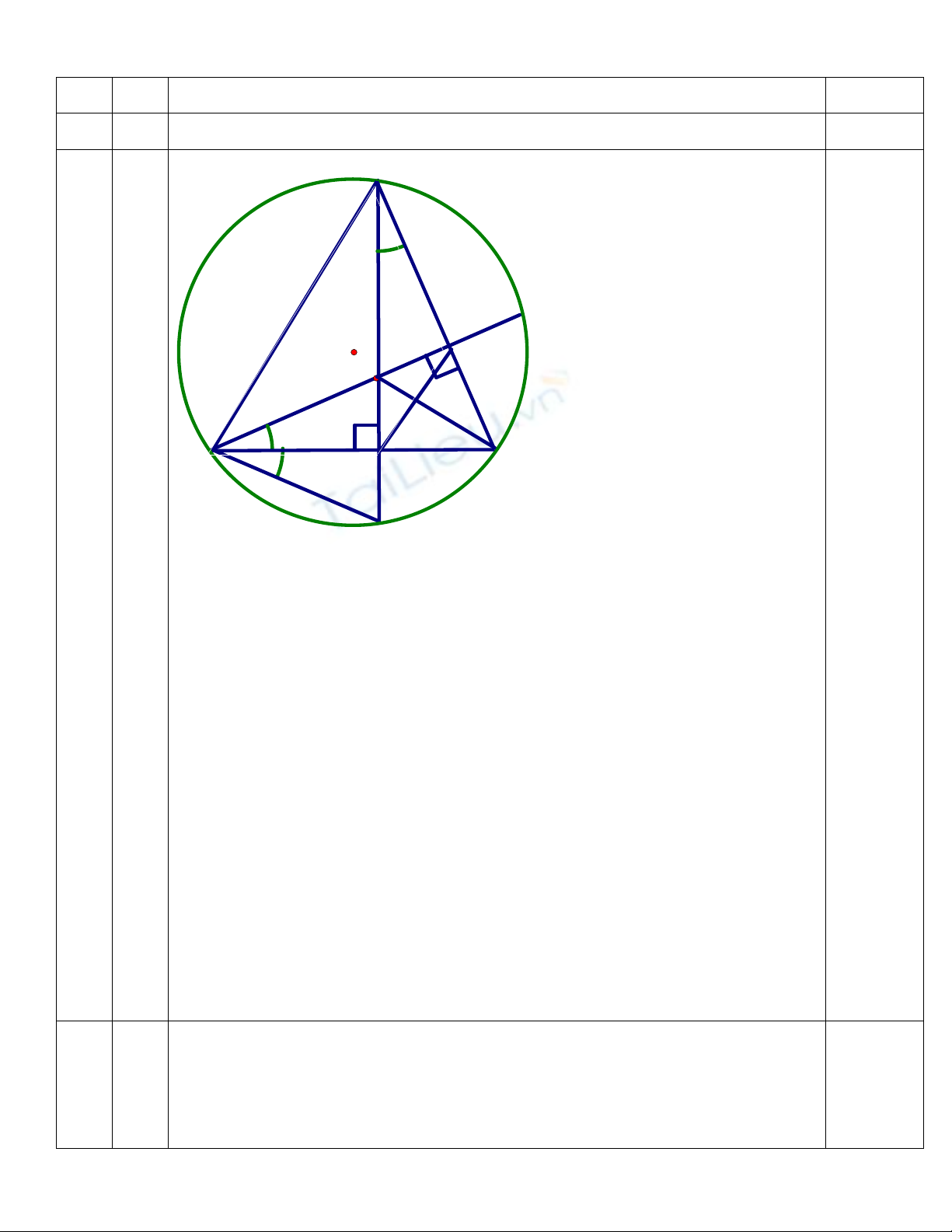
Câu 9(4đ): Cho tam giác ABC nhọn nội tiếp đường tròn (O),các đường cao AK và BI cắt nhau
tại H và cắt đường tròn (O) lần lượt tại D và E.
a)Chứng minh rằng tứ giác HICK,AIKB nội tiếp.
b)Chứng minh : CD = CE.
c) Chứng minh : CD = CH.
HẾT
ĐÁP ÁN VÀ THANG ĐIỂM
Câu Ý Nội dung Điểm
1 B 0,5đ
2 C 0,5đ
3 C 0,5đ
4 A 0,5đ
5 C 0,5đ
6 D 0,5đ
7 Độ dài cung tròn có bán kính 8cm,số đo cung 40
là:
0 0
0 0
. . 3,14.8.40
5,58
180 180
Rn
l
(cm)
Diện tích hình quạt tròn có bán kính 8cm,số đo cung 400 là:
. 8.5,58
2 2
q
Rl
S = 22,33 (cm2 )
0,75đ
0,75đ
8 HS vẽ hình đúng
Diện tích hình vuông là :
1
S
= 62 = 36 cm2
Bán kính đường tròn ngoại tiếp hình vuông: R = 6
2
2
= 3
2
cm
Diện tích hình tròn ngoại tiếp hình vuông :
2
2
.(3 2 )
S
= 18
cm2
Diện tích phần giới hạn bởi hình vuông và hình tròn:
S =
1
S
-
2
S
= 18
- 36 = 20,52 cm2
0,25đ
0,25đ
0,25đ
0,5đ
9
a
Xét tứ giác HICK có :
0 0 0
90 90 180
HIC HKC
nên tứ giác HICK nội tiếp
đường tròn đường kính HC.
Xét tứ giác AIKB có
0
90
AIB BKA
nên I,K cùng nhìn đoạn AB
cố định dưới một góc vuông.
Suy ra: I,K cùng nằm trên đường tròn đường kính AB.
Vậy tứ giác AIKB nội tiếp.
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
b Ta có :
0
1
 90
ACB
( hai góc phụ nhau )
0
1
90
B ACB
( hai góc phụ nhau )
H
D
E
1
1
2
B
C
O
A
K
I
Suy ra :
1
1
Â
B
Mà 1
1
Â
2
Sđ
DC
(
1
Â
góc nội tiếp chắn cung DC)
1
B
=
1
2
Sđ
EC
(
1
B
góc nội tiếp chắn cung EC)
Suy ra
DC
=
EC
DC = EC (liên hệ giữa cung và dây)
0,5đ
0,5đ
0,5đ
c
1
B
=
1
2
Sđ
EC
(
1
B
góc nội tiếp chắn cung EC)
2
B
=
1
2
Sđ
DC
(
2
B
góc nội tiếp chắn cung DC)
Mà
DC
=
EC
Suy ra :
1
B
=
2
B
Do đó
BHD
cân tại B(BK vừa là đường cao vừa là đường phân giác)
BC là đường trung trực của HD
Suy ra : CD = HC
0,25đ
0,25đ
0,25đ
0,25đ
Học sinh làm cách khác đúng vẫn cho điểm tối đa
Quảng Lợi,ngày 06 tháng 04 năm 2012
Giáo viên
Nguyễn Hữu Quang