Ti t 39ế
Tu n 32ầ
Ngày so n: 28/03/2014ạ
KI M TRA 45’.Ể
A. M C TIÊUỤ
1. Ki n th c:ế ứ
-N m đ c các đ nh nghĩa đ ng th ng vuông góc v i m t ph ng,ắ ượ ị ườ ẳ ớ ặ ẳ
đ ng th ng vuông góc v i đ ng th ng và góc gi a đ ng th ngườ ẳ ớ ườ ẳ ữ ườ ẳ
v i m t ph ng.ớ ặ ẳ
-N m đ c ph ng pháp ch ng minh đ ng th ng vuông góc v iắ ượ ươ ứ ườ ẳ ớ
m t ph ng, đ ng th ng vuông góc v i đ ng th ng.ặ ẳ ườ ẳ ớ ườ ẳ
2. K năng:ỹ
- Ch ng minh đ c đ ng th ng vuông góc v i m t ph ng, đ ngứ ượ ườ ẳ ớ ặ ẳ ườ
th ng vuông góc v i đ ng th ng.ẳ ớ ườ ẳ
- Xác đ nh đ c góc gi a đ ng th ng và m t ph ng.ị ượ ữ ườ ẳ ặ ẳ
3. Thái đ :ộ
- Nghiêm túc làm bài.
B. Biên so n đ ki m traạ ề ể
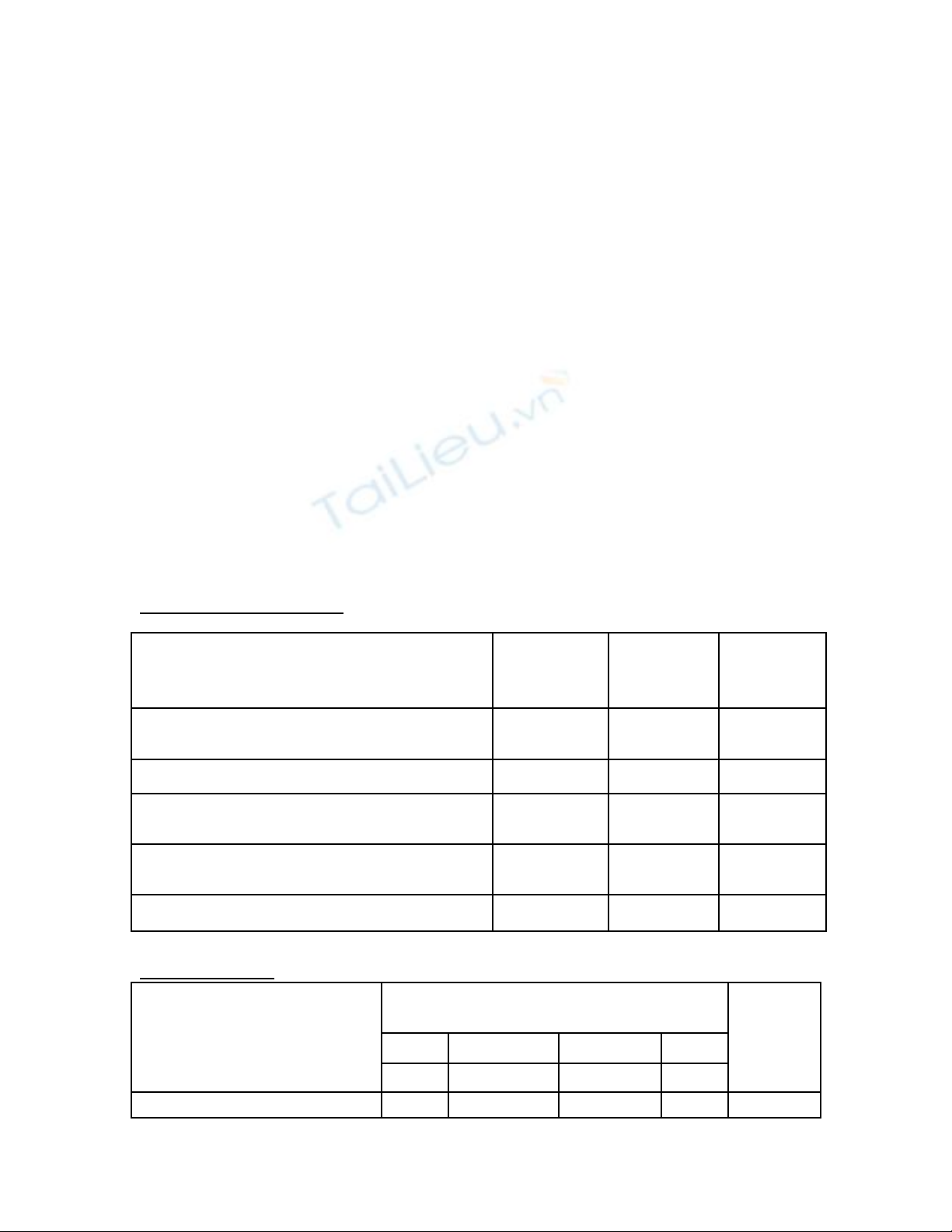
1.Ma tr n nh n th cậ ậ ứ
Ch đ ho c m ch ki n th c, kủ ề ặ ạ ế ứ ỹ
năng
T mầ
quan
tr ngọTr ng sọ ố T ngổ
đi mể
1.Ch ng minh m t đ ng th ngứ ộ ườ ẳ
vuông góc v i m t m t ph ng.ớ ộ ặ ẳ 25 2 50
2. Tính góc gi a hai đ ng th ng.ữ ườ ẳ 25 2 50
3. Ch ng minh hai đ ng th ngứ ườ ẳ
vuông góc. 25 2 50
4.Tính góc gi aữ đ ng th ng ườ ẳ và m tặ
ph ng.ẳ25 3 75
100% 225
2. Ma tr n đậ ề
Ch đ ho c m chủ ề ặ ạ
ki n th c, k năngế ứ ỹ
M c đ nh n th c – Hình th cứ ộ ậ ứ ứ
câu h iỏT ngổ
đi m/ể
10
1 2 3 4
TL TL TL TL
1.Ch ng minh m tứ ộ Câu 1a 1
đ ng th ng vuông gócườ ẳ
v i m t m t ph ng.ớ ộ ặ ẳ 1,0 2,5
2. Tính góc gi a haiữ
đ ng th ng.ườ ẳ Câu 1b
1,0
1
2,5
3. Ch ng minh haiứ
đ ng th ng vuông góc. ườ ẳ Câu 1c
1,0
1
2,5
4.Tính góc gi a đ ngữ ườ
th ng ẳvà m t ph ng.ặ ẳ Câu 1d
1,0
1
2,5
10,0
3.Di n gi i: ễ ả Đ BÀIỀ
a) (2.5 đi m)Ch ng minh m t đ ng th ng vuông góc v i m t m tể ứ ộ ườ ẳ ớ ộ ặ
ph ng.ẳ
b) (2.5 đi m) Tính góc gi a hai đ ng th ng.ể ữ ườ ẳ
c) (2.5 đi m)Ch ng minh hai đ ng th ng vuông góc. ể ứ ườ ẳ
d) (2.5 đi m)Tính góc gi a đ ng th ng ể ữ ườ ẳ và m t ph ng.ặ ẳ
Đ BÀIỀ
Cho hình chóp S.ABCD có SA vuông góc v i m t ph ng (ABCD) và đáyớ ặ ẳ
ABCD là m t hình vuông tâm O v i SA=AB=a.ộ ớ
Câu 1 (2,5 đi m).ể Ch ng minh BD vuông góc v i m t ph ng (SAC).ứ ớ ặ ẳ
Câu 2 (2,5 đi m).ể Tính góc gi a SC và ADữ
Câu 3 (2,5 đi m).ể G i H là hình chi u vuông góc c a O lên đ ng th ng SC.ọ ế ủ ườ ẳ
Xác đ nh và tính s đo c a góc gi a đ ng th ng BH và m t ph ng (SAC).ị ố ủ ữ ườ ẳ ặ ẳ
Câu 4 (2,5 đi m).ể G i E là trung đi m SB, ch ng minh AE vuông góc v i SC ọ ể ứ ớ
ĐÁP ÁN
N i dungộĐi mể
Câu 1 (2,5 đi m). ểS
DA
C
B
E
H
O
Hình v (ch a có BH, DH và OH)ẽ ư
Vì SA ⊥(ABCD) nên SA ⊥BD (1)
Vì ABCD là m t hình vuông nên AC ộ⊥BD (2)
SA và AC c t nhau trong mp(SAC) (3)ắ
T (1), (2),(3) ừ⇒ BD⊥(SAC)
0,5
0,5
0,5
0,5
0,5
Câu 2 (2,5 đi m). ể
- Ch ra tam giác SBC vuông t i Bỉ ạ
-Vì BC // AD nên góc gi a AD và SC b ng góc gi a BC và SC và b ngữ ằ ữ ằ
góc
·
SCB
- Ta có:
·
2
tan 2
SB a
SCB
BC a
= = =
1,0
0,5
1,0
Câu 3 (2,5 đi m). ể
Vì BD⊥(SAC) và OH⊂(SAC) nên BD⊥OH
⇒ Tam giác OBH vuông t i O và OH là hình chi u vuông góc c a BH lênạ ế ủ
mp(SAC) ⇒ góc nh n ọ
·
BHO
là góc gi a BH và mp(SAC)ữ
Vì SA⊥(ABCD) nên SA⊥AC⇒ Tam giác SAC vuông t i A có:ạ
SA=a và AC=
a 2
⇒
2 2
SC SA AC a 3= + =
OHC∆
đ ng d ng v i ồ ạ ớ
SAC∆
nên:
a 2
OH OC a 2
2
OH .a
SA SC a 3 2 3
= ⇒ = =
Tam giác OBH vuông t i O có: ạ
⇒
·
BHO
=600
V y góc gi a đ ng th ng BH và m t ph ng (SAC) là ậ ữ ườ ẳ ặ ẳ
·
BHO
=600
0,5
0,5
0,5
0,5
0,5
Câu 4 (2,5 đi m). ể
- Ch ra AE vuông góc v i SB (4)ỉ ớ
- Ch ra BC vuông góc v i AE (5)ỉ ớ
- BC và SB c t nhau trong mp(SBC) (6)ắ
T (4),(5),(6) suy ra AE vuông góc mp(SBC) ừ
Do đó AE vuông góc v i SCớ
0,5
0,5
0,5
0,5
0,5