Đề kiểm tra giữa học phần Vật lý 1

Chia sẻ: Minh Minh | Ngày: | Loại File: PDF | Số trang:4

Thêm vào BST

Báo xấu

128
lượt xem 14
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Đề Kiểm tra giữa học phần Vật lý 1 gồm 5 câu kèm đáp án giúp bạn làm quen với hình thức thi của môn học, hệ thống lại kiến thức qua các câu hỏi, bài tập và tự đánh giá năng lực của mình. Mời bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề kiểm tra giữa học phần Vật lý 1

Kiểm tra giữa học phần Vật lý 1 Thời gian làm bài : 60 phút (không tính thời gian chép đề) Bài 1: (2 điểm) Một người đứng ở độ cao H so với mặt đất, ném ngang một vật vào cửa sổ nhà đối diện cách chỗ ném s, mép trên cửa sổ cách mặt đất h < H. Tìm vận tốc ném để vật rơi vào nhà và cách xa cửa sổ nhất. Bài 2: (1,5 điểm) Một đồng hồ treo tường có kim giờ dài 5cm, kim phút dài 8cm, kim giây dài 9cm. So sánh vận tốc góc, vân tốc dài và gia tốc hướng tâm của các đầu kim, biết các đầu kim chuyển động tròn đều. Bài 3: (3 điểm) Một vật khối lượng m1 có thể trượt trên mặt phẳng nghiêng góc  so với phương ngang, được nối với vật m2 bằng sợi dây nhẹ không dãn vắt qua ròng rọc. a) Bỏ qua khối lượng ròng rọc, xác định điều kiện của hệ số ma sát để vật m2 đi xuống đều và đi xuống nhanh dần đều. b) Thay m1 bằng hình trụ đặc bán kính r, khối lượng m3 và ròng rọc là đĩa tròn khối lượng m. Cho hệ số ma sát là k’ để m2 đi xuống. Tìm gia tốc của 2 vật. c) Trong câu b, lúc đầu m2 cách mặt đất h. Tính thời gian từ lúc m2 chuyển động đến khi chạm đất và vận tốc m2 khi chạm đất. Sau khi m2 chạm đất thì m3 chuyển động như thế nào? Bài 4: (2,5 điểm) Một quả cầu thép khối lượng m1 treo bằng dây dài h thả rơi với vận tốc đầu v0 khi dây hợp với phương ngang góc . Khi đến vị trí dây treo thẳng đứng quả cầu va chạm đàn hồi với vật m2 đang đứng yên trên mặt phẳng ngang. Sau va chạm vật m2 chuyển động được quãng đường s thì dừng lại, trước khi dừng m2 chạm nhẹ làm quả cầu m3 rời khỏi A chuyển động không ma sát vào đường rãnh ABCDE (như hình vẽ) với hA = 2.hE = n.R. a) Tính vận tốc m1, m2 sau va chạm và độ cao mà m1 lên được, hệ số ma sát của mặt phẳng ngang. b) Định điều kiện n để m3 không rời khỏi rãnh tại C và tìm vật tốc của m3 tại C và E. Bài 5: Chọn làm một trong 2 câu sau đây: (1 điểm) a) Một đĩa tròn đồng chất tâm O bán kính R, bị khoét một lỗ tròn nhỏ bán kính r tâm O’ cách O một đoạn R/2. Xác định khối tâm của đĩa và momen quán tính của đĩa đối với trục quay vuông góc qua O. b) Một vật dao động tắt dần có phương trình: x = 25.2-0,3.t.cos4t (cm). Tìm biên độ dao động của vật sau khi bắt đầu dao động 10s và sau 10 chu kỳ dao động toàn phần.
Kiểm tra giữa học phần Vật lý 1 Bài 1: Chọn Hệ quy chiếu gắn với mặt đất, hệ trục tọa độ Oxy như hình vẽ, gốc tọa độ tại vị trí bắt 0,5   đầu ném, gốc thời gian lúc bắt đầu ném. Vận tốc ném vật là v0 (theo phương ngang) Trong quá trình chuyển động vật chỉ chịu tác dụng của trọng lực (bỏ qua ma sát) nên theo định    0,25 luật II Newton ta có : a  g  x  v0 .t ax  0  vx  v0   g x2 0,5    g 2y . 2 a y  g v y  gt  y  t   2 v0  2 Điều kiện để vật rơi vào nhà là x = s và H - h  y  H – h – chiều cao cửa sổ. 0,25 Để vật rơi vào nhà và cách xa cửa sổ nhất thì vật phải rơi vào nhà tại mép trên cửa sổ là : g s2 g x = s và y = H – h  H  h  . 2  v0  s. 2 v0 2.( H  h) 0,5 Bài 2: Trong 1 h : kim giờ quay 1/12 vòng  (h) = /6 (rad/h) 0,5 Trong 1 h : kim phút quay 1 vòng  (m) = 2 (rad/h) Trong 1 h : kim giây quay 60 vòng  (s) = 120 (rad/h)  (h) : (m) : (s) = 1 : 12 : 720 0,5 Ta có : v = .R  v(h) : v(m) : v(s) = (h).5 : (m).8 : (s).9 = 5 : 96 : 6480 = 1 : 19,2 : 1296 0,5 Và an = 2.R  anh ) : anm) : ans )  5 :1152 : 4665600  1: 230, 4 : 933120 ( ( ( Bài 3:       a) Áp dụng định luật II Newton cho vật m1: P  N1  T1  f ms  m1 a1 1     0,25 Áp dụng định luật II Newton cho vật m2: P  T1  m2 a2 1 Chọn chiều dương chuyển động như hình vẽ, chiếu PT lên (+) ta được các giá trị đại số sau : 0,25 (1)/(+) : T1 – P1.sin - fms = m1.a1 và (2)/(+) : P2 – T2 = m2.a2 Vì dây nhẹ, không dãn và bỏ qua khối lượng ròng rọc nên a1 = a2 = a và T1 = T2 = T 0,25 Ta có : N1 = P1.cos = m1.g.cos và fms = k.N = k.m1.g.cos m2  m1 sin   km1 cos  (1’) + (2’) : m2.g – m1.g.sin – k.m1.g.cos = m1.a + m2.a  a  g 0,25 m2  m1 m2  m1 sin  Để m2 đi xuống đều : a = 0  k  m1 cos  0,25 m  m1 sin  Để m2 đi xuống nhanh dần đều : a > 0  k 2 m1 cos 
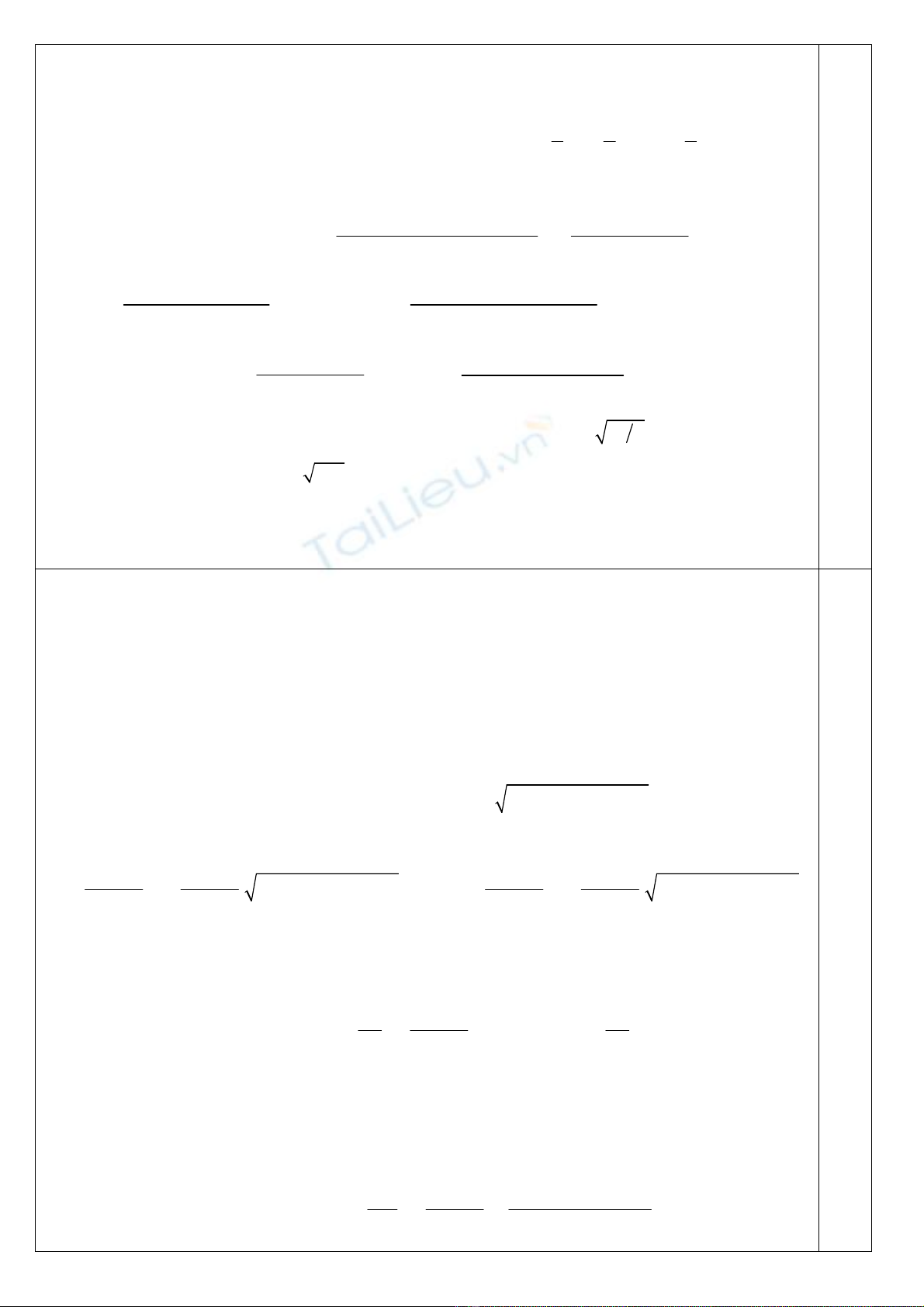
b) Tương tự câu a ta có phương trình chuyển động tịnh tiến của vật m2 và m3 : m2g – T2 = m2.a và T3 – m3.g.sin - fms = m3.a 0,25 1 a 1 0,25 Phương trình chuyển động quay quanh trục của m3 là : f ms .r  m3 r 2  f ms  m3a 2 r 2 Phương trình chuyển động quay quanh trục của ròng rọc là: T2 – T3 = ½.m.a 0,25 2m2  2m3 (k 'cos   sin  ) 2m2  2m3 sin  0,5 Từ các phương trình trên ta có: a  g g 2m2  2m3  m 2m2  3m3  m  3m  2m3 sin   m   3m2  2m2 sin   m sin   T2  m2 g  3  và T3  m3 g    2m2  3m3  m   2m2  3m3  m   m  m3 sin   m2  m3 sin  f ms  k '.m3 .g .cos   m3 .g .  2  và k '   2m2  3m3  m  (2m2  3m3  m) cos  c) Thời gian từ lúc m2 bắt đầu chuyển động đến khi chạm đất là: t  2h a 0,5 Vận tốc m2 lúc chạm đất là: v  2ah Sau khi m2 chạm đất vật m3 đi lên mặt phẳng nghiêng chậm dần đều một đoạn s3 rồi dừng lại và sau đó đi xuống nhanh dần đều. Bài 4: a) Chọn gốc thế năng tại điểm thấp nhất của bài toán. Độ cao ban đầu của vật m1 là : hA + h(1-cos). Trong quá trình chuyển động trước và sau khi va chạm, cơ năng của vật m1 được bảo toàn do 0,25 bỏ qua ma sát và lực tác dụng vào m1 là trọng lực (lực thế) và lực căng dây (không sinh công). Áp dụng định luật bảo toàn cơ năng cho m1 lúc ban đầu và trước khi va chạm với m2, ta có: mghA  mgh 1  cos    mv0 / 2  mghA  mv12 / 2  v1  2 gh 1  cos    v0 2 2 0,25 Khi m1 va chạm đàn hồi với m2, áp dụng các công thức trong va chạm đàn hồi, ta có: m1  m2 m  m2 2 2m1 2m1 2 v '1  .v1  1 . 2 gh 1  cos    v0 và v '2  .v1  . 2 gh 1  cos    v0 0,5 m1  m2 m1  m2 m1  m2 m1  m2 Áp dụng định luật bảo toàn cơ năng cho m1 từ sau khi va chạm với m2 đến lúc ở vị trí cao nhất, ta có: 2 '2 v '2  m  m2   v2  mghA  mv / 2  mghA  mgh '  h '  1   1 1  .  h 1  cos    0  0,25 2 g  m1  m2   2g  Khi m2 chuyển động trên mặt phẳng ngang thì thế năng không đổi, động năng giảm do lực ma sát sinh công cản. Áp dụng định lý động năng cho m2 từ lúc bắt đầu chuyển động sau va chạm đến khi dừng lại chạm vào m3, ta tính được hệ số ma sát của mặt phẳng ngang: 2 2 '2 v '2  2m1  2 gh 1  cos    v0 Ams  Fms .s  k .m2 .g .s  m v / 2  k  2   2 2  . 0,25 2 gs  m1  m2  2 gs
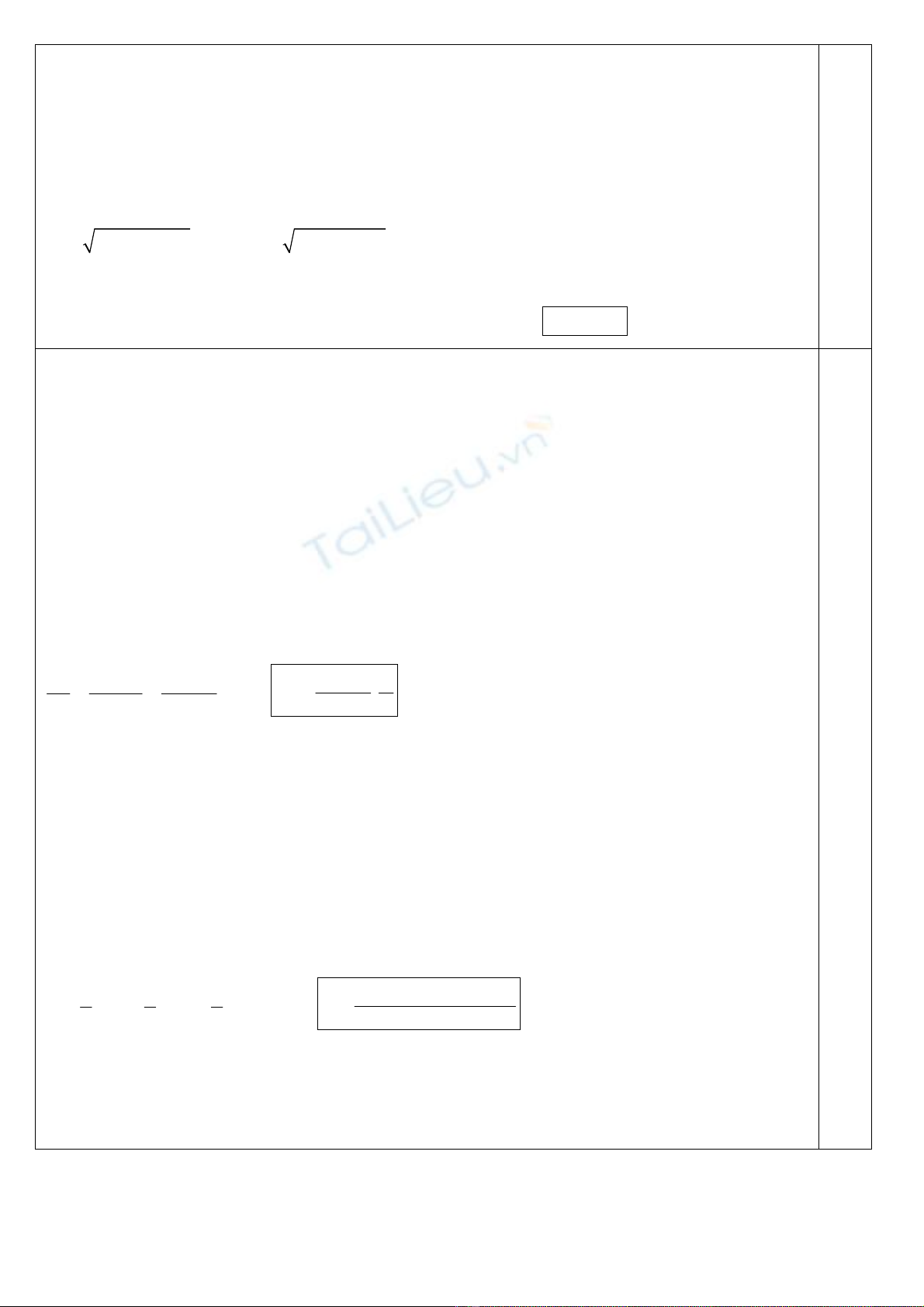
b) Quả cầu m3 chuyển động không ma sát, không vận tốc đầu trong đường rãnh ABCDE nên cơ năng của m3 bảo toàn trong suốt quá trình chuyển động do lực tác dụng vào m3 là trọng lực 0,25 (lực thế) và phản lực vuông góc của rãnh (không sinh công). Áp dụng định luật bảo toàn cơ năng cho m3 tại A, C, E ta có: 2 2 m3 ghA  m3 g .2 R  m3vC / 2  m3 ghE  m3vE / 2 vC  2.g (hA  2 R) và vE  2.g (hA  hE ) 0,25 Điều kiện để m3 không rời khỏi rãnh tại C là: NC  0. Áp dụng định luật II Newton ta có: 0,5 2 N c  m3 aC  m3 g  0  aC  vC / R  g  2 g (hA  2 R )  gR  hA  5R / 2 Bài 5: Chon 1 trong 2 cau a1) Xác định khối tâm của đĩa: Vì đĩa tròn đồng chất nên khối tâm của đĩa khi chưa bị khoét đặt tại O, khối tâm của phần đĩa còn lại (đã bị khoét) đặt tại C cách O một đoạn x. Do phần khoét là lỗ tròn nên khối tâm của phần đó đặt tại tâm O’ cách O một đoạn R/2. Ta thấy : đĩa chưa khoét = phần còn lại + phần khoét. Gọi khối lượng của các phần lần lượt là m, mc, mk, ta có : m = mc + mk. Chọn gốc tọa độ để xác định các khối tâm tại O, theo công thức tính khối tâm ta có: 0,25 m.rO = mc.rC + mk.rO’  x : R/2 = - mk : mc (vì rO = 0). Mà khối lượng đĩa tròn và phần lỗ tròn bị khoét tỷ lệ với bình phương bán kính nên ta có: mk mk r2 r2 R 0,25   2 2  x 2 2 . (dấu – cho biết C và O’ nằm ở 2 phía khác nhau mc m  mk R  r R r 2 so với O) a2) Xác định momen quán tính: Gọi I, Ic, Ik lần lượt là mômen quán tính của đĩa khi chưa bị khoét, phần đĩa còn lại đã bị khoét, phần đĩa bị khoét đối với trục quay qua tâm O và Ik’ là mômen quán tính của phần đĩa 0,25 bị khoét đối với trục quay qua tâm O’. Ta có: I = ½ m.R2 , Ik’ = ½ mk.r2. Theo định lý Huyghen – Stêne thì : Ik = ½ mk.r2 + mk.R2/4. Theo công thức tính momen quán tính ta có : Ic = I – Ik 0,25 1 1 1 m.(2 R 4  2r 4  R 2 .r 2 ) I c  mR 2  mk r 2  mk R 2  Ic  2 2 4 4R2 b) Từ PTdđ ta xác định được chu kỳ T = ½ s. Biên độ dao động của vật sau khi bắt đầu dao động 10s là: A = 25.2-3 = 22 = 4 (cm) 0,5 Biên độ dao động của vật sau 10 chu kỳ dao động toàn phần là : A = 25.2-3/2 = 27/2 = 11,3 (cm) 0,5