SỞ GD VÀ ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KIỂM TRA GIỮA KỲ I, NĂM HỌC 2020 - 2021
Môn: Toán 11
Thời gian làm bài: 90 phút (không tính thời gian giao đề)
- Họ và tên thí sinh: ..................................................................….– Số báo danh : ........................
Câu 1: Tìm tập xác định của hàm số
cos
sin 1
x
y
x
.
Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 5
y x
.
Câu 3: Tìm tập xác định của hàm số
y x
.
Câu 4: Tìm tập giá trị của hàm số
cos 2
y x
.
Câu 5: Cho các hàm số
cos
y x
,
sin
y x
,
tan
y x
,
cot
y x
. Trong các hàm số trên, có bao
nhiêu hàm số chẵn?
Câu 5: Giải phương trình
2cos 1 0
x
.
Câu 7: Giải phương trình
3 tan 2 3 0
x
.
Câu 8: Biểu diễn họ nghiệm của phương trình
sin 2 1
x
trên đường tròn đơn vị ta được bao nhiêu
điểm?
Câu 9: Giải phương trình 2
sin 2sin 0
x x
.
Câu 10: Giải phương trình
sin 3 cos 1
x x
.
Câu 11: Tìm m để phương trình
2
cos 1 cos 2 cos sin
x x m x m x
có đúng 2 nghiệm
2
;
3
0
x.
Câu 12: An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có bốn
con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách
chọn đường đi đến nhà Cường?
Câu 13: Cho các số
1,5, 6,7
có thể lập được bao nhiêu số tự nhiên có
4
chữ số với các chữ số khác
nhau.
Câu 14: Gọi
S
là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ
số
5,6,7,8,9.
Tính tổng tất cả các số thuộc tâp
.
S
Câu 15. Cho hình bình hành
ABCD
. Tìm ảnh của điểm
D
qua phép tịnh tiến theo véctơ
AB
.
Câu 16: Trong mặt phẳng tọa độ
Oxy
, cho vectơ
1;2
v
. Tìm ảnh của điểm
2;3
A qua phép tịnh
tiến theo vectơ
v
.
Câu 17: Trong mặt phẳng
Oxy
, cho vectơ
(3;3)
v
và đường tròn 2 2
( ) : 2 4 4 0
C x y x y
.
Ảnh của
( )
C
qua phép tịnh tiến vectơ
v
là đường tròn
( ')
C
. Viết phương trình
( ')
C
.
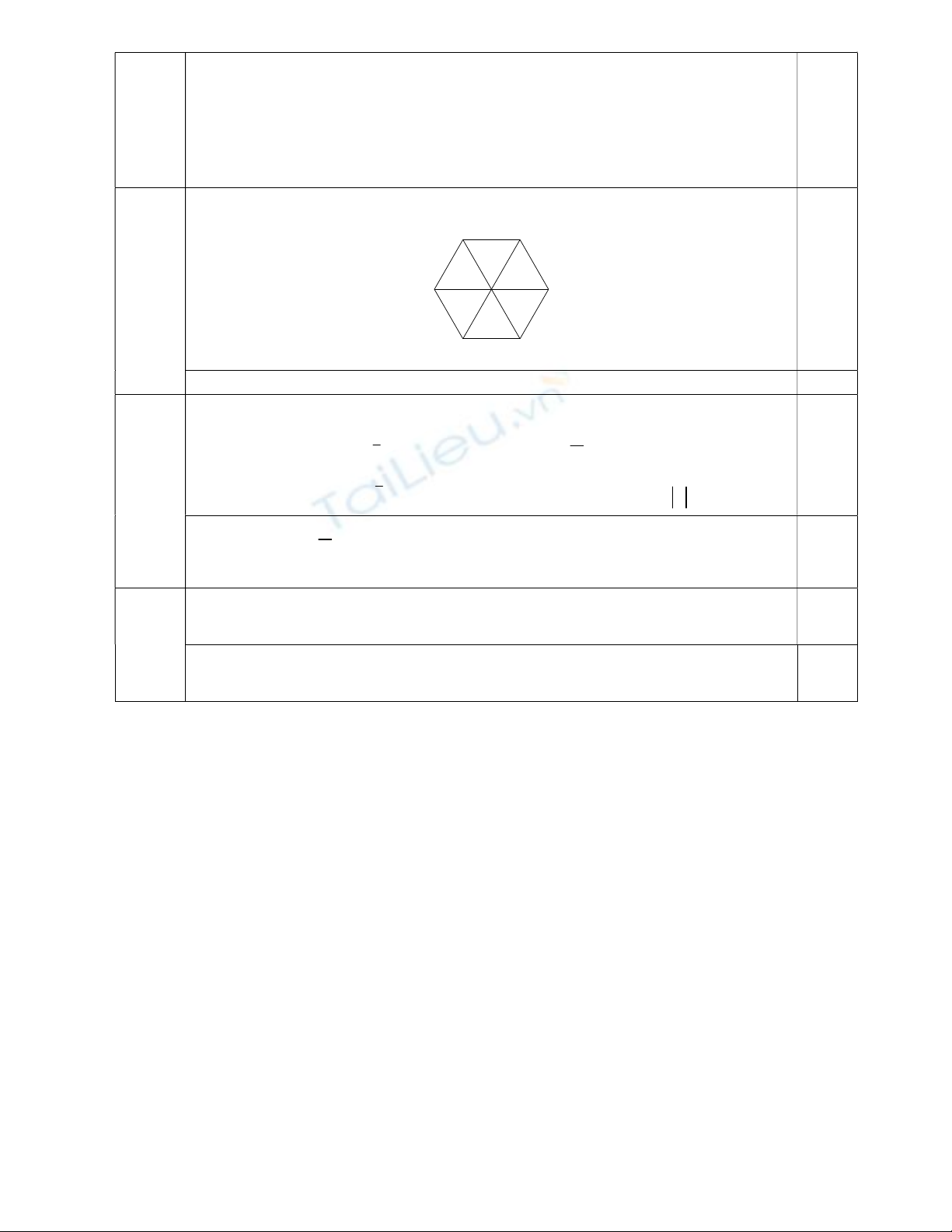
Câu 18: Cho lục giác đều
ABCDEF
tâm
O
như hình bên. Tìm ảnh của tam giác
AOF
qua phép quay
tâm
O
góc quay
0
120
.
O
F
ED
C
B
A
Câu 19: Trong mặt phẳng tọa độ
Oxy
cho điểm
3;0
A. Tìm tọa độ điểm
A
là ảnh của điểm
A
qua
phép quay tâm
0; 0
O góc quay
2
.
Câu 20: Trong mặt phẳng tọa độ
Oxy
, cho điểm
3; 1
A
. Tìm tọa độ điểm
B
sao cho điểm
A
là
ảnh của điểm
B
qua phép tịnh tiến theo véctơ
2; 1
u
.
_______ Hết _______
Cán bộ coi thi không giải thích gì thêm
HƯỚNG DẪN GIẢI
Câu Nội dung Điểm
1 Điều kiện
sin 1 s n0 1
2
i 2x x x k k
. 0.25
Vậy tập xác định 2| k\2D k
. 0.25
2 Ta có
1 sin 1
x
8 3sin 5 2
x
8 2
y
. 0.25
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là
2; 8
. 0.25
3 Hàm số
tan 2
y x
xác định khi
cos 2 0
x
2
2
x k
,
4 2
x k k
. 0.25
Vậy tập xác định của hàm số là \ ,
4 2
D k k
0.25
4 Ta có
1 cos 2 1
x
,x
. 0.25
Vậy tập giá trị của hàm số đã cho là
1;1
. 0.25
5 Hàm số chẵn là:
cos
y x
. 0.25
Vậy có 1 hàm số chẵn (HS có thể không cần lí giải các hàm số còn lại là lẻ) 0.25
6 Phương trình
2cos 1 0
x
1
cos
2
x
0.25
2
3
x k
. 0.25
7
3 tan 2 3 0 tan 2 3
x x 0.25
2
3
x k
6 2
x k k
. 0.25
8 Ta có:
sin 2 1 2 2
2
x x k
4
x k k
0.25
Biểu diễn họ nghiệm của
sin 2 1
x
trên đường tròn đơn vị ta được
2
điểm. 0.25
9 Ta có 2
sin 0
sin 2sin 0 .
sin 2
x
x x x
Vì
1 sin 1
x
nên chỉ có
sin 0
x
thỏa mãn.
0.25
Ta có
sin 0 ,
x x k
.
k
0.25
10
sin 3 cos 1
x x
1
sin
3 2
x
0.25
2
6
2
2
x k
x k
, k
0.25
11 Ta có
2
cos 1 cos2 cos sin
x x m x m x
cos 1 cos 2 cos 1 cos 1 cos
x x m x m x x
cos 1 cos 1
cos2 cos cos cos 2
x x
x m x m m x x m
0.25
Với
cos 1 2
x x k
: không có nghiệm 2
;
3
0
x.
Với 2
1
cos 2 cos
2
m
x m x
.
Trên
2
0;
3
, phương trình
cos
x a
có duy nhất 1 nghiệm với 1
;1
2
a
Do đó, YCBT
111
1 1 1
1 1
1
1 1
2 2 2
2
2 2
1 1 1
2 2
mmm
mm
mm
m
.
12 Từ nhà An đến nhà Bình có bốn cách chọn đường.
Từ nhà Bình đến nhà Cường có sáu cách chọn đường. 0.25
Áp dụng quy tắc nhân ta có số cách chọn đường đi từ nhà An đến nhà Cường là:
4.6 24
(cách). 0.25
13 Gọi số tự nhiên có
4
chữ số cần tìm là:
, 0
abcd a , khi đó:
a
có
4
cách chọn;
b
có
3
cách chọn;
c
có
2
cách chọn;
d
có
1
cách chọn 0.25
Vậy có:
4.3.2.1 24
số 0.25
14 Số các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ
5,6,7,8,9
là
5! 120
.
Vì vai trò các chữ số như nhau nên mỗi chữ số
5,6,7,8,9
xuất hiện ở hàng đơn vị là
4! 24
lần.
Tổng các chữ số ở hàng đơn vị là
24 5 6 7 8 9 840
.
0.25
Tương tự thì mỗi lần xuất hiện ở các hàng chục, trăm, nghìn, chục nghìn của mỗi
chữ số là 24 lần.
Vậy tổng các số thuộc tập
S
là
2 3 4
840 1 10 10 10 10 9333240
.
0.25
15
Ta có
AB DC
0.25
Nên phép tịnh tiến theo véctơ
AB
biến điểm
D
thành điểm
C
. 0.25
16 Ta có
v
T A A AA v
2 1
3 2
x
y
0.25
1
5
x
y
1;5
A. 0.25
17 Ta có 2 2
( ) : 2 4 4 0
C x y x y
2 2
1 2 9
x y
.
Vậy đường tròn
C
có tâm
1; 2
I
và bán kính
3
R
. 0.25
A
B
C
D
Gọi
;v
I x y T I
khi đó ta có
1 3
2 3
x
y
4
1
x
y
.
Do phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính nên phương
trình đường tròn
C
là: 2 2
( ) : ( 4) ( 1) 9
C x y
.
0.25
18
O
F
ED
C
B
A
0.25
Trả lời được ảnh là tam giác EOD 0.25
19
Gọi
;
A x y
. Ta có
,2,
2
O
OA OA
Q A A OA OA
.
Vì
,2
3; 0 0;
OA OA
A Ox A Oy A y

. Mà
3
OA OA y
.
0.25
Do góc quay
0
2
y
. Vậy
0; 3
A.
Chấp nhận học sinh chỉ vẽ hình và nêu được kết quả.
0.25
20 Ta có
u
T B A
BA u
3 2
1 1
x
y
0.25
1
0
x
y
1;0
B. 0.25