ĐỀ KIỂM TRA HỌC KÌ II MÔN TOÁN
LỚP 7
Họ và tên:……………………………….................……
Lớp:………………… SBD:……………………….……. Thời gian làm bài: 90 phút (Không kể thời
gian giao đề)
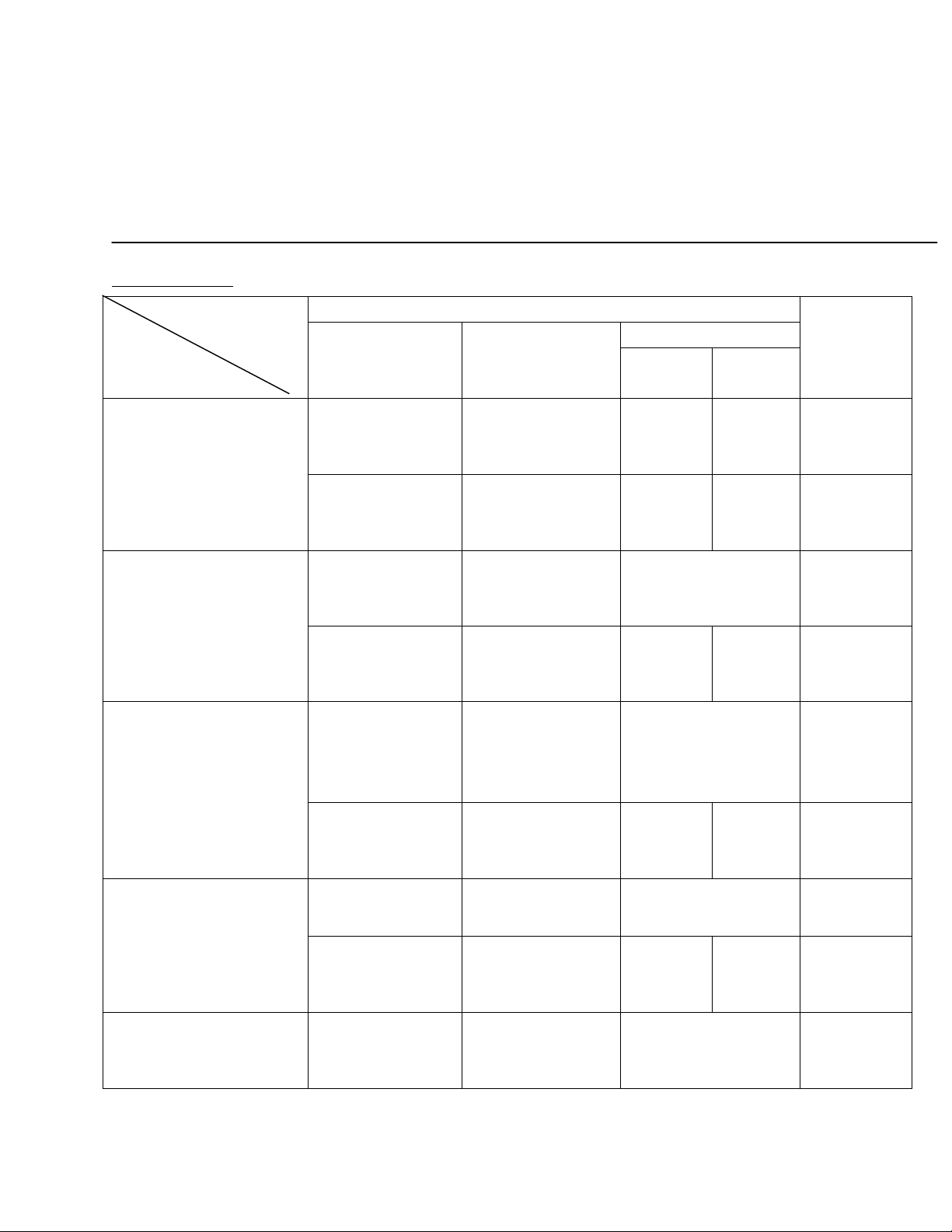
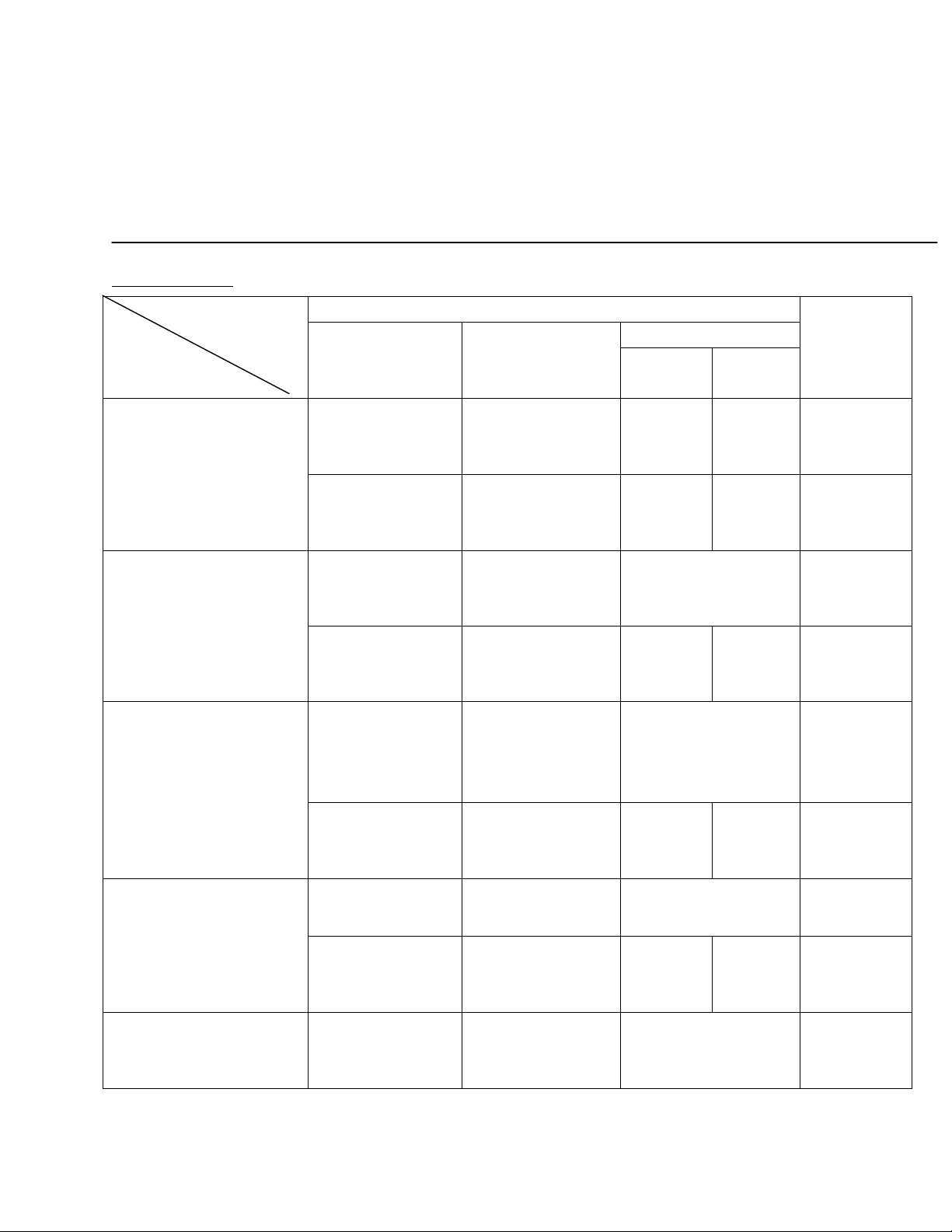
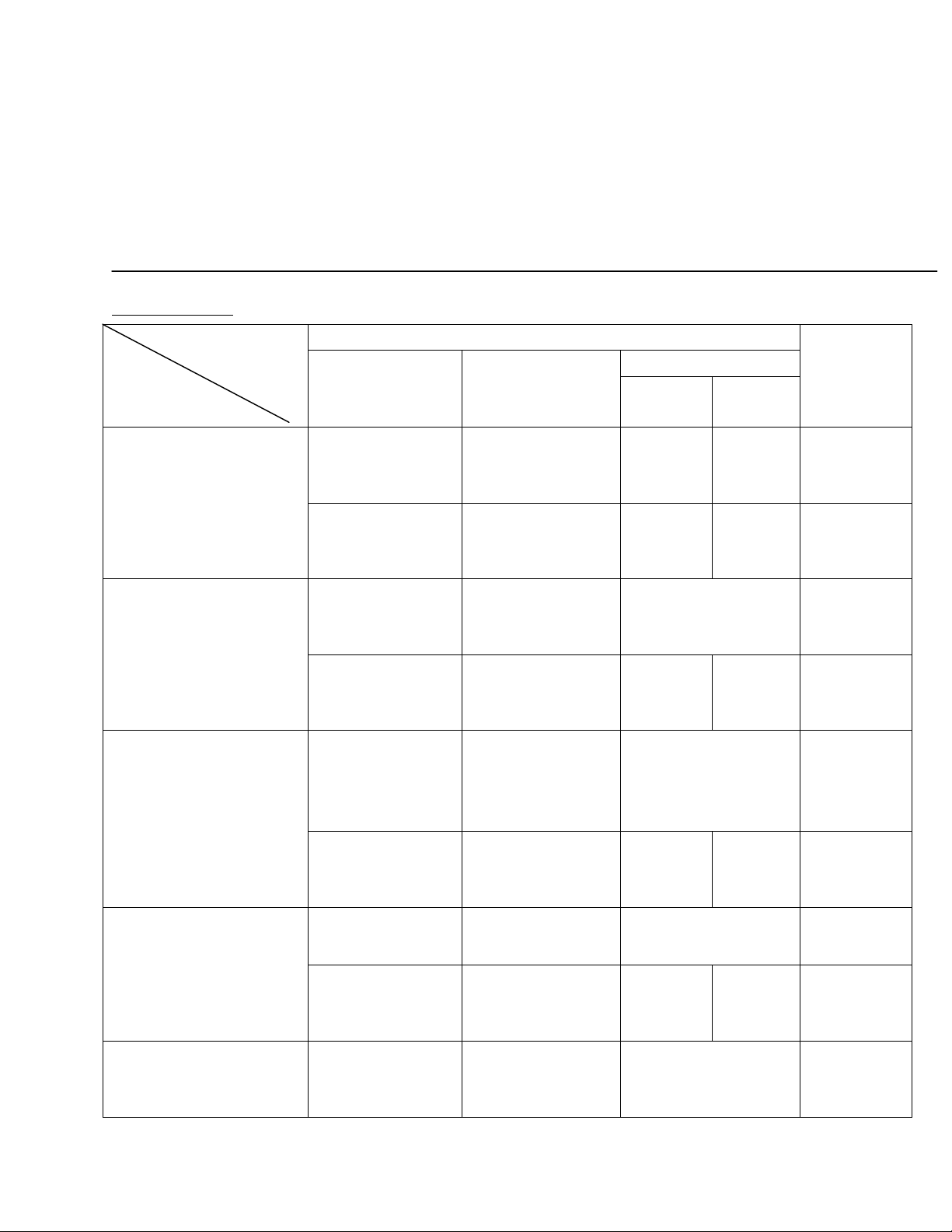
A.MA TRÂN
Cấp độ
Chủ đề
Mức độ kiến thức
Tổng
Nhận biết
Thông hiểu
Vận dụng
Cấp độ
thấp
Cấp độ
cao
Đơn thức
Số câu:
Số điểm:
Tỉ lệ %:
Nhân hai đơn
thức
Tính:
0,5
0,5
1
1,0
Tỉ lệ:10%
Thống kê
Số câu:
Số điểm:
Tỉ lệ %:
Nhận biết dấu
hiệu
Lập bảng tần số
Tính số trung bình
cộng
0,5
1,0
1,0
1
2,5
Tỉ lệ 25%
Đa thức
Số câu:
Số điểm:
Tỉ lệ %:
Sắp xếp các
hạng tử theo
lũy thừa của
biến
Cộng,trừ da thức
0,5
2,0
1
2,5
Tỉ lệ 25%
Các đường đồng
qui trong tam giác
Số câu:
Số điểm:
Tỉ lệ %:
T/chất đường
trung tuyến
Vẽ hình, viết gt-
kl
Chứng minh...
0,5
0,5
2,5
0,5
2
4.0
T
ỉ lệ 40%
T
ổng
Số câu:
Số điểm:
Tỉ lệ %:
1,0
T
ỉ lệ 10%
2,5
T
ỉ lệ 25%
6,5
T
ỉ lệ 65%
5
10,0
T
ỉlệ 100%