
S GD & ĐT Đ NG THÁP Ở Ồ
TR NG THPT TÂN THÀNHƯỜ
Đ KI M TRA H C KỲ 2 – TOÁN 10 Ề Ể Ọ (tham kh o)ả
Th i gian: 90 phútờ
Năm h c: 2012 – 2013 ọ
I. PH N CHUNG CHO T T C CÁC H C SINH (Ầ Ấ Ả Ọ 8,0 đi mể)
Câu I (3,0 đi m)ể
1) Xét d u bi u th c: ấ ể ứ
( )
2
2 6f x x x= − −
2) Gi i các b t ph ng trình sau: ả ấ ươ
a)
2
2 3 5 0x x+ − >
b)
2
2 5 1
6 7 3
x
x x x
−<
− − −
Câu II (3,0 đi m)ể
1) Cho
2
sin 3
α
=
,
2
πα π
< <
. Tính
cos , tan , cot
α α α
2) Ch ng minh r ng :ứ ằ
−=
−
2 2 6
2 2
sin tan tan
cos cot
x x x
x x
(v i ớx là giá tr đ bi u th c có nghĩa)ị ể ể ứ
Câu III (2,0 đi m)ể
Trong m t ph ng v i h t a đ Oxy, cho A(1;5) và đ ng th ng (d): ặ ẳ ớ ệ ọ ộ ườ ẳ
4 3 1 0.x y− + =
1) Vi t ph ng trình t ng quát c a đ ng th ng (a) đi qua đi m A và vuông góc v i đ ngế ươ ổ ủ ườ ẳ ể ớ ườ
th ng (d).ẳ
2) Vi t ph ng trình đ ng tròn (C) có tâm A và ti p xúc v i đ ng th ng (d).ế ươ ườ ế ớ ườ ẳ
II. PH N RIÊNG – PH N T CH N (Ầ Ầ Ự Ọ 2,0 đi mể)
A. PH N 1 (THEO CH NG TRÌNH CHU N)Ầ ƯƠ Ẩ
Câu IVa ( 2,0 đi m)ể
1) Cho ph ng trình: ươ
− + − + =
2 2
6 2 2 9 0x mx m m
. Tìm các giá tr c a ị ủ m đ ph ng trình có haiể ươ
nghi m d ng phân bi t.ệ ươ ệ
2) Trong m t ph ng v i h to đ Oặ ẳ ớ ệ ạ ộ xy, vi t ph ng trình đ ng tròn đ ng kính AB bi tế ươ ườ ườ ế
( 1;1)A−
, B(5; 3)
B. PH N 2 (THEO CH NG TRÌNH NÂNG CAO)Ầ ƯƠ
Câu IVb (2,0 đi m)ể
1) Tìm m đ b t ph ng trình: ể ấ ươ
( )
2
( 1) 2 1 3 3 0m x m x m+ − − + − ≥
có nghi m đúng v i m i giá trệ ớ ọ ị
c a ủx.
2) L p ph ng trình chính t c c a hypebol (H) bi t (H) đi qua N(6;3) và góc gi a hai ti m c nậ ươ ắ ủ ế ữ ệ ậ
b ng ằ
0
60
-------------------------H t--------------------------ế
1

ĐÁP ÁN
Đáp án Điể
m
Câu I 1Xét d u bi u th c: ấ ể ứ
( )
2
2 6f x x x= − −
Ph ng trình ươ
2
2 6 0x x− − =
có hai nghi m x = 2 và ệ
3
2
x= −
0.25
BXD
x
−∞
3
2
−
2
+∞
f(x) + 0 - 0 +
0.5
KL:
( )
3
( ) 0 ; 2;
2
f x x −
> ∀ ∈ −∞ ∪ +∞
÷
3
( ) 0 ;2
2
f x x
< ∀ ∈ −
÷
0.25
2Gi i các b t ph ng trình sauả ấ ươ :
a)
2
2 3 5 0x x+ − >
Đ t ặ
2
( ) 2 3 5f x x x= + −
Ph ng trình ươ
2
2 3 5 0x x+ − =
có hai nghi m x = 1 và ệ
5
2
x= −
0.25
BXD
x
−∞
5
2
−
1
+∞
f(x) + 0 - 0 +
0.5
T p nghi m c a b t ph ng trình là ậ ệ ủ ấ ươ
( )
5
; 1;
2
T
= −∞ − ∪ +∞
÷
0.25
b.
2
2 5 1
6 7 3
x
x x x
−<
− − −
( )
( )
2 2
2
2
2 5 1 2 5 1
0
6 7 3 6 7 3
5 22 0
3 6 7
x x
x x x x x x
x x
x x x
− −
< ⇔ − <
− − − − − −
− +
⇔ <
− − −
0.25
BXD
x
−∞
-1 3 7
+∞
2
5 22x x− +
+ + + +
x-3 - - 0 + +
2
6 7x x− −
+ 0 - - 0 +
VT - + - +
0.5
V y b t ph ng trình có t p nghi m là: ậ ấ ươ ậ ệ
( ) ( )
; 1 3;7T= −∞ − ∪
0.25
Câu II 1Cho
2
sin 3
α
=
,
2
πα π
< <
. Tính
cos , tan , cot
α α α
Ta có:
2
2 2
2 5
cos 1 sin 1 3 9
α α
= − = − =
÷
5
cos 3
α
⇒ = ±
0.5
0.5
2

Do
2
πα π
< <
nên
5
cos 0 cos 3
α α
< ⇒ = −
2
sin 2
3
tan cos 5 5
3
α
αα
= = = −
−
0.25
5
cot 2
α
= −
0.25
2Ch ng minh r ng :ứ ằ
−=
−
2 2 6
2 2
sin tan tan
cos cot
x x x
x x
(v i x là giá tr đ bi u th cớ ị ể ể ứ
có nghĩa)
2
2 2 2
2 2
2
2
2
24 2
2
24 2
2
2
6
1
sin 1
sin tan cos
1
cos cot cos 1 sin
cos 1
sin . sin ( sin )
cos
= sin 1 cos ( cos )
cos . sin
=tan
= VP (dpcm)
x
x x x
VT x x xx
x
xx x
x
xx x
xx
x
−
÷
−
= =
−
−
÷
−−
=
−−
0.5
0.5
0.5
Câu
III
Trong m t ph ng v i h t a đ Oxy, cho A(1;5) và đ ng th ng (d):ặ ẳ ớ ệ ọ ộ ườ ẳ
4 3 1 0.x y− + =
1Vi t ph ng trình t ng quát c a đ ng th ng (d’) đi qua đi m A vàế ươ ổ ủ ườ ẳ ể
vuông góc v i đ ng th ng (d).ớ ườ ẳ
Do d’ vuông góc v i d nên d’ có ph ng trình: 3x + 4y + c = 0ớ ươ 0.5
Vì d’ đi qua A(1; 5) nên ta có: 3.1 + 4.5 + c = 0
23c
⇒ = −
0.25
Do đó d’ có ph ng trình t ng quát là: 3x + 4y - 23 = 0ươ ổ 0.25
2Vi t ph ng trình đ ng tròn (C) có tâm A và ti p xúc v i đ ngế ươ ườ ế ớ ườ
th ng (d).ẳ
Bán kính c a đ ng tròn (C):ủ ườ
( )
2
2
4.1 3.5 1
( , ) 2
4 3
R d A d − +
= = =
+ −
0.5
Ph ng trình đ ng tròn:ươ ườ
( ) ( )
2 2
1 5 4x y− + − =
0.5
Câu
Iva
1Cho ph ng trình: ươ
− + − + =
2 2
6 2 2 9 0x mx m m
. Tìm các giá tr c a m đị ủ ể
ph ng trình có hai nghi m d ng phân bi t.ươ ệ ươ ệ
Đ ph ng trình có 2 nghi m d ng phân bi t khi và ch khi:ể ươ ệ ươ ệ ỉ
0.25
3

' 0
0
0
b
a
c
a
∆ >
− >
>
2 2
2 2
9 (2 2 9 ) 0 2 2 0
6 0 0
9 2 2 0 9 2 2 0
11
m m m m
m m
m m m m
mm
m
− − + > − >
⇔ > ⇔ >
− + > − + >
>
⇔ ⇔ >
∀
0.5
0.25
V y v i m > 1 thì ph ng trình có 2 nghi m d ng phân bi t.ậ ớ ươ ệ ươ ệ
2Trong m t ph ng v i h to đ Oxy, vi t ph ng trình đ ng trònặ ẳ ớ ệ ạ ộ ế ươ ườ
đ ng kính AB bi t ườ ế
( 1;1)A−
, B(5; 3)
G i I(x; y) là trung đi m ABọ ể
1 5 2
2(2; 2)
1 3 2
2
x
I
y
− +
= =
⇒
+
= =
V y đ ng tròn có tâm I(2; 2)ậ ườ
0.25
Ta có
( ) ( )
2 2
( 3; 1) 3 1 10IA IA= − − ⇒ = − + − =
uur
0.25
V y ậ
10R IA= =
0.25
Ph ng trình c a đ ng tròn đ ng kính AB làươ ủ ườ ườ
( ) ( )
2 2
2 2 10x y− + − =
0.25
Câu
IVb
1Tìm m đ b t ph ng trình: ể ấ ươ
( )
2
( 1) 2 1 3 3 0m x m x m+ − − + − ≥
có nghi mệ
đúng v i m i giá tr c a x.ớ ọ ị ủ
Đ b t ph ng trình nghi m đúng v i m i giá tr c a x thìể ấ ươ ệ ớ ọ ị ủ
[ ]
2
1
1 0
' 0 ( 1) ( 1).(3 3) 0
m
m
m m m
> −
+ >
⇔
∆ ≤ − − − + − ≤
0.5
2
11
2 v m 1
2 2 4 0
mm
m
m m
> − > −
⇔ ⇔
≤ − ≥
− − + ≤
0.25
1m
⇔ ≥
0.25
2L p ph ng trình chính t c c a hypebol (H) bi t (H) đi qua N(6;3) vàậ ươ ắ ủ ế
góc gi a hai ti m c n b ng ữ ệ ậ ằ
0
60
Ph ng trình các đ ng ti m c n là ươ ườ ệ ậ
b
y x
a
= ±
. Do góc gi a hai đ ngữ ườ
ti m c n là ệ ậ
0
60
và hai đ ng ti m c n đ i x ng nhau qua Ox, nên có haiườ ệ ậ ố ứ
tr ng h p:ườ ợ
- Góc gi a hai ti m c n và tr c hoành b ng ữ ệ ậ ụ ằ
0
30
, suy ra
0
1
tan 30 3
b
a= =
(1)
0.25
4
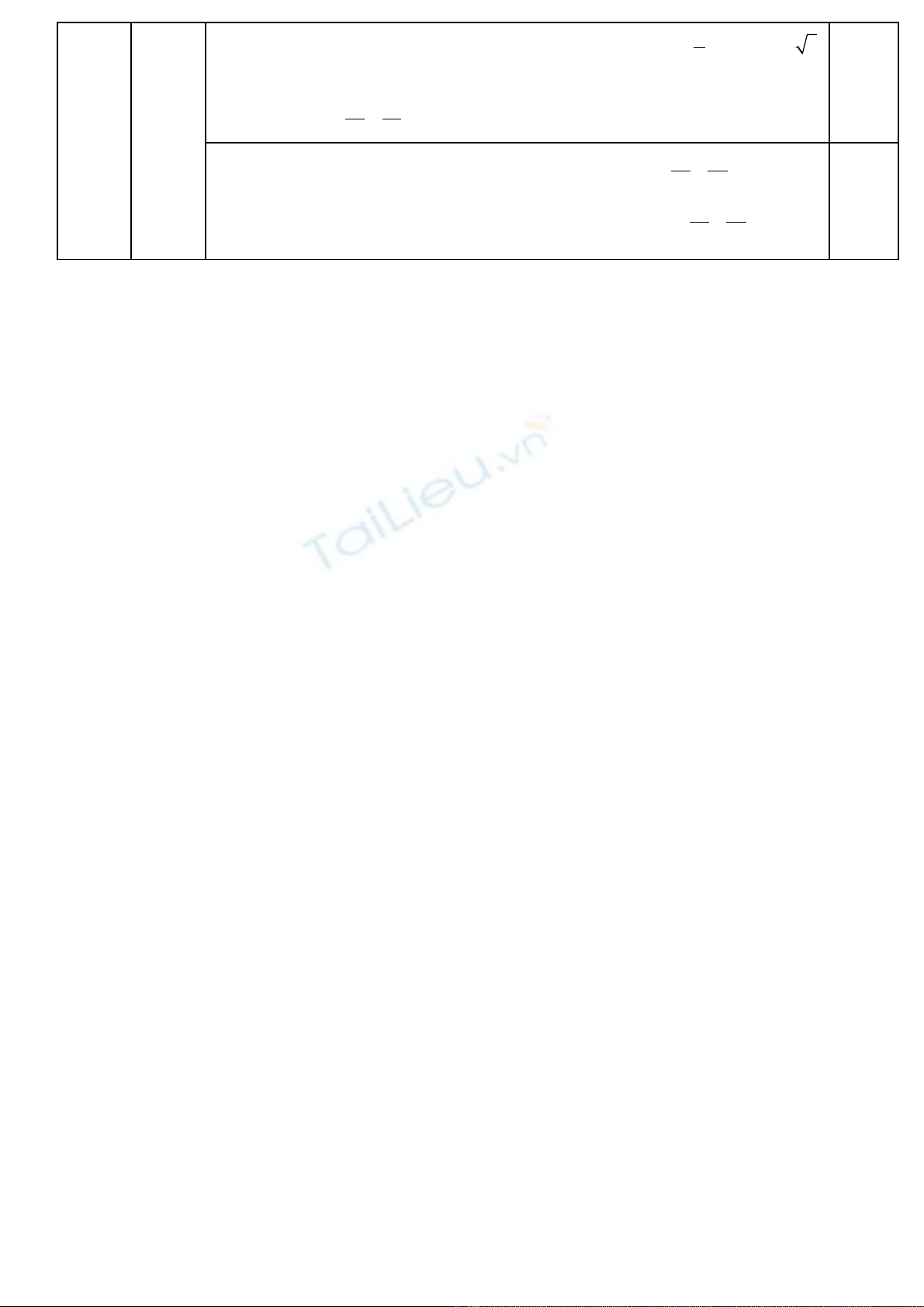
-Góc gi a m i ti m c n và tr c hoành b ng 60ữ ỗ ệ ậ ụ ằ 0, suy ra
0
tan 60 3
b
a= =
(2)
2 2
36 9
( ) 1N H a b
∈ ⇒ − =
(3)
0.25
T (1) và (3) suy ra ừ
2 2
9, 3a b= =
. Ta đ c hypebol (H): ượ
2 2
1
9 3
x y
− =
T (2) và (3) suy ra ừ
2 2
33, 99a b= =
. Ta đ c hypebol (H): ượ
2 2
1
33 99
x y
− =
0.25
0.25
H t.ế
5












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



