Đ KI M TRA GI A KÌ I L P 9Ề Ể Ữ Ớ
Năm h c: 2014 – 2015ọ
Môn: TOÁN
Th i gian làm bài 60 phútờ
Đ BÀIỀ
Câu 1 (1,5 đi m)ể
Th nào là hàm s b c nh t? ế ố ậ ấ
Áp d ng: V i giá tr nào c aụ ớ ị ủ m thì các hàm s sau là hàm s b c nh tố ố ậ ấ
a, y =
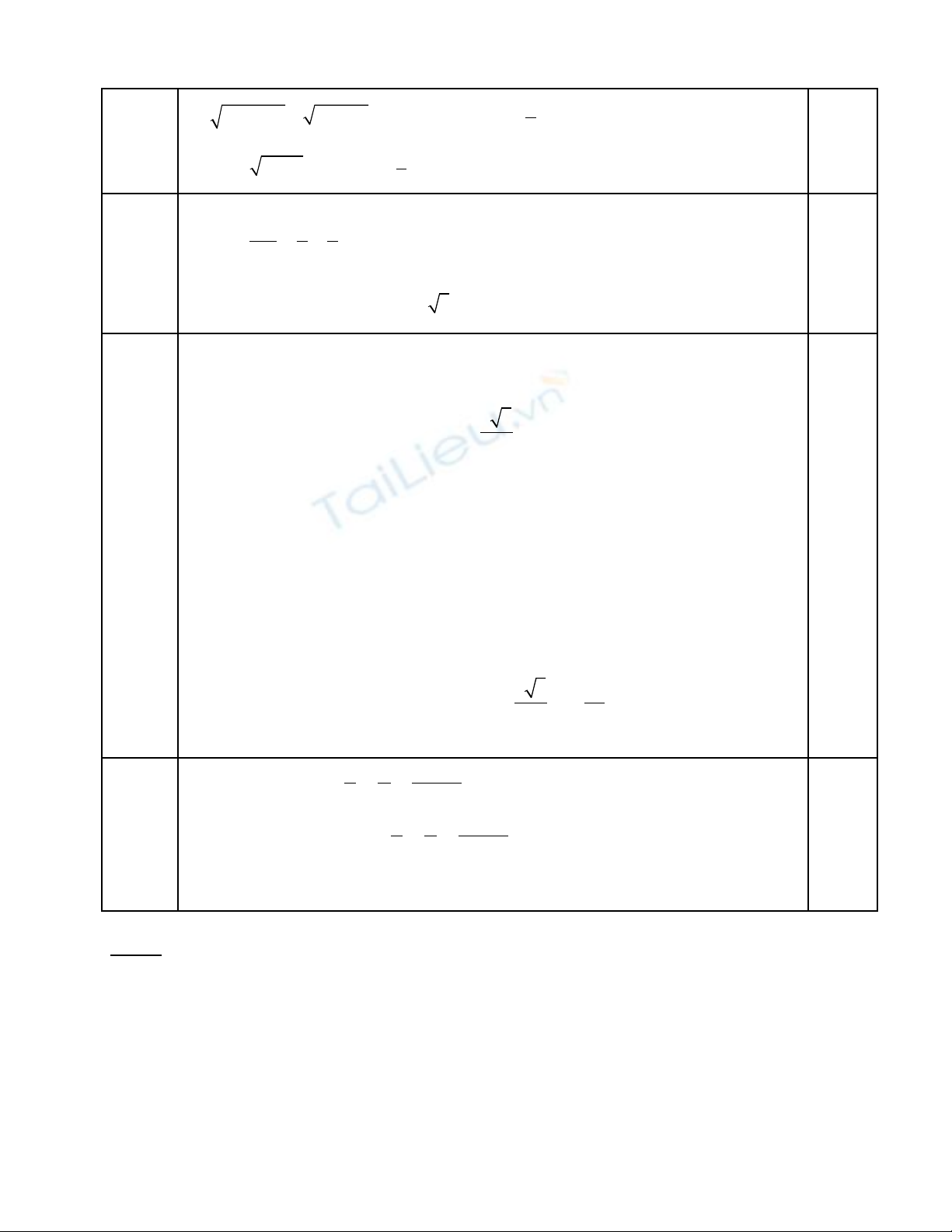
Câu 2 : ( 1,5 đi m ) Th c hi n phép tính.ể ự ệ
( )
2
3 2 2 3 5
) 20 45 2 80 c)
3 2 6 1
5 5 5 5
) 3 2 24 ) 5 5 5 5
−
+ − −
− −
+ −
− + +
− +
a
b d
Câu 3 : ( 2,0 đi m ) Cho bi u th c ể ể ứ
1 1
1 1
a a a a
Pa a
� �� �
+ −
= + −
� �� �
� �� �
+ −
� �� �
a. Tìm đi u ki n c a a đ bi u th c P có nghĩa.ề ệ ủ ể ể ứ
b. Rút g n bi u th c P.ọ ể ứ
c. Tìm a đ P= ể
1
4
Câu 4 : ( 1,5 đi m ) Gi i các ph ng trìnhể ả ươ
a.
2
(2 3) 5x+ =
b.
9(3 1) 12 4 10x x− + − =
Câu 5 : ( 3,0 đi m ) Cho tam giác ABC vuông t i A, đ ng cao AH, AB = 3cm, BC = 6cm.ể ạ ườ
1/ Gi i tam giác vuông ABCả
2/ G i E, F l n l t là hình chi u c a H trên c nh AB và AC:ọ ầ ượ ế ủ ạ
a/ Tính đ dài AH và ch ng minh: EF = AH.ộ ứ
b/ Tính: EA
EB + AF
FC
Câu 6 : (0,5 đi m)ểCho x > 0; y > 0. Ch ng minh r ng ứ ằ
yx
yxyx ;
411 ∀
+
≥+
H NG D N CH M Đ KI M TRA GI A KÌ IƯỚ Ẫ Ấ Ề Ể Ữ
L P 9Ớ
Năm h c: 2014 – 2015ọ
Môn: TOÁN
Th i gian làm bài 60 phútờ
Câu Đáp án Đi mể
Câu 1
1,5
đi mể
0,5
Phát bi u đúngể
Tìm đ c m ≠ 5, m ≠ -3 0.5ượ
Tìm đ c m <0,2 0,5ượ
Câu 2
1,5
đi mể
a. =
2 5 3 5 8 5+ −
= (2 + 3 – 8 ).
= -3
b.=
( ) ( )
2 2
3 2 6 3 4.6− + +
= 3 - 2
6
+2 +2
6
= 5
3 2 2 3 5
c) 3 2 6 1
−−
− −
6( 3 2 ) 5
3 2 6 1
−
= −
− −
6 6 5
6 1
− −
=−
( 6 1) 1
6 1
− −
= = −
−
0,5
0,5
0,5
Câu 3
2,0
đi mể
a.
0, 1a a
b.
( ) ( )
1 1
1 1
( 1) ( 1)
1 1
1 1
1 1
1
a a a a
Pa a
a a a a
a a
a a
a
� �� �
+ −
= + −
� �� �
� �� �
+ −
� �� �
� �� �
+ −
= + −
� �� �
� �� �
+ −
� �� �
= + −
= −
c. a=
3
4
0.5
1.0
0,5
Câu 4
1,5
a) x= 1; x=-4 0,75
đi mểb)
9(3 1) 12 4 10x x− + − =
(ĐKXĐ):
1
3
x
5
5 3 1 10 3
x x− = =� �
0,75
Câu 5
3,0
đi mể
1. +
∆
ABC vuông t i A, nên:ạ
cosB =
AB 3 1
BC 6 2
= =
góc B
0
60=
Do đó: góc C
0 0 0
90 60 30= − =
AC = BC
sinB = 6
sin600 =
3 3
cm
0.5
0.5
0.5
2. G i E, F l n l t là hình chi u c a H trên c nh AB và AC:ọ ầ ượ ế ủ ạ
a/ Tính đ dài AH và ch ng minh EF = AH ộ ứ
∆
AHB vuông t i H nên: ạ
AH = AB.sinB = 3.sin600 =
3 3
2
cm
T giác AEHF có: Góc A = góc E = góc F = 90ứ0 (gt)
Nên t giác AEHF là hình ch nh tứ ữ ậ
EF = AH
b/ Tính: EA
EB + AF
FC
Ta có: EA
EB = HE2 ; AF
FC = FH2
Nên EA
EB + AF
FC = HE2 + FH2 = EF2
Mà EF = AH (cmt)
Do đó: EA
EB + AF
FC =AH2 =
2
3 3 27 6,75
2 4
� �= =
� �
� �
� �
cm
0.5
0.25
0.25
0.5
Câu 6
0,5
đi mể
Vì x > 0; y > 0 nên
yxyx +
≥+ 411
⇔
...
⇔
(x – y)2
≥
0
V y n u x > 0; y > 0 thì ậ ế
yx
yxyx ;
411 ∀
+
≥+
.
D u “=” x y ra khi và ch khi x = y.ấ ả ỉ
0,5
L u ýư: HS gi i cách khác đúng v n đ c h ng đi m t i đa.ả ẫ ượ ưở ể ố