Đề số 2
Câu 1. Tìm các số thực
;xy
để
22x i yi− = +
.
A.
2; 2xy==
. B.
2; 2xy= = −
. C.
2; 2xy= − = −
. D.
2; 2xy= − =
.
Câu 2. Cho hai số phức
12
3 4 ; 4 3z i z i= − + = +
. Môđun của số phức
là:
A.
50
. B.
8
. C.
50
. A.
8
.
Câu 3. Nghịch đảo của số phức
12zi=−
A.
12
55
i+
. B.
12
.
55
i−
C.
1 2 .i+
D.
1 2 .i−−
Câu 4. Tìm các số thực
,xy
sao cho
( ) ( ) ( )
2 4 2 2x y x y i x y yi− + + + = + +
A.
3; 1.xy= − =
B.
3; 1.xy==
C.
3; 1.xy= = −
D.
3; 1.xy= − = −
Câu 5. Số nào trong các số phức sau là số thuần ảo?
A.
3i−
. B.
2i−
. C.
2
. D.
1i+
.
Câu 6. Giá trị của biểu thức
2 3 2017
1 ....A i i i i= + + + + +
là
A.
1i+
. B.
0
. C.
i
. D.
1i−
.
Câu 7. Cho số phức
z
khác
0
. Biết rằng nghịch đảo của số phức
z
bằng một nửa số phức liên hợp của
nó. Mệnh đề nào đúng ?
A.
2z=
. B.
1
2
z=
. C.
1
2
z=
. D.
2z=
.
Câu 8. Tìm số phức
z
biết
( )
2 4 0iz− − =
A.
84
55
zi=−
. B.
84
55
zi=+
. C.
48
55
zi=+
. D.
48
55
zi=−
.
Câu 9. Cho các số phức bất kì
, ' ' 0z z z
. Xét các mệnh đề sau:
: . ' . 'a z z z z
,
''b z z z z
,
''c b z z z z
và
''
z
z
dzz
. Có bao nhiêu mệnh đề sai?
A.
2
. B.
1
. C.
4
. D.
0
.
Câu 10. Cho số phức
2zi
. Tìm tọa độ của điểm biểu diễn số phức
z
.
A.
( )
2; 1N−
. B.
( )
1,2M−
. C.
( )
2;1P
. D.
( )
1;2Q
.
Câu 11. Trong mặt phẳng tọa độ
Oxy
, gọi
;;A B C
lần lượt là các điểm biểu diễn các số phức
1 2 3
3 4 ; 2 ; 8 2z i z i z i= − = + = −
. Giả sử
G
là trọng tâm tam giác
ABC
thì tọa độ điểm
G
là:
A.
5
1; 3
G


. B.
( )
3;5G
. C.
13 5
;
33
G


. D.
5;1
3
G


.
Câu 12. Tập hợp các điểm biểu diễn các số phức thỏa mãn
34z z i= − +
là:
A. Đường thẳng
6 8 25xy+=
. B. Đường thẳng
3 4 2xy+=
.
C. Đường thẳng
4 2 2xy−=
. D. Đường thẳng
6 8 25xy−=
.
Câu 13. Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
22zi+ + =
là đường tròn có tâm và bán kính
lần lượt là:
A.
( )
2; 1 ; 2IR− − =
. B.
( )
2;1 ; 2IR=
. C.
( )
2;1 ; 2IR=
. D.
( )
2; 1 ; 2IR− − =
.
Câu 14. Tìm các số thực
,ab
để phương trình
20z az b+ + =
có một nghiệm là
2zi=−
, trong đó
i
là
đơn vị ảo của tập số phức.
A.
4; 5ab= − =
. B.
5; 4ab= = −
. C.
8; 12ab==
. D.
12; 8ab==
.
Câu 15. Gọi
12
,zz
là hai nghiệm phức của phương trình
22 2 0zz
. Tính giá trị biểu thức
1 2 1 2
2P z z z z
.
A.
6
. B.
2 2 2
. C.
2 2 4
. D.
3
.
Câu 16. Giả
12
,zz
là hai nghiệm của phương trình
23 2 2 4 0z i z i
.Gọi
;AB
là điểm biểu diễn
của các số phức
12
,zz
trên mặt phẳng tọa độ. Tính
OAB
S
.
A.
2
. B.
4
. C.
1
. D.
8
.
Câu 17. Cho số phức
z
khác
0
thỏa mãn
( )
3 . 1 2 6z z z z iz+ = +
. Khi đó,
z
bằng:
A.
1
13
. B.
13
. C.
15
. D.
1
15
.
Câu 18. Cho
S
là diện tích hình phẳng giới hạn bởi các đường
lnyx=
,
1x=
,
xe=
và trục
Ox
. Khi
đó:
A.
1
ln d
e
S x x=
. B.
2
1
ln d
e
S x x
=
. C.
1
ln d
e
S x x
=
. D.
2
1
ln d
e
S x x=
.
Câu 19. Hình phẳng được giới hạn bởi các đường
311 6y x x= + −
,
2
6yx=
,
0x=
và
2x=
có diện tích
là:
A.
5
2
. B.
2
. C.
9
4
. D.
33
4
.
Câu 20. Diện tích hình phẳng được giới hạn bởi các đường
sinyx=
,
x
=−
và
x
=
và trục
.Ox
là:
A.
4
. B.
2
. C.
6
. D.
3
.
Câu 21. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường
2
4yx=−
,
0y=
quay quanh trục
.Ox
bằng:
A.
512
15
. B.
512
15
. C.
16
3
. D.
16
3
.
Câu 23. Cho hình vẽ bên, diện tích hình phẳng (phần gạch sọc) là:
A.
( ) ( ) ( ) ( )
0.
b
ab
S g x f x dx f x g x dx= − + −

B.
( ) ( ) ( ) ( )
0.
b
ab
S g x f x dx f x g x dx

= − + −

C.
( ) ( ) ( ) ( )
0.
b
ab
S f x g x dx g x f x dx= − + −

D.
( ) ( ) ( ) ( )
0.
b
ab
S f x g x dx g x f x dx

= − + −

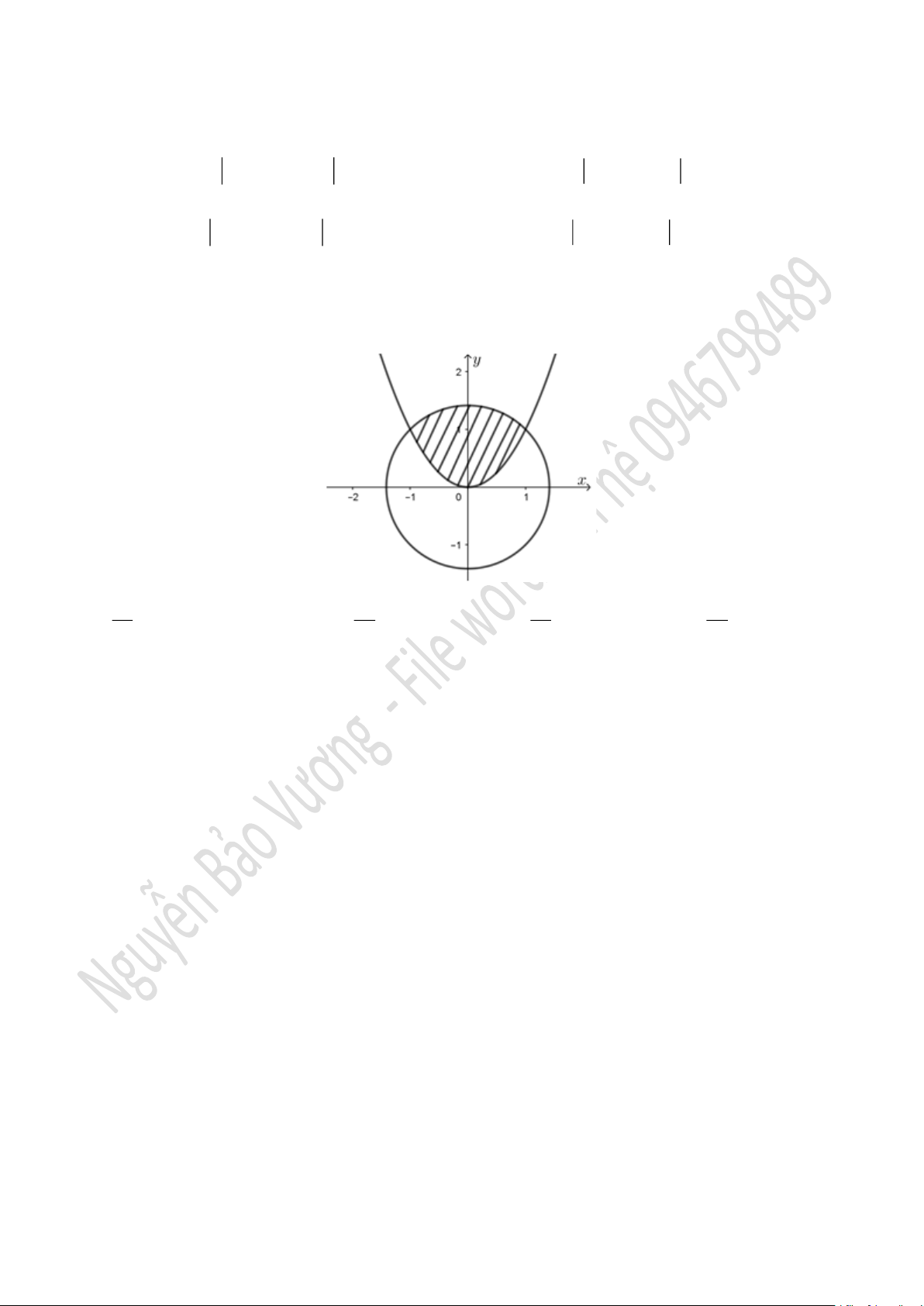
Câu 24. Cho các hàm số
( ) ( )
;y f x y g x==
liên tục và không âm trên đoạn
;.ab
Hình phẳng giới hạn
bởi các đường
( ) ( )
; ; ;y f x y g x x a x b= = = =
quay quanh trục
Ox
tạo ra khối tròn xoay có thể
tích tính theo công thức.
A.
( ) ( )
22
.
b
a
V f x g x dx
=−
B.
( ) ( )
.
b
a
V f x g x dx
=−
C.
( ) ( )
22
.
b
a
V f x g x dx=−
D.
( ) ( )
.
b
a
V f x g x dx=−
Câu 25. Cho
( ) ( )
2 2 2
: ; : 2P y x C x y= + =
. Cho phần hình phẳng (gạch chéo trên hình vẽ) quay xung
quanh trục
Ox
sinh a khối tròn xoay có thể tích bằng:
A.
44
15
. B.
44
15
. C.
22
15
. D.
22
15
.
Lời giải tham khảo
Câu 1. Tìm các số thực
;xy
để
22x i yi− = +
.
A.
2; 2xy==
. B.
2; 2xy= = −
. C.
2; 2xy= − = −
. D.
2; 2xy= − =
.
Lời giải
Chọn A
Ta có:
2
2 2 2 2 2
x
x i yi x i yi y
=
− = + + = + =
.
Câu 2. Cho hai số phức
12
3 4 ; 4 3z i z i= − + = +
. Môđun của số phức
là:
A.
50
. B.
8
. C.
50
. A.
8
.
Lời giải
Chọn A
Ta có:
( ) ( )
12 3 4 4 3 1 7z z z i i i= + = − + + + = +
.
Do đó:
22
1 7 1 7 50zi= + = + =
.
Câu 3. Nghịch đảo của số phức
12zi=−
A.
12
55
i+
. B.
12
.
55
i−
C.
1 2 .i+
D.
1 2 .i−−
Lời giải
Chọn A
Ta có :
( )( )
1 1 1 2 1 2 1 2 .
1 2 1 2 1 2 5 5 5
ii
wi
z i i i
++
= = = = = +
− − +
Câu 4. Tìm các số thực
,xy
sao cho
( ) ( ) ( )
2 4 2 2x y x y i x y yi− + + + = + +
A.
3; 1.xy= − =
B.
3; 1.xy==
C.
3; 1.xy= = −
D.
3; 1.xy= − = −
Lời giải
Chọn A
Ta có :
( ) ( ) ( )
2 2 3 0 3
2 4 2 2 4 2 4 1
x y x y x y x
x y x y i x y yi x y y x y y
− = + + = = −
− + + + = + +
+ + = − = − =
Câu 5. Số nào trong các số phức sau là số thuần ảo?
A.
3i−
. B.
2i−
. C.
2
. D.
1i+
.
Lời giải
Chọn A
Số thuần ảo có phần thực
0a=
.
Câu 6. Giá trị của biểu thức
2 3 2017
1 ....A i i i i= + + + + +
là
A.
1i+
. B.
0
. C.
i
. D.
1i−
.
Lời giải
Chọn A
Ta có:
2 3 2017
1 ....A i i i i= + + + + +
=
2018
1
1. 1ii
−
−
( )
( )
2018
11
2
ii−+
=
2018 2019
12
i i i+ − −
=
( ) ( )
1009 1009
22
1.
2
i i i i+ − −
=
1i=+
.
(Chú ý:
2 3 2017
1 ....i i i i+ + + + +
là tổng của CSN có 2018 số hạng , số hạng đầu
11; )u q i==
Câu 7. Cho số phức
z
khác
0
. Biết rằng nghịch đảo của số phức
z
bằng một nửa số phức liên hợp của
nó. Mệnh đề nào đúng ?
A.
2z=
. B.
1
2
z=
. C.
1
2
z=
. D.
2z=
.
Lời giải
Chọn A
Theo đề bài ta có:
2
1. 2 2 2.
2
zz z z z
z= = = =
Câu 8. Tìm số phức
z
biết
( )
2 4 0iz− − =
A.
84
55
zi=−
. B.
84
55
zi=+
. C.
48
55
zi=+
. D.
48
55
zi=−
.
Lời giải
Chọn A
Ta có :
( )
2 4 0iz− − =
4 8 4
2 5 5
zi
i
= = +
−
84
55
zi = −
.
Câu 9. Cho các số phức bất kì
, ' ' 0z z z
. Xét các mệnh đề sau:
: . ' . 'a z z z z
,
''b z z z z
,
''c b z z z z
và
''
z
z
dzz
. Có bao nhiêu mệnh đề sai?
A.
2
. B.
1
. C.
4
. D.
0
.
Lời giải
Chọn A
mệnh đề đúng là
,ad
. Mệnh đề sai là
,bc
.
Câu 10. Cho số phức
2zi
. Tìm tọa độ của điểm biểu diễn số phức
z
.
A.
( )
2; 1N−
. B.
( )
1,2M−
. C.
( )
2;1P
. D.
( )
1;2Q
.
Lời giải
Chọn A
Ta có
2zi
do đó tọa độ điểm biểu diễn số phức đó là
2; 1N
.
Câu 11. Trong mặt phẳng tọa độ
Oxy
, gọi
;;A B C
lần lượt là các điểm biểu diễn các số phức
1 2 3
3 4 ; 2 ; 8 2z i z i z i= − = + = −
. Giả sử
G
là trọng tâm tam giác
ABC
thì tọa độ điểm
G
là:
A.
5
1; 3
G


. B.
( )
3;5G
. C.
13 5
;
33
G


. D.
5;1
3
G


.
Lời giải