ĐỀ SỐ 19
Câu 1: Cho hàm số
322
23
33
x
y x x= − + +
. Toạ độ điểm cực đại của đồ thị hàm số là
A.
( )
1;2−
. B.
( )
1;2
. C.
( )
1; 2−
. D.
2
3;3



.
Câu 2: Hm số
( )
y f x=
c đạo hm l
22
'( ) ( 1) (2 1)f x x x x= + −
. Số điểm cực trị của hm số l:
A.
B.
1.
C.
2.
D.
3.
Câu 3: Hm số
32
21
32
xx
yx= + − −
đạt giá trị nhỏ nhất trên
0;2
là:
A.
1
3
−
. B.
13
6
−
. C.
1−
. D.
4−
.
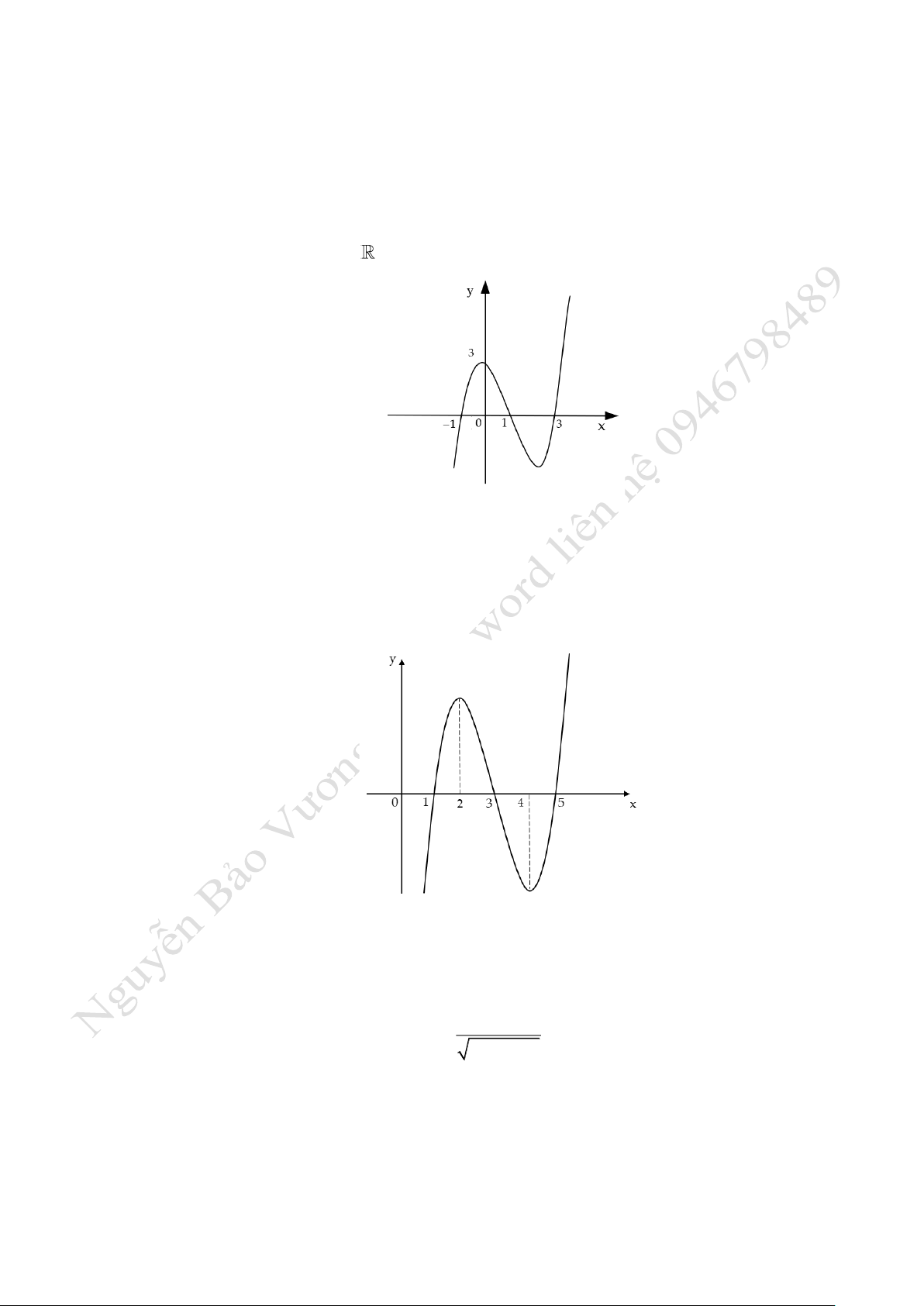
Câu 4: Đường cong ở hình vẽ l đồ thị của một trong các hm số dưới đây. Hm số đ l hm số no?
A.
( )( )
2
12y x x= − +
. B.
( ) ( )
2
12y x x= − +
.
C.
( )( )
2
12y x x= − −
. D.
( ) ( )
2
12y x x= + +
.
Câu 5: Tính giá trị cực tiểu
CT
y
của hàm số
42
23y x x= − +
.
A.
2.
CT
y=
B.
1.
CT
y=−
C.
3.
CT
y=
D.
1.
CT
y=
Câu 6: Giá trị lớn nhất của hàm số
21mx
ymx
+
=−
trên đoạn
2;3
là
5
4
khi m nhận giá trị bằng:
A.
5−
B. 1. C.
2−
. D.
1.−
Câu 7: Các khoảng nghịch biến của hàm số
312 12y x x= − +
là:
A.
( )
;2− −
. B.
( )
2;2−
. C.
( ) ( )
; 2 ; 2;− − +
. D.
( )
2;+
.
Câu 8: Hàm số
( ) ( )
32
11 1 1
3
y x m x m x= + + − + +
đồng biến trên tập xác định của nó khi:
A.
21m− −
. B.
12m−
. C.
21m−
. D.
21m− −
.
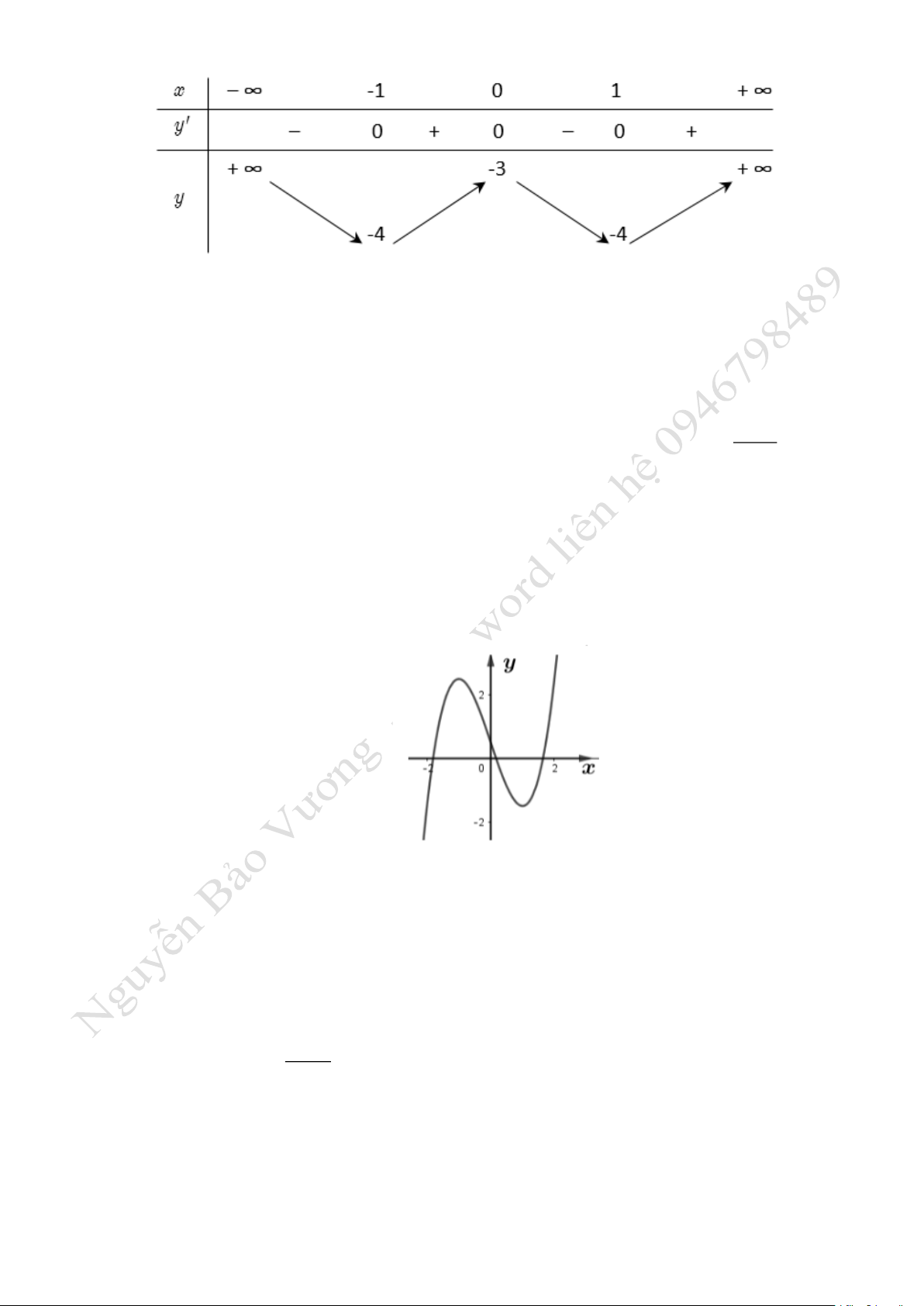
Câu 9: Cho hm số
( )
y f x=
xác định, liên tục trên v c bảng biến thiên dưới đây:
Mệnh đề no sau đây đúng?
A. Hm số đạt cực đại tại
1x=
.
B. Hm số có
2
điểm cực đại.
C. Hm số c
3
điểm cực trị.
D. Hm số nghịch biến trên khoảng
( )
1;0−
.
Câu 10: Kí hiệu
,mM
lần lượt l giá trị nhỏ nhất vgiá trị lớn nhất của hm số
3
21
x
yx
+
=−
trên đoạn
1;4
. Tính giá trị biểu thức
d M m=−
.
A.
4d=
. B.
5d=
. C.
2d=
. D.
3d=
.
Câu 11: Hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x=
khi:
A.
0m
. B.
0m
. C.
0m=
. D.
0m
.
Câu 12: Một hàm số
32
( ) ,( 0)y f x ax bx cx d a= = + + +
c đồ thị như hình dưới đây
Phương trình
2
5 2 ( ) 2f x m− = +
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 13: Hm số
42
2 4 1y x x= − −
đồng biến trên những khoảng no?
A.
( )
;1− −
và
( )
0;1
. B.
( )
1;0−
và
( )
1; +
.
C.
( )
1;1 \ 0−
. D.
( )
;1− −
và
( )
1; +
.
Câu 14: Đồ thị hm số
32
1
x
yx
−
=−
c đường tiệm cận đúng, tiệm cận ngang l:
A.
1; 2xy==
. B.
1; 2xy= − = −
. C.
2; 1xy==
. D.
1; 2xy= = −
.
Câu 15: Một hm số
( )
32 0y ax bx cx d, a= + + +
c đồ thị như hình dưới đây
Chọn phát biểu đúng trong các phát biểu dưới đây?
A.
00a ,c
B.
00a ,c
C.
0 0 0a ,b ,c
D.
00a ,c
Câu 16: Phương trình tiếp tuyến của (C):
1
1
x
yx
+
=−
tại giao điểm với trục honh l:
A.
( )
11
2
yx= − +
B.
( )
11
2
yx= − −
C.
( )
11
2
yx=−
D.
( )
11
2
yx=+
Câu 17: Một ngọn hải đăng đặt ở vị trí
A
cách bờ
5km
, trên bờ biển c một kho hng ở vị trí
C
cách
B
một khoảng
7km
. Người canh hải đăng c thể chèo thuyền từ
A
đến
M
trên bờ biển với
vận tốc
4/km h
rồi đi bộ từ
M
đến
C
với vận tốc
6/km h
. Xác định độ di đoạn
BM
để
người đ đi từ
A
đến
C
nhanh nhất.
A.
7
2km
. B.
25km
. C.
32km
. D.
7
3km
.
Câu 18: Cho hm số
( )
=y f x
c đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số
m
để phương
trình
( )
=−2f x m
c bốn nghiệm phân biệt.
A.
− −21m
. B.
− −43m
. C.
− −43m
. D.
− −21m
.
Câu 19: Cho hm số
32
32y x x= − + −
c đồ thị
( )
C
. Số tiếp tuyến với đồ thị
( )
C
song song với đường
thẳng
97yx= − −
là:
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 20: Đồ thị hm số
42
2y x x= − + +
cắt
Oy
tại điểm
A.
( )
2;0A
. B.
( )
0;0O
. C.
( )
0; 2A−
. D.
( )
0;2A
.
Câu 21: Cho hàm
( )
fx
liên tục trên v hình dưới đây l đồ thị của hàm
( )
=y f x
Tìm các khoảng đồng biến của hàm
( )
=y f x
?
A.
( )
;1− −
;
( )
3;+
B.
( )
1;0−
;
( )
1;3
C.
( )
1;1−
;
( )
3;+
D.
( )
;0−
;
( )
3;+
Câu 22: Cho hàm số
( )
=y f x
. Biết
( )
fx
c đạo hàm
( )
'fx
và hàm số
( )
=y f x
c đồ thị như hình
vẽ. Hàm số
( ) ( )
1=−g x f x
đạt cực đại tại điểm no dưới đây?
A.
3.=x
B.
2.=x
C.
4=x
D.
1.=x
Câu 23: Số giao điểm của đồ thị hm số
( )
( )
23 10 3y x x x= − + +
v trục honh l:
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 24: Số đường tiệm cận của đồ thị hm số
2
21
2
x
yxx
−
=++
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 25: Số giao điểm của hai đường cong
3
=−y x x
và
=−
2
y x x
là:
A. 0. B. 2. C. 1. D. 3.
BẢNG ĐÁP ÁN
1.B
2.B
3.B
4.B
5.A
6.D
7.B
8.A
9.C
10.D
11.C
12.B
13.B
14.D
15.A
16.A
17.B
18.A
19.D
20.D
21.C
22.A
23.D
24.B
25.D
LỜI GIẢI CHI TIẾT
Câu 1. Cho hàm số
322
23
33
x
y x x= − + +
. Toạ độ điểm cực đại của đồ thị hàm số là
A.
( )
1;2−
. B.
( )
1;2
. C.
( )
1; 2−
. D.
2
3;3



.
Lời giải
Chọn B
Ta có
24 3.y x x
= − +
1
0.
3
x
yx
=
=
=
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy đồ thị hàm số đạt cực đại tại điểm
( )
1;2
.
Câu 2. Hm số
( )
y f x=
c đạo hm l
22
'( ) ( 1) (2 1)f x x x x= + −
. Số điểm cực trị của hm số l:
A.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B
Cho
( )
'
0
01
1
2
x
f x x
x
=
= = −
=
.
Ta có bảng biến thiên:
x
−
1−
0
1
2
+
'y
−
0
−
0
−
0
+
Dựa vào bảng biên thiên ta thấy
( )
'
fx
chỉ đổi dấu
1
lần duy nhất khi đi qua điểm
1
2
x=
.
1
3
0
0
y
2
2
3
x
−
+
y
+
−
+
+
−
−