ĐỀ SỐ 4. ZALO 0946798489
Câu 1: Cho
( )
y f x=
và
( )
y g x=
là các hàm số đồng biến trên . Khẳng định nào là đúng?
A. Hàm số
( ) ( )
.y f x g x=
đồng biến trên . B. Hàm số
( ) ( )
y f x g x=−
đồng biến trên .
C. Hàm số
( ) ( )
y f x g x=+
đồng biến trên . D. Hàm số
( )
,0y kf x k=
đồng biến trên .
Câu 2: Giá trị nhỏ nhất của hàm số
42
23y x x= − −
bằng
A.
5−
. B.
2−
. C.
4−
. D.
3−
.
Câu 3: Tìm tập hợp tất cả các giá trị của
m
để phương trình
2
10
1
xm
xx
+−=
−+
có hai nghiệm phân
biệt.
A.
( )
;1−
. B.
1;2−
. C.
1;3−
. D.
( )
1;2
.
Câu 4: Cho hàm số
2
8yx=−
. Khẳng định nào sau đây là sai?
A. Hàm số đạt cực đại tại
0x=
. B. Hàm số đạt giá trị nhỏ nhất tại
22x=
.
C. Hàm số không có giá trị lớn nhất. D. Hàm số đạt giá trị lớn nhất bằng
22
.
Câu 5: Giá trị nhỏ nhất của hàm số
3sin 15 7y x x= + +
trên đoạn
0;
là
A.
7
. B.
5
. C.
17
. D.
7
+
.
Câu 6: Cho hàm số
32
71y x x x= − + −
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên .
B. Hàm số đồng biến trên
( )
0;+
và nghịch biến trên
( )
;0−
.
C. Hàm số đồng biến trên
( )
;0−
và nghịch biến trên
( )
0;+
.
D. Hàm số nghịch biến trên .
Câu 7: Cho hàm số
( )
y f x=
và hàm số
( )
y g x=
xc định trên
;ab
. Biết
( )
;
max
ab f x M=
và
( )
;
max
ab g x N=
. Khẳng định nào dưới đây là đúng?
A.
( ) ( )
;
max
ab f x g x M N− = −
. B.
( ) ( )
;
max
ab f x g x M N+ = +
.
C.
( )
;
max4 4
ab f x M=
. D.
( )
;
max
ab kf x kM=
.
Câu 8: Biết rằng hàm số
( )
2
2 7 5
3
x x k
fx x
− + −
=+
đạt cực trị tại cc điểm
1
x
,
2
x
. Gi trị của biểu thc
( ) ( )
12
12
f x f x
Pxx
−
=−
là
A. 6. B. 3. C. 2. D. 4.
Câu 9: Cho hàm số
()y f x=
liên tục trên và có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
1x=−
. B. Hàm số đạt giá trị lớn nhất bằng
5
.
C. Hàm số đạt giá trị nhỏ nhất bằng
2−
. D. Hàm số không có cực trị.
Câu 10: Một động tử chuyển động trên tia
Ox
với quãng đường đi được tính theo công thc
32
15 28
3
s t t t= − +
, với
t
là thời gian tính bằng giây,
0 20t
và
s
tính bằng mét. Hỏi sau bao
nhiêu giây tính từ lúc động tử bắt đầu chuyển động, vận tốc của nó đạt giá trị nhỏ nhất?
A.
6
. B.
3
. C.
4
. D.
5
.
Câu 11: Biết rằng hàm số
312 1234y x x= − +
đạt cực trị tại
12
,xx
. Khi đó hiệu
12
xx−
là
A. 1. B. 4. C. 3. D. 2.
Câu 12: Giá trị nhỏ nhất của hàm số
32
3 20y x x= − +
trên đoạn
1;5−
là
A.
16
. B.
17
. C.
19
. D.
20
.
Câu 13: Có bao nhiêu giá trị nguyên của
m
để hàm số
4 3 2
8 3(2 1) 13y x mx m x= − − − + +
chỉ có cực đại
mà không có cực tiểu?
A. 0 B. 3 C. 2 D. 1
Câu 14: Cho hàm số
3sin 4cos 7 13y x x x= − − +
. Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( ;0)−
và nghịch biến trên khoảng
(0; )+
.
B. Hàm số đồng biến trên .
C. Hàm số nghịch biến trên .
D. Hàm số đồng biến trên khoảng
( 1;1)−
.
Câu 15: Đồ thị hàm số
( )
2
2
7
9
x
yxx
+
=−
có mấy đường tiệm cận?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 16: Đồ thị hàm số
28 15
2
xx
yx
−+
=−
cắt trục hoành tại mấy điểm?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 17: Cho
,ab
là các số thực thuộc khoảng
0; 2
và thỏa mãn điều kiện
cot cota b a b− = −
. Giá trị
của biểu thc
37ab
Pab
+
=+
bằng
A. 3. B. 6. C. 4. D. 5.
Câu 18: Tìm tất cả các giá trị của
k
để hàm số
( )
32
16 5 7 11
3
y x kx k x k= − + + − − +
nghịch biến trên .
A.
(
)
;2 3;− +
. B.
2;3−
. C.
2;3
. D.
3; 2−−
.
Câu 19: Cho hàm số
( )
y f x=
có bảng biến thiên:

Phương trình
( )
0f x m−=
có ba nghiệm phân biệt khi và chỉ khi
A.
37m−
. B.
17m−
. C.
7m
. D.
1m−
.
Câu 20: Cho hàm số
32
1
x
yx
−
=−
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
\1
.
B. Hàm số nghịch biến trên mỗi khoảng
( )
;1−
và
( )
1; +
.
C. Hàm số đồng biến trên khoảng
( )
1; +
.
D. Hàm số nghịch biến trên khoảng
( )
3;5−
.
Câu 21: Đồ thị hàm số
62
4
x
yx
−
=+
có mấy đường tiệm cận?
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 22: Đồ thị hàm số
42
129 135y x x= − −
cắt trục tung tại điểm
M
. Độ dài
OM
bằng?
A.
137
. B.
136
. C.
134
. D.
135
.
Câu 23: Hàm số
3
5 12 120y x x= − − +
có mấy điểm cực trị?
A. 0. B. 1. C. 2. D. 3.
Câu 24: Biết rằng hàm số
( )
3 2 4 2
14 1 9
3
y x x m m x= − − + + −
có hai điểm cực trị
12
;xx
. Tính tổng
12
xx+
?
A. 4. B. 8. C. 2. D. 10.
Câu 25: Cho
n
là số tự nhiên chẵn và
a
là số thực lớn hơn
3
. Phương trình
( ) ( )
2 1 2
1 3 2 0
n n n
n x n x a
+ + +
+ − + + =
có mấy nghiệm?
A.
2
. B.
1
. C. 4. D. 0.
HẾT

BẢNG ĐÁP ÁN
1.C
2.C
3.D
4.C
5.A
6.A
7.C
8.D
9.B
10.D
11.B
12.A
13.D
14.C
17.A
18.C
19.B
20.B
21.A
22.D
23.A
24.B
25.D
LỜI GIẢI THAM KHẢO
Câu 1. Cho
( )
y f x=
và
( )
y g x=
là các hàm số đồng biến trên . Khẳng định nào là đúng?
A. Hàm số
( ) ( )
.y f x g x=
đồng biến trên . B. Hàm số
( ) ( )
y f x g x=−
đồng biến trên .
C. Hàm số
( ) ( )
y f x g x=+
đồng biến trên . D. Hàm số
( )
,0y kf x k=
đồng biến trên .
Lời giải
Chọn C
Cách 1
+ Hàm số
( ) ( )
.y f x g x=
có
( ) ( ) ( ) ( )
..y f x g x f x g x
=+
chưa thể kết luận
Đp n A sai.
+ Hàm số
( ) ( )
y f x g x=−
có
( ) ( )
y f x g x
=−
chưa thể kết luận
Đp n B sai.
+ Hàm số
( )
y f x=
và
( )
y g x=
là các hàm số đồng biến trên thì
( ) ( )
0; 0;f x g x x
;
( ) ( )
0; 0f x g x
==
tại hữu hạn điểm.
Khi đó hàm số
( ) ( )
y f x g x=+
có
( ) ( )
0,y f x g x x
= +
,
0y=
tại hữu hạn điểm nên
hàm số đồng biến trên . Đp n C đúng.
+ Hàm số
( )
,0y kf x k=
có
( )
,0y kf x k
=
. Hàm số đồng biến trên khi
0k
, nghịch
biến trên khi
0k
. Vậy đáp án D sai.
Cách 2
- Đp n A sai. Ví dụ cho
( )
f x x=
và
( )
g x x=
là các hàm số đồng biến trên mà hàm số
( ) ( )
2
.y f x g x x==
không đồng biến trên .
- Đp n B sai. Ví dụ cho
( )
f x x=
và
( )
g x x=
là các hàm số đồng biến trên mà hàm số
( ) ( )
0y f x g x= − =
là hàm hằng trên .
- Đp n C đúng vì hàm số
( )
y f x=
và
( )
y g x=
là các hàm số đồng biến trên thì
( ) ( )
0; 0;f x g x x
;
( ) ( )
0; 0f x g x
==
tại hữu hạn điểm. Khi đó hàm số
( ) ( )
y f x g x=+
có
( ) ( )
0,y f x g x x
= +
,
0y=
tại hữu hạn điểm nên hàm số đồng
biến trên .
- Đp án D sai vì hàm số
( )
,0y kf x k=
có
( )
,0y kf x k
=
. Do đó, hàm số đồng biến trên
khi
0k
, nghịch biến trên khi
0k
.
Câu 2. Giá trị nhỏ nhất của hàm số
42
23y x x= − −
bằng
A.
5−
. B.
2−
. C.
4−
. D.
3−
.
Lời giải
Chọn C
Tập xc định
D=
.
Ta có
( )
32
4 4 4 1y x x x x
= − = −
.
( )
2
0 4 1 0y x x
= − =
0
1
1
x
x
x
=
=
=−
.
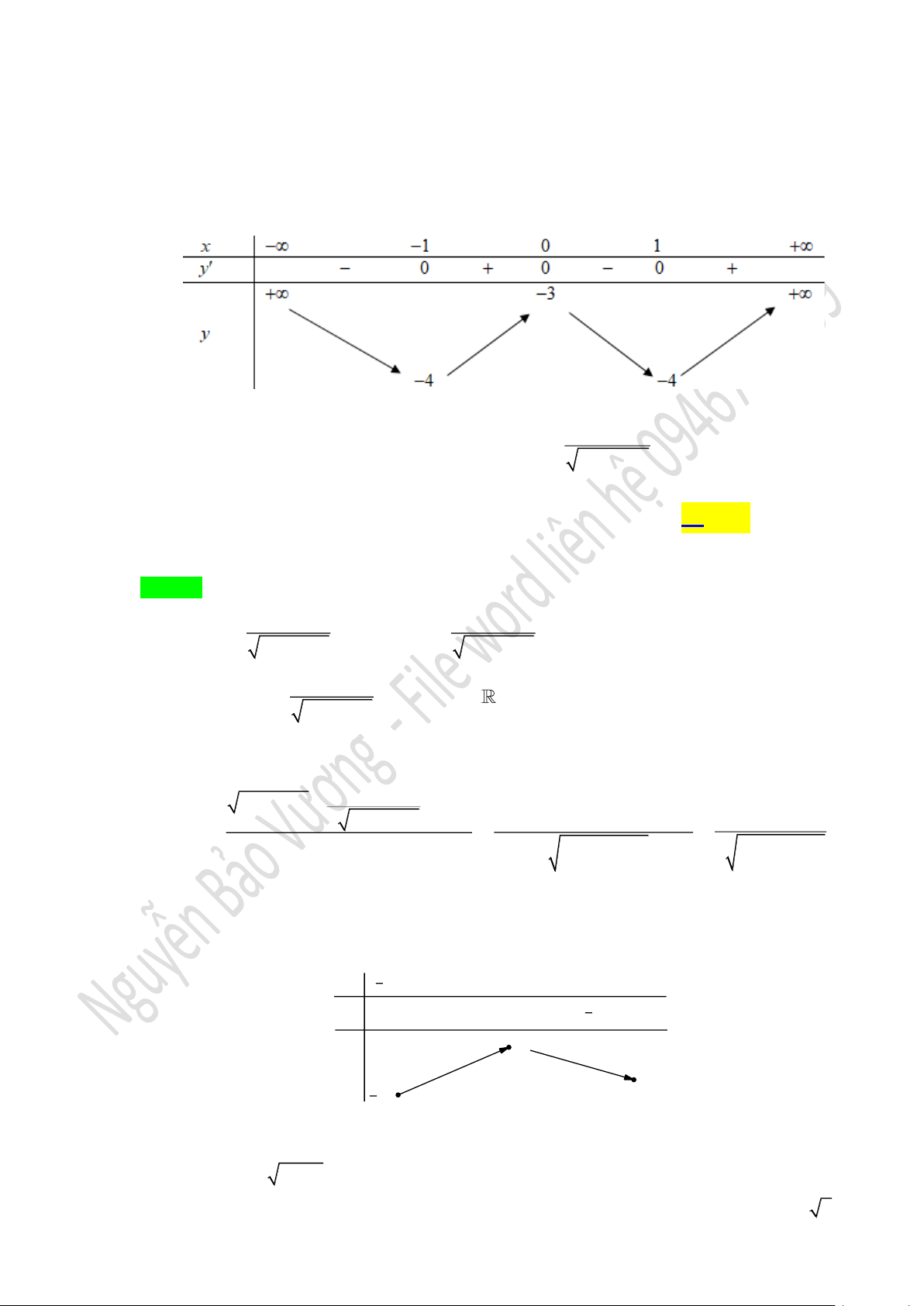
Bảng biến thiên
Từ bảng biến thiên, suy ra giá trị nhỏ nhất của hàm số đã cho bằng
4−
.
Câu 3. Tìm tập hợp tất cả các giá trị của
m
để phương trình
2
10
1
xm
xx
+−=
−+
có hai nghiệm phân
biệt.
A.
( )
;1−
. B.
1;2−
. C.
1;3−
. D.
( )
1;2
.
Lời giải
Chọn D
Phương trình
( )
22
11
0
11
xx
m m g x
x x x x
++
− = = =
− + − +
.
Xét hàm số
( )
2
1
1
x
gx xx
+
=−+
có TXĐ
D=
.
+)
( )
lim 1
xgx
→+ =
;
( )
lim 1
xgx
→− =−
.
+)
( )
( ) ( )
2
2
2
21
11
21
1
x
x x x
xx
gx xx
−
− + − +
−+
=−+
( ) ( )
( )
22
3
2
2 1 2 1
21
x x x x
xx
− + − + −
=
−+
( )
3
2
33
21
x
xx
−+
=
−+
.
( )
01g x x
= =
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình đã cho có hai nghiệm phân biệt
( )
1;2m
.
Câu 4. Cho hàm số
2
8yx=−
. Khẳng định nào sau đây là sai?
A. Hàm số đạt cực đại tại
0x=
. B. Hàm số đạt giá trị nhỏ nhất tại
22x=
.
1
1
2
∞
∞
+
+
1
g
g'
x
0



![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)







