ĐỀ SỐ 11
Câu 1. Thể tích khối nón có chiều cao bằng
h
, đường sinh bằng
l
là:
A.
2
1
3lh
B.
( )
22
1
3l h h
−
C.
22
l l h
−
D.
( )
22
l h h
−
Câu 2. Tính thể tích
V
của khối nón có diện tích hình tròn đáy là
S
và chiều cao là
h
.
A.
4
3
=V Sh
. B.
2
1
3
=V Sh
. C.
=V Sh
. D.
1
3
=V Sh
.
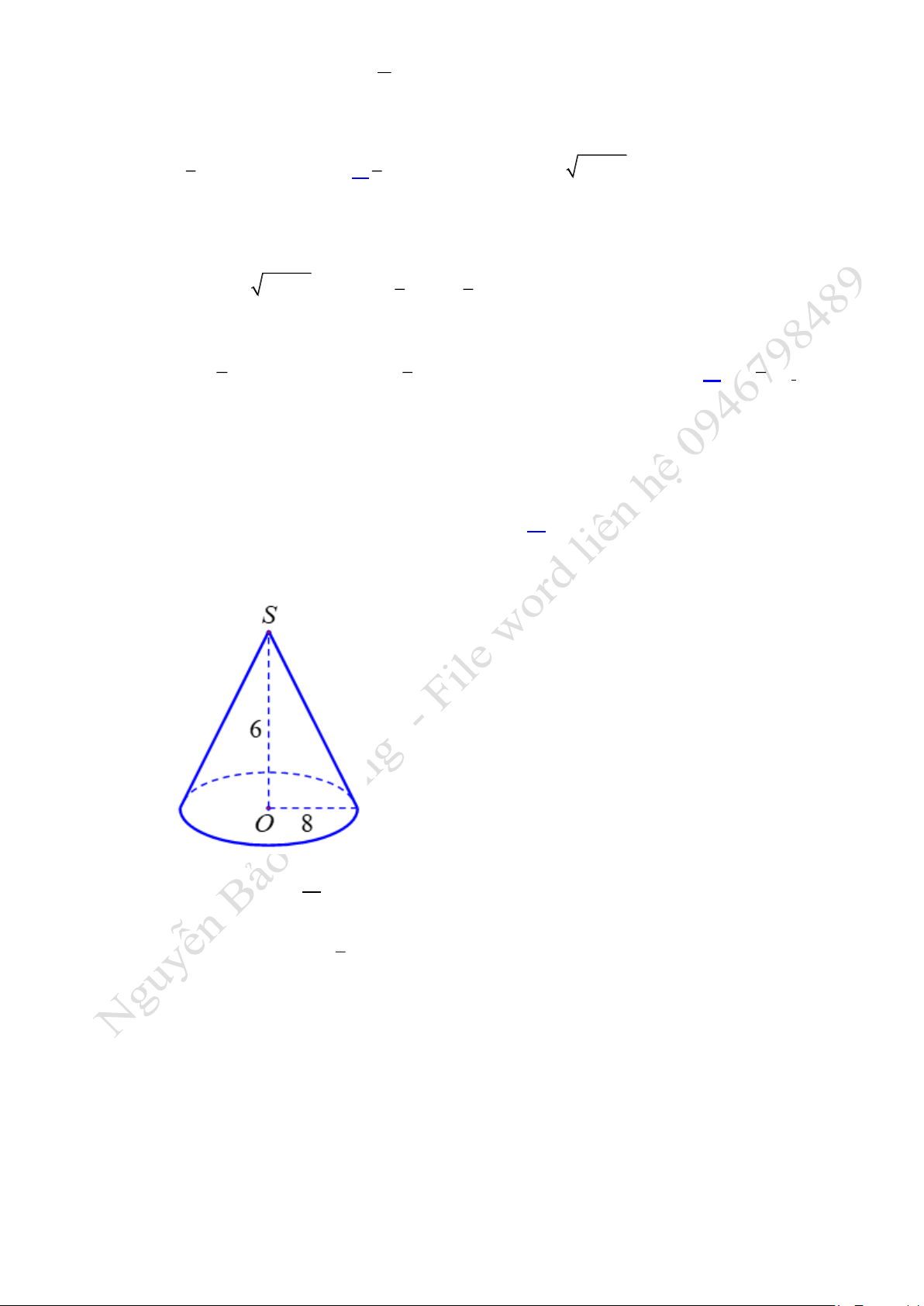
Câu 3. Tính thể tích của khối nón tròn xoay có chiều cao bằng
6
và đường kính đường tròn đáy bằng
16
.
A.
144
. B.
160
. C.
128
. D.
120
.
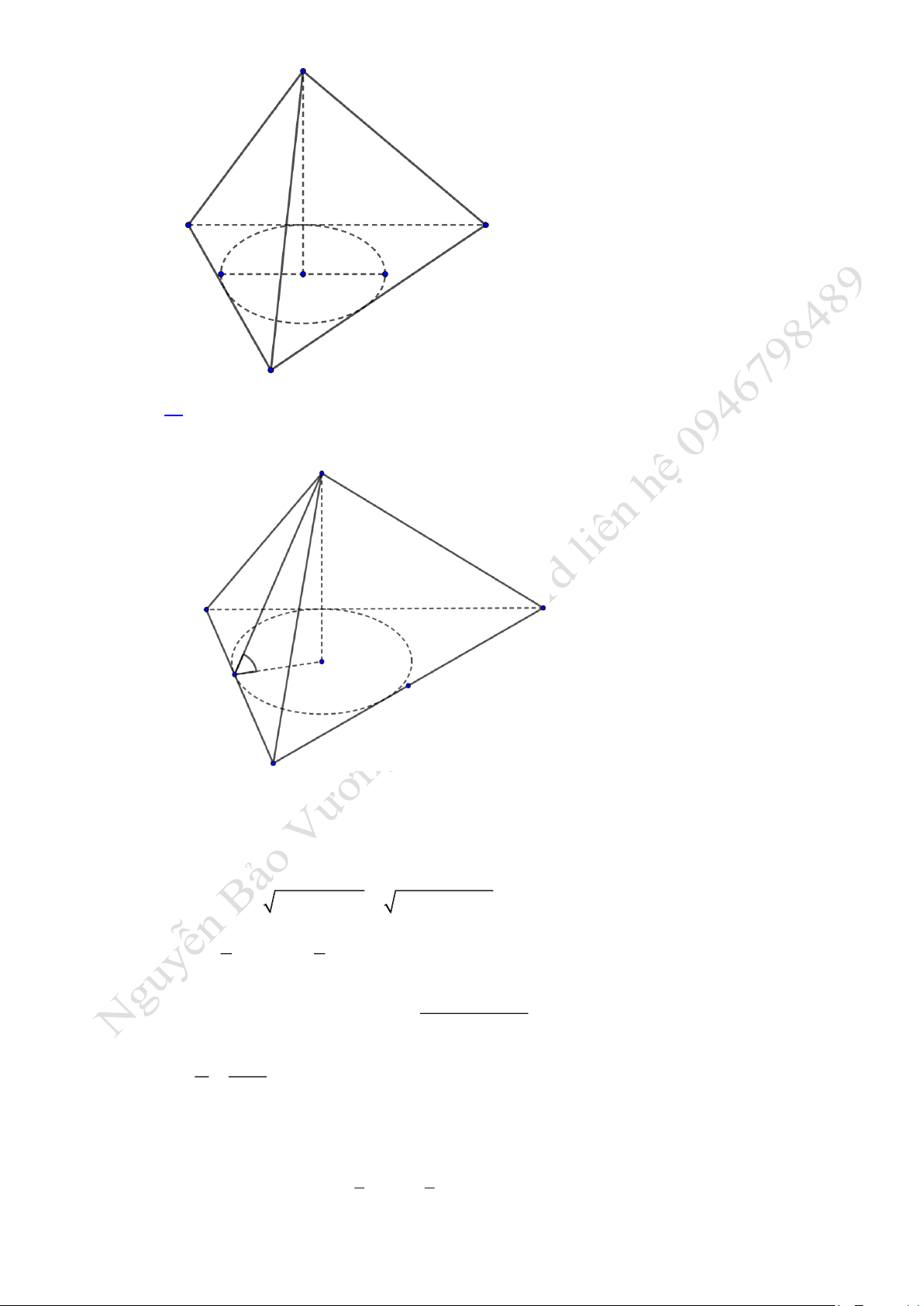
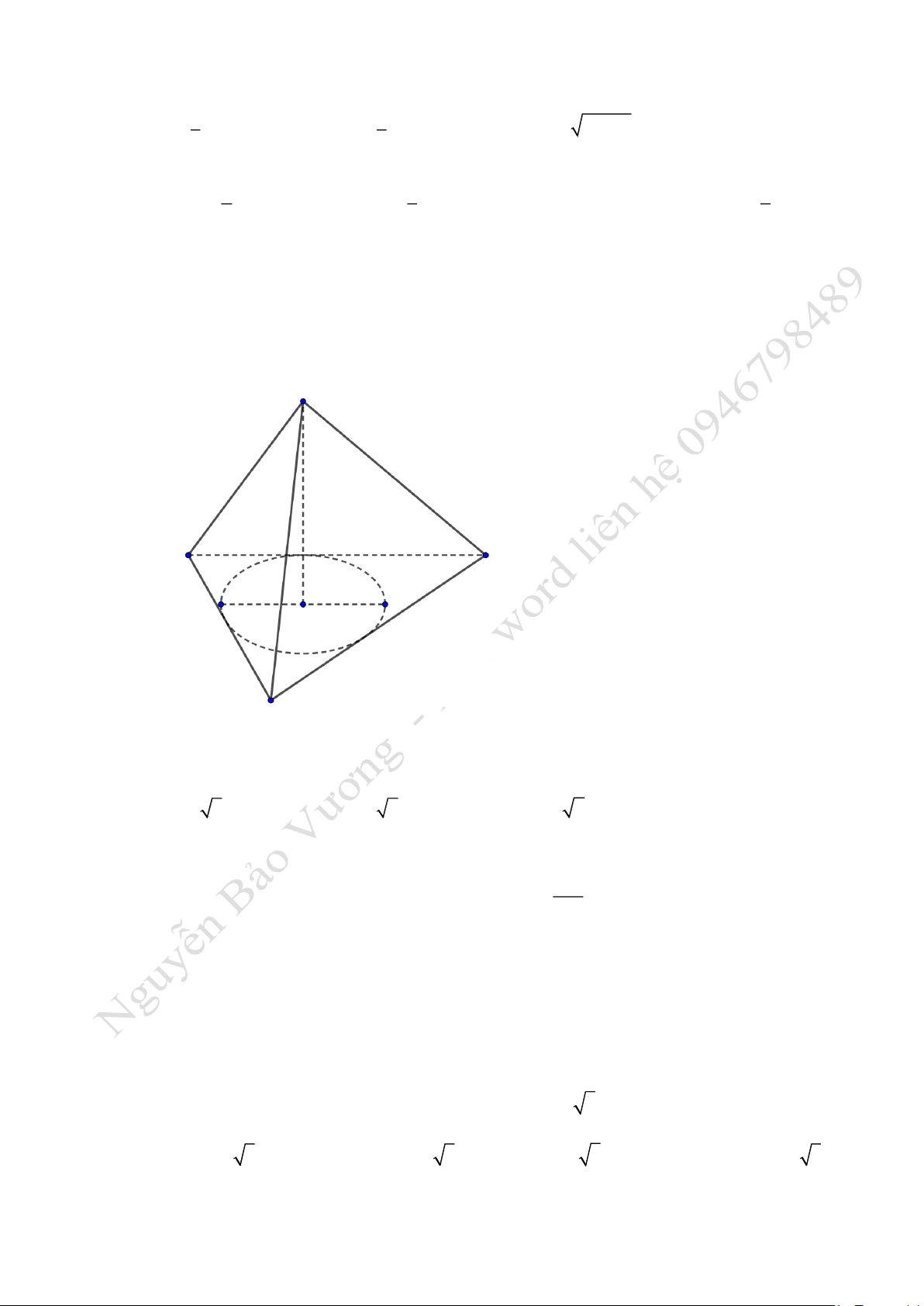
Câu 4. Cho hình nón đỉnh
S
, đáy là hình tròn nội tiếp tam giác
.ABC
Biết rằng
10 ,AB BC a==
12AC a=
, góc to bi hai mt phng
( )
SAB
và
( )
ABC
bằng
0
45
. Tính thể tích
V
của khối nón
đ cho.
A.
3
9.Va=
B.
3
12 .Va=
C.
3
27 .Va
=
D.
3
3.Va=
Câu 5. Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng
8.
Tính
chiều cao của hình nón này.
A.
23
. B.
6
. C.
22
. D.
6
.
Câu 6. Cho hình trụ có bán kính đáy bằng
1cm
. Một mt phng qua trục của hình trụ và cắt hình trụ
theo thiết diện là hình vuông. Tính thể tích của khối trụ đ cho.
A.
3
8 cm
. B.
3
2 cm
. C.
3
16 cm
3
. D.
3
16 cm
.
Câu 7. Cho hình trụ tròn xoay có độ dài đường sinh là
l
, độ dài đường cao là
h
và
r
là bán kính đáy.
Công thức diện tích xung qunh của hình trụ tròn xoay là
A.
Sxq =
p
rl
. B.
Sxq =
p
r2h
. C.
Sxq =
p
rh
. D.
Sxq =2
p
rh
.
Câu 8. Một hình trụ có bán kính đường tròn đáy
r=50cm
và có diện tích xung quanh bằng
5000
p
cm2
( )
thì chiều cao
h
của hình trụ là
A.
h=40cm
. B.
h=50cm
. C.
h=60cm
. D.
h=70cm
.
Câu 9. Hình trụ có bán kính đáy bằng
a
và chiều cao bằng
a3
. Khi đó diện tích toàn phần của hình
trụ bằng
A.
2
p
a23-1
( )
B.
p
a21+3
( )
C.
p
a23
D.
2
p
a21+3
( )
Câu 10. Cắt một khối trụ bi một mt phng qua trục của nó, ta được thiết diện là một hình vuông có
cnh bằng
3a
. Tính diện tích toàn phần
Stp
của khối trụ.
S
B
A
C
I