ĐỀ SỐ 8
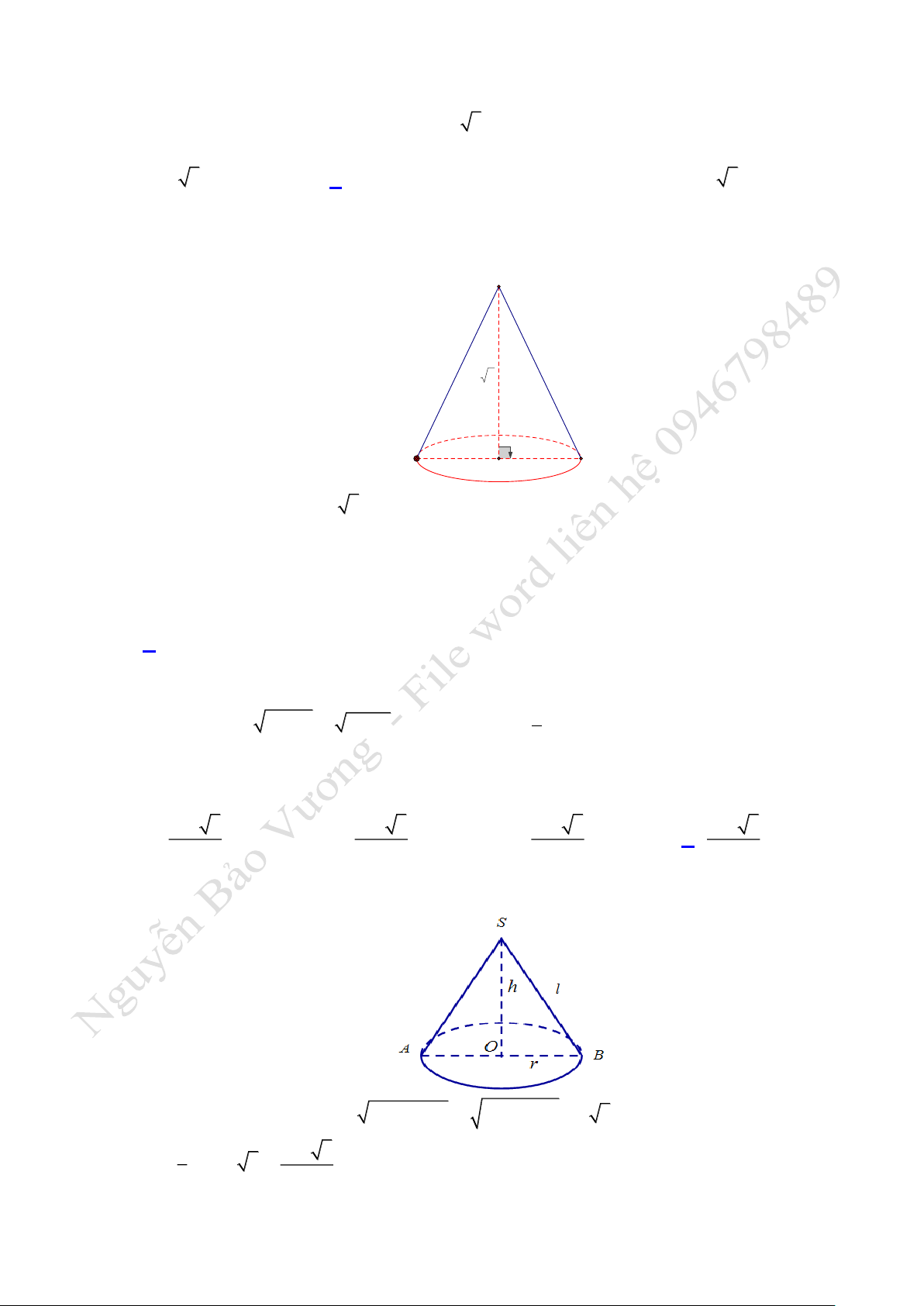
Câu 1. Cho hình nón tròn xoay có đường cao là
3a
, bán kính đáy là
a
. Tìm diện tích xung quanh
của hình nón đã cho.
A.
2
23a
. B.
2
2a
. C.
2
a
. D.
2
43a
.
Câu 2. Cho Hình nón
( )
N
có bán kính đáy bằng
3
và đường sinh bằng
5
. Tính thể tích
V
của khối
nón
( )
N
là
A.
12
. B.
20
. C.
36
. D.
60
.
Câu 3. Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài bằng
2a
. Thể tích của
khối nón là
A.
33
12
a
. B.
33
2
a
. C.
33
6
a
. D.
33
3
a
.
Câu 4. Thiết diện qua trục của một khối nón
( )
N
là một tam giác vuông cân và có cạnh góc vuông là
2a
. Tính thể tích
V
của khối nón
( )
N
.
A.
3
3
a
V
=
. B.
3
43a
V
=
. C.
3
23a
V
=
. D.
33
3
a
V
=
.
Câu 5. Cho tam giác
ABC
vuông tại
A
, có
30ABC =
và
AB a=
. Quay đường gấp khúc
BCA
quanh cạnh
AB
taọ thành hình nón tròn xoay. Tính diện tích xung quanh
xq
S
của hình nón đó.
A.
2
23
xq a
S
=
. B.
2
3
xq a
S
=
. C.
2
43
xq a
S
=
. D.
2
2
xq
Sa
=
.
Câu 6. Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7. Diện tích xung quanh của hình trụ đã
cho bằng
A.
175
3
. B.
175
. C.
70
. D.
35
.
Câu 7. Thể tích khối trụ có bán kính đáy bằng
a
, đường cao là
2a
là
A.
3
a
. B.
3
2a
. C.
3
3a
. D.
3
4a
.
Câu 8. Cho hình trụ có thiết diện qua trục là hình vuông cạnh
4a
. Diện tích xung quanh của hình trụ là
A.
2
8a
. B.
2
24 a
. C.
2
16 a
. D.
2
4a
.
Câu 9. Cho khối trụ có độ dài đường sinh gấp đôi bán kính đáy và thể tích bằng
16
. Diện tích xung
quanh của khối trụ đã cho bằng
A.
16
. B.
12
. C.
8
. D.
24
.
Câu 10. Cho hình chữ nhật
ABCD
có
2AB =
,
23AD =
và nằm trong mặt phẳng
( )
P
. Quay
( )
P
một vòng quanh đường thẳng
AD
. Khối tròn xoay được tạo thành có thể tích bằng
A.
43
. B.
8
. C.
83
. D.
16 3
.
Câu 11. Cắt mặt cầu
( )
S
bằng một mặt phẳng cách tâm một khoảng bằng
3cm
được thiết diện là hình
tròn có diện tích
2
16 cm
. Tính thể tích khối cầu đó
A.
3
250
3cm
B.
3
2500
3cm
C.
3
25
3cm
D.
3
500
3cm