ĐỀ SỐ 10
Câu 1. Cho hai số phức
112zi=+
và
223zi=−
. Phần ảo của số phức
12
32w z z=−
là?
A.
12i
. B.
12
. C.
11
. D.
11i
.
Câu 2. Cho số phức
. Tìm phần thực
a
và phần ảo
b
của
z
?
A.
a 1;b 2= = −
. B.
a 2;b 1= − =
. C.
a 1;b 0==
. D.
a 0;b 1==
.
Câu 3. Cho số phức
( )( )
2 1 1 3z i i i= + − + +
. Tính môđun của
z
.
A.
42
. B.
13
. C.
25
. D.
23
.
Câu 4. Cho hai số phức
12zi=+
và
253zi=−
. Số phức liên hợp của số phức
( )
12
32z z i z= − +
A.
z 13 4i= − −
. B.
z 13 4i= − +
. C.
z 13 4i=−
. D.
z 13 4i=+
.
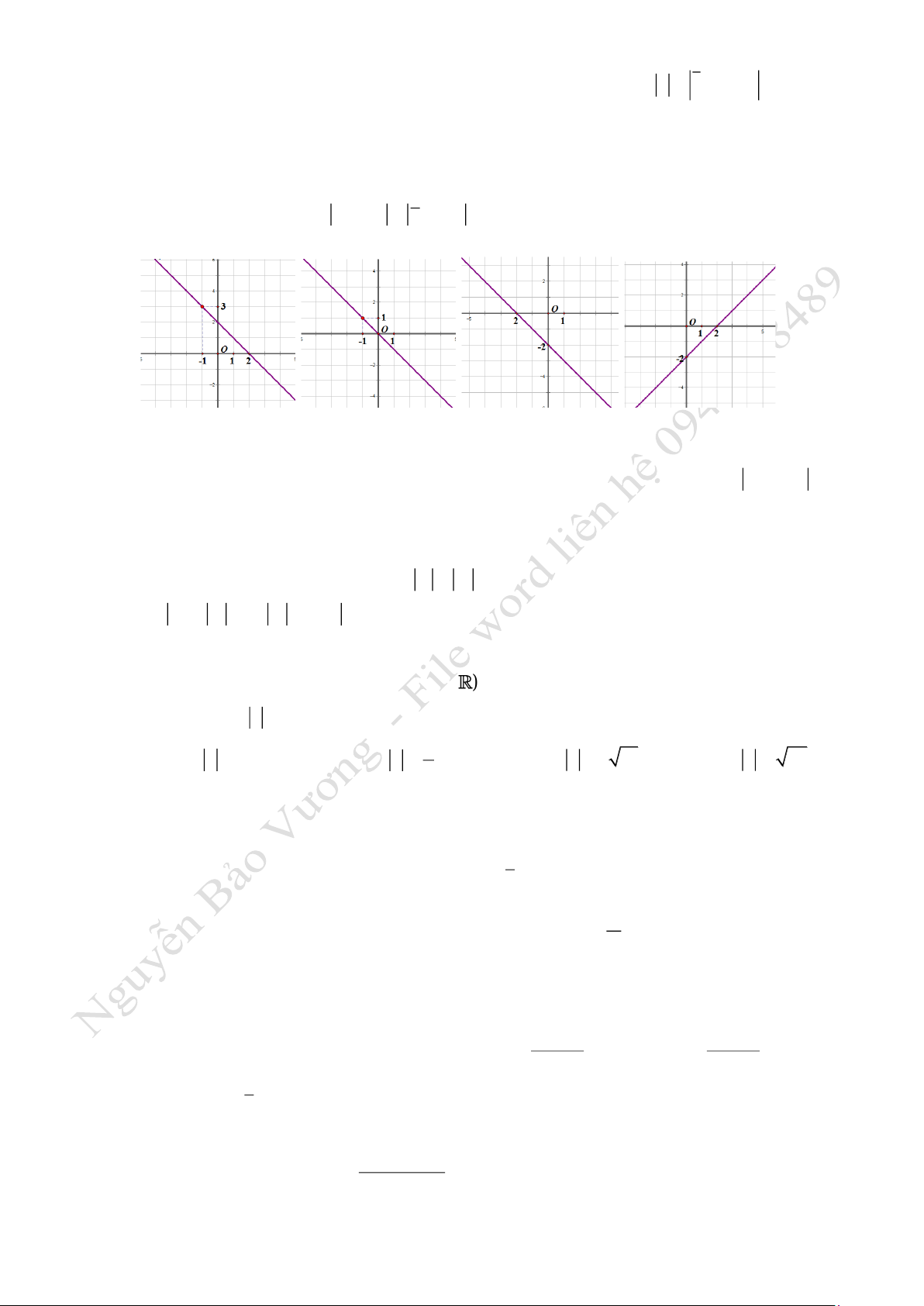
Câu 5. Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm
M
như hình bên ?
A.
z 1 2i=−
. B.
z 1 2i=+
. C.
z 2 i= − +
. D.
z 2 i=+
.
Câu 6. Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi=+
( )
, ; 0a b ab
.
M
là điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng ?
A.
M
đối xứng với
M
qua trục
Oy
.
B.
M
đối xứng với
M
qua trục
Ox
.
C.
M
đối xứng với
M
qua gốc tọa độ
O
.
D.
M
đối xứng với
M
qua trục đường thẳng
yx=
.
Câu 7. Phần thực, phần ảo của số phức
z
thỏa mãn
53
12
zi
i
=−
−
lần lượt là
A.
1; 1−
. B.
1; 2−
. C.
1;2
. D.
1;1
.
Câu 8. Cho số phức
z
thỏa mãn điều kiện
( )
1
25
1i
i z i
i
−
+ + = −
+
. Môđun của số phức
2
12w z z= + +
có
giá trị là? A.
10
B.
10−
. C.
100
D.
100−
.
Câu 9. Tính mô-đun số phức
( )( )
2
z 1 2i 2 i= − +
A.
5
. B.
55
. C.
55
. D.
55−
.
Câu 10. Tìm phần ảo của số phức
z
, biết
( ) ( )
1 1 3i z i i− = +
.
A.
3
. B.
3−
. C.
0
. D.
1−
.
Câu 11. Tập hợp các điểm
( )
;M x y
biểu diễn số phức
( )
,,z x yi x y R= +
:
34z z i= − +
là phương
trình một đường thẳng có dạng:
A.
6 8 25 0xy+−=
. B.
3 4 3 0xy+ − =
.
C.
6 8 25 0xy+ + =
. D.
6 8 25 0xy− + + =
.
Câu 12. Cho số phức z thỏa mãn
11z i z i− − = + −
, tập hợp các điểm
M
biểu diễn số phức z trên mặt
phẳng phức là hình:
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 13. Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức
z
thoả điều kiện
1 3 4zi+ −
.
A. Hình tròn tâm
( 1;3)I−
, bán kính
4r=
.B. Đường tròn tâm
( 1;3)I−
, bán kính
4r=
.
C. Hình tròn tâm
( 1; 3)I−−
, bán kính
4r=
.D. Đường tròn tâm
(1;3)I
, bán kính
4r=
.
Câu 14. Cho
12
, zz
là các số phức thoả mãn
12
1==zz
. Gọi
, Mm
lần lượt là giá trị lớn nhất và nhỏ
nhất của
1 2 1 2
1 1 1= + + + + +A z z z z
.Tính giá trị của
.mM
.
A.
18
B.
12
C.
6
D.
9
Câu 15. Cho số phức
,( 0, 0; , )z a bi a b a b= +
. Đặt
2
( ) 3f x ax bx= + +
. Biết
( )
(1) 0; 2 5ff
.
Tìm giá trị lớn nhất của
z
.
A.
max 3z=
B.
1
max 2
z=
C.
max 5 13z=
D.
max 65z=
Câu 16. Cho hai số phức
12
5 2 , 2 3z i z i= − = +
. Tìm số phức
12
z z z=+
A.
35zi=−
. B.
7zi=+
. C.
3zi= − +
. D.
75zi=−
.
Câu 17. Cho số phức
23zi= − +
. Tìm số phức
2w iz z=−
.
A.
4wi= − −
. B.
47wi= − −
. C.
87wi=−
. D.
8wi=−
.
Câu 18. Cho hai số phức
112zi=+
và
232zi=−
. Tìm số phức
1 2 2
w z z iz=+
.
A.
3 11wi= − +
. B.
97wi=+
. C.
9wi=−
. D.
1 11wi=+
.
Câu 19. Cho số phức
0z a bi= +
. Số phức
1
z−
có phần thực là
A.
ab+
. B.
ab−
. C.
22
a
ab+
. D.
22
b
ab
−
+
.
Câu 20. Cho số phức
13zi=−
. Số phức
2
z
có phần ảo là
A.
8−
. B.
6
. C.
6−
. D.
8
.
Câu 21. Tìm modun của số phức
23
(1 )(2 )
i
zii
−
=−+
A.
8
5
. B.
1
5
. C.
32
10
. D.
130
10
.
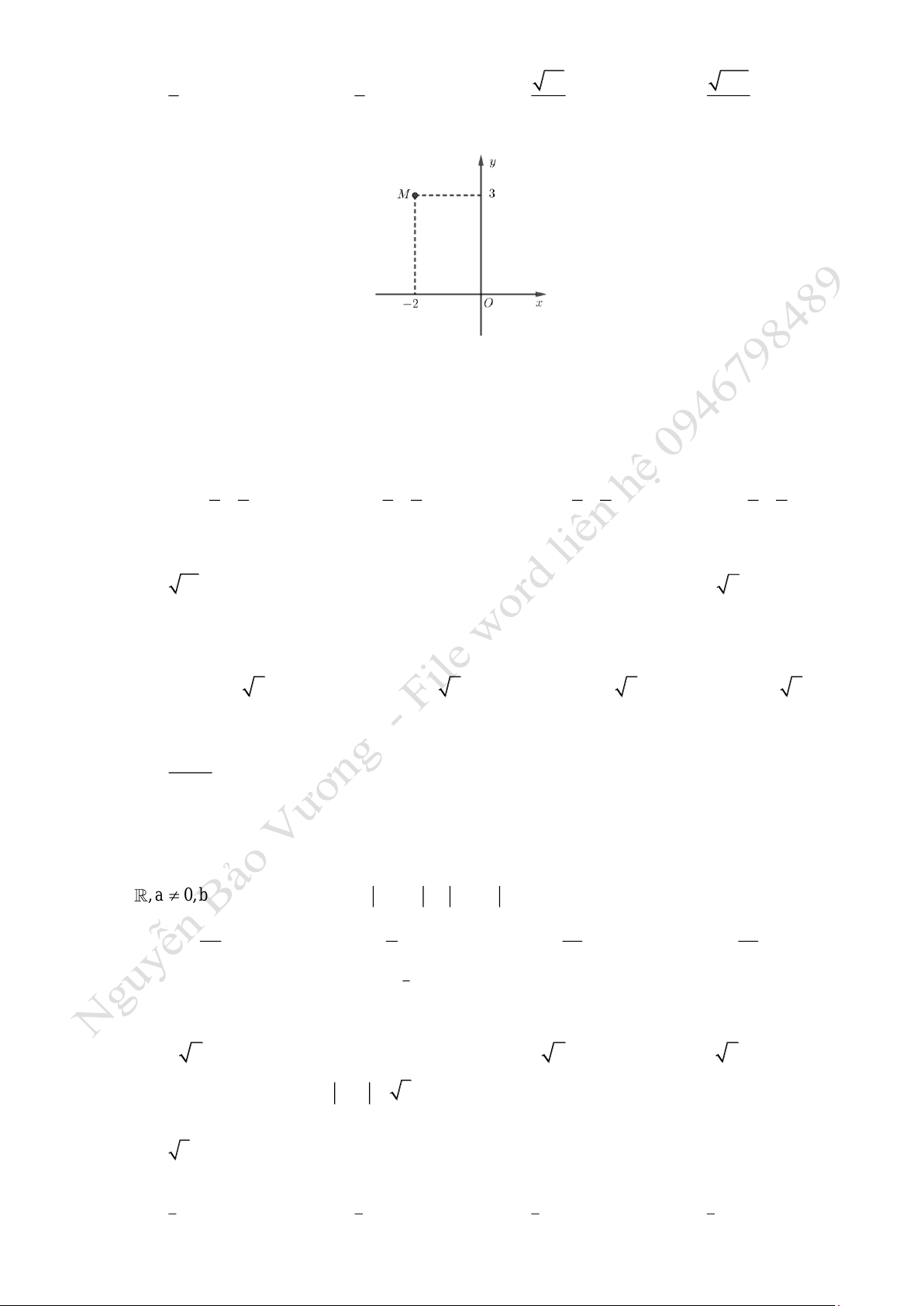
Câu 22. Trong mặt phẳng tọa độ, điểm
M
biểu diễn số phức nào sau đây ?
A.
32zi=−
. B.
23zi= − +
. C.
32zi=+
. D.
3zi=
.
Câu 23. Cho số phức
z
thỏa mãn
( )
4 2 8 6z i i i− − = −
. Phần thực của số phức
z
bằng
A.
12
. B.
4−
. C.
8−
. D.
8
.
Câu 24. Tìm số phức
z
thỏa mãn điều kiện
( )
3 5 3 0i z i− − + =
.
A.
92
55
zi= − +
. B.
92
55
zi=−
. C.
92
55
zi= − −
. D.
67
55
zi= − −
.
Câu 25. Cho số phức
z
thỏa mãn
( )
2 3 4 3 13 4i z i i+ + − = +
. Môđun của
z
bằng
A.
10
. B.
2
. C.
4
. D.
22
.
Câu 26. Cho
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 1 0z+=
(trong đó số phức
1
z
có phần ảo
âm). Tính
12
3zz+
.
A.
12
32z z i+=
. B.
12
32zz+ = −
. C.
12
32z z i+ = −
. D.
12
32zz+=
.
Câu 27. Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
22 5 0zz− + =
. Tìm tọa độ điểm biểu
diễn số phức
1
74i
z
−
trên mặt phẳng phức.
A.
( )
1; 2M
. B.
( )
1; 2N−
. C.
( )
3; 2P
. D.
( )
3; 2Q−
.
Câu 28. Gọi
1
z
,
2
z
là các nghiệm phức của phương trình
20az bz c+ + =
,
( )
2
, , , 0, 4 0a b c a b ac −
. Đặt
22
1 2 1 2
P z z z z= + + −
. Mệnh đề nào sau đây đúng?
A.
2
c
Pa
=
. B.
c
Pa
=
. C.
2c
Pa
=
. D.
4c
Pa
=
.
Câu 29. Cho số phức z thỏa mãn
( )
( )
3 1 3z i z i+ − + +
là một số thực. Biết rằng tập hợp các điểm biểu
diễn của
z
là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng
A.
42
B.
0
. C.
22
. D.
32
.
Câu 30. Xét số phức
z
thỏa mãn
15z+=
. Tập hợp các điểm biểu diễn số phức
( )
w 1 2 2 3i z i= − − +
là một đường tròn có bán kính bằng
A.
5
. B.
25
. C.
5
. D.
1
.
Câu 31. Tìm số phức liên hợp của số phức
( )( )
1 3 2 .z i i= − +
A.
1zi=+
. B.
5zi=+
. C.
5zi=−
. D.
1zi=−
.
Câu 32. Cho số phức
z
bất kỳ. Khẳng định nào sau đây là khẳng định sai?
A.
2
2=zz
B.
2
.=z z z
C.
=zz
D.
2
2=zz
Câu 33. Cho số phức
z
cóphần thực bằng
2
và phần ảo bằng
3−
. Modul của số phức
3iz+
là
A.
2 10
. B.
10
. C.
22
. D.
2
.
Câu 34. Ký hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4z 16 17 0z− + =
. Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
z
?
A.
1;2
2
M


B.
. C.
1
2; 2
M
−


D.
1
2; 2
M


Câu 35. Trong , phương trình
2
2 1 0xx+ + =
có nghiệm là
A.
( ) ( )
12
11
1 7 ; 1 7
44
x i x i= − − = − +
. B.
( ) ( )
12
11
1 7 ; 1 7
44
x i x i= + = −
.
C.
( ) ( )
12
11
1 7 ; 1 7
44
x i x i= − + = −
. D.
( ) ( )
12
11
1 7 ; 1 7
44
x i x i= + = − −
.
Câu 36. Phương trình nào dưới đây nhận hai số phức
12i+
và
12i−
là nghiệm?
A.
22 3 0zz+ + =
. B.
22 3 0zz− − =
.
C.
22 3 0zz− + =
. D.
22 3 0zz+ − =
.
Câu 37. Tìm tham số thực
m
để phương trình
( )
22 2 0z m z+ − + =
nhận số phức
1zi=−
làm một
nghiệm. A.
6m=
. B.
4m=
. C.
2m=−
. D.
2m=
.
Câu 38. Kí hiệu
1 2 3
, , z z z
và
4
z
là bốn nghiệm phức của phương trình
42
12 0.zz− − =
Tính tổng
1 2 3 4 .T z z z z= + + +
A.
4T=
. B.
23T=
. C.
4 2 3T=+
. D.
2 2 3T=+
.
Câu 39. Cho phương trình
20ax bx c+ + =
( )
0a
( )
1
. Hãy chọn khẳng định sai trong các khẳng định
sau. Biết rằng P là tích hai nghiệm, S là tổng hai nghiệm.
A. Nếu
0P
thì
( )
1
có
2
nghiệm trái dấu.
B. Nếu
0P
và
0S
thì
( )
1
có
2
nghiệm.
C. Nếu
0P
,
0S
và
0
thì
( )
1
có
2
nghiệm âm.
D. Nếu
0P
,
0S
và
0
thì
( )
1
có
2
nghiệm dương.
Câu 40. Cho phương trình
( )
2
0,5 2,7 1,5 0 1xx− + + =
. Hãy chọn khẳng định đúng trong các khẳng định
sau. A.
( )
1
có hai nghiệm trái dấu.
B.
( )
1
có hai nghiệm dương.
C.
( )
1
có hai nghiệm âm.
D.
( )
1
vô nghiệm.
Câu 41. Hai số
12−
và
12+
là các nghiệm của phương trình nào sau đây?
A.
2– 2 –1 0 xx=
. B.
22 –1 0xx+=
. C.
22 1 0xx+ + =
. D.
2– 2 1 0xx+=
.
Câu 42. Cho phương trình
20z bz c+ + =
có hai nghiệm
1
z
;
2
z
thỏa mãn
21
42z z i− = +
. Gọi
A
,
B
là
điểm biểu diễn các nghiệm của phương trình
22 4 0z bz c− + =
. Tính độ dài đoạn
AB
.
A.
85
. B.
25
. C.
45
. D.
5
.
Câu 43. Phương trình nào dưới đây nhận hai số phức và làm nghiệm?
A. . B. . C. . D. .
Câu 44. Gọi
12
,zz
là hai nghiệm phức của phương trình
2 2020
2 2 0zz+ + =
. Giá trị của
12
zz+
bằng
A.
2021
2
. B.
1011
2
. C.
2020
2
. D.
1010
2
.
Câu 45. Kí hiệu
1 2 3 4
; ; ;z z z z
là bốn nghiệm phức của phương trình
( )( ) ( )
2 2 2 2
3 6 3 3 9 02z z z z zzz −++ +− + + =
. Giá trị của biểu thức
1 2 3 4
z z z z+ + +
bằng
A.
( )
2 3 1 2+
. B.
2
. C.
( )
2 2 1 2+
. D.
( )
2 3 1 3+
.
LỜI GIẢI THAM KHẢO
Câu 1. Cho hai số phức
112zi=+
và
223zi=−
. Phần ảo của số phức
12
32w z z=−
là?
A.
12i
. B.
12
. C.
11
. D.
11i
.
Câu 2. Cho số phức
. Tìm phần thực
a
và phần ảo
b
của
z
?
A.
a 1;b 2= = −
. B.
a 2;b 1= − =
. C.
a 1;b 0==
. D.
a 0;b 1==
.
Câu 3. Cho số phức
( )( )
2 1 1 3z i i i= + − + +
. Tính môđun của
z
.
A.
42
. B.
13
. C.
25
. D.
23
.
Câu 4. Cho hai số phức
12zi=+
và
253zi=−
. Số phức liên hợp của số phức
( )
12
32z z i z= − +
A.
z 13 4i= − −
. B.
z 13 4i= − +
. C.
z 13 4i=−
. D.
z 13 4i=+
.
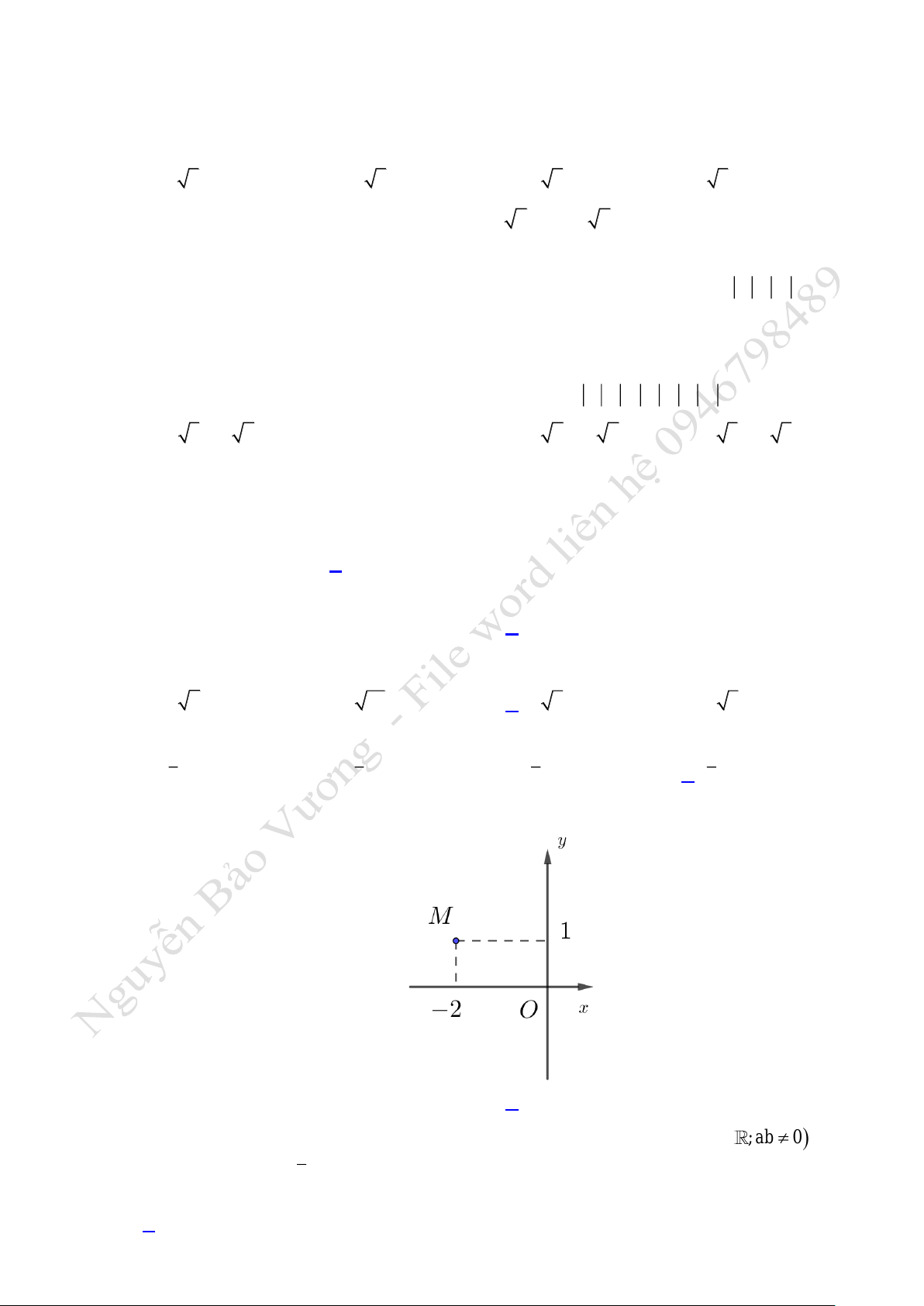
Câu 5. Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm
M
như hình bên ?
A.
z 1 2i=−
. B.
z 1 2i=+
. C.
z 2 i= − +
. D.
z 2 i=+
.
Câu 6. Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi=+
( )
, ; 0a b ab
.
M
là điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng ?
A.
M
đối xứng với
M
qua trục
Oy
.
B.
M
đối xứng với
M
qua trục
Ox
.
12i+
12i−
22 3 0zz+ + =
22 3 0zz− − =
22 3 0zz− + =
22 3 0zz+ − =