SỞ GD&ĐT NAM ĐỊNH
TRƯỜNG THCS YÊN
TIẾN
ĐỀ KIỂM TRA CHẤT LƯỢNG CUỐI HỌC KỲ II
NĂM HỌC 2020-2021
Môn: Toán 8 - Khối 8 - thời gian làm bài: 90 phút
Phần I- Trắc nghiệm(2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Phương trình
2
( 2)( 1) 0x x
− + =
có tập nghiệm là:
A.
{ }
1;2−
B.
{ }
2
C.
{ }
1;2
D.
{ }
1;1;2−
Câu 2. Điều kiện xác định của phương trình
2
2
1 1 1
x x
x x x
+ =
− + −
là :
A.
1x
B.
1x
−
C.
1x
−
hoặc
1x
D
1x
−
và
1x
Câu 3. Giá trị của biểu thức 3x – 2 không nhỏ hơn giá trị biểu thức 2x – 3 khi và chỉ khi:
A.
B.
1x
C.
1x
> −
D.
1x
>
Câu 4. Phương trình x -1 = m – 4 ( ẩn x) có nghiệm âm khi :
A.
5m
<
B.
4m
<
C.
3m
>
D.
3m
<
Câu 5. Tập nghiệm của bất phương trình
2
(1 ) 0x x− <
là
A.
0x
<
hoặc
1x
>
B.
0x
>
hoặc
1x
<
C.
1x
>
D.
1x<
Câu 6. Cho hình lăng trụ đứng tam giác có thể tích là 54 cm3, đáy là tam giác có độ dài ba cạnh là 3cm,
4cm, 5cm. Chiều cao của hình lăng trụ trên là :
A. 6 cm B. 9 cm C. 12 cm D. 15 cm
Câu 7. Bóng của một cột cờ trên mặt đất dài 45m ; ở cùng thời điểm đó một thanh sắt dài 2m có bóng
dài 3m> Chiều cao của cột cờ là :
A.20m B. 25m C. 30m D. 40m
Câu 8. Cho
ACB DMN∆ ∆:
. Biết
9.
ACB DMN
S S
∆ ∆
=
và AC = 2 cm. Độ dài cạnh DM bằng :
A. 6 cm B. 9 cm C. 12 cm D. 18 cm
Phần II - Tự luận (8,0 điểm)
Bài 1. ( 1,5 điểm) Cho biểu thức :
1 1 :
1 1
B x
x x
= +
− +
với
0; 1x x
a) Rút gọn biểu thức B.
b) Tính giá trị biểu thức B khi
3x
=
Bài 2: (2,5 điểm)
1) Giải bất phương trình sau và biểu diễn nghiệm trên trục số:
2 1
5
x+
-
2 2
3
x−
> -7
2) Giải phương trình sau:
3 1 2 10x x− − =
3) Tìm giá trị của m, biết rằng một trong hai phương trình sau đây nhận x = -1 làm nghiệm, phương
trình còn lại nhận x = 5 làm nghiệm:
2
(1 )( 1) 104x x− + = −
(1) và
2
(2 7)(8 mx) 0x+ − =
(2)
Bài 3: (3 điểm) Cho tam giác ABC vuông tại A, Đường cao AH.
a) Chứng minh
ABH CBA
∆ ∆
:
. Từ đó tính độ dài AB khi biết BH = 4cm; BC = 13cm.
b) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F.
Chứng minh AE . CH = AH . FC
c) Tìm vị trí của điểm E trên cạnh AB để tam giác EHF có diện tích nhỏ nhất
Bài 4: (1 điểm) Cho a, b, c >0 . Chứng minh rằng:
2 2 2
1 1 1a b c
b c a a b c
+ + + +
SỞ GD&ĐT NAM ĐỊNH
TRƯỜNG THCS YÊN
TIẾN
HDC KIỂM TRA CHẤT LƯỢNG CUỐI HỌC KỲ II
NĂM HỌC 2020-2021
Môn: Toán 8 - Khối 8 - thời gian làm bài: 90 phút
ĐÁP ÁN – BIỂU ĐIỂM
I Trắc nghiệm: (3 điểm) Mỗi câu đúng được 0.5 điểm
Câu 1 2 3 4 5 6 7 8
Đáp án B D A D C B C A
II. Tự luận ( 7 điểm)
Bài Nội dung trình bày Điểm
Bài 1
(1,5 đ)
a) với
0; 1x x
ta có
2
1 1 :
1 1
1 1 1
.
( 1)( 1) ( 1)( 1)
1 1 1
.
( 1)( 1)
2 1
.
( 1)( 1)
2 2
( 1)( 1) 1
B x
x x
x x
x x x x x
x x
x x x
x
x x x
x x x
= +
− +
+ −
= +
− + + −
+ + −
=
− +
=− +
= =
− + −
Vậy với
0; 1x x
thì
2
2
1
Bx
=−
0.25
0.25
0.25
0.25
a) Vậy với
0; 1x x
thì
2
2
1
Bx
=−
Ta có x = 3 thỏa mãn điều kiện xác định nên thay vào biểu thức B
ta có:
2
2 2 2 1
3 1 9 1 8 4
B= = = =
− −
Vậy x = 3 thì giá trị của biểu thức B bằng 1/4
0,25
0,25
0,25
Bài 2
(2.5 đ) 1) Ta có
2 1
5
x+
-
2 2
3
x−
> -7
(2 1).3 (2 2).5 7.15
5.3 3.5 15
6 3 10 10 105
15 15 15
6 3 10 10 105
6 10 105 3 10
4 118
4 : ( 4) 118: ( 4)
x
x x
x x
x x
x x
x
x
+ − −
− >
+ − −
− >
+ − + > −
− > − − −
− > −
− − < − −
<
Vậy nghiệm của bất phương trình trên là
Biểu diễn nghiệm trên trục số:
2)
3 1 2 10x x− − =
(1)
Ta có
3 1 3 1x x− = −
nếu
1
3 1 0 3
x x− ۳
3 1 (3 1)x x− = − −
nếu
1
3 1 0 3
x x− < <
+) Khi
13 1 0
3
x x −
khi đó
3 1 3 1x x− = −
Phương trình (1) trở thành: 3x – 1 – 2x = 10
10 1x
= +
11x
=
( Thỏa mãn ĐK)
x = 1 là nghiệm của phương trình (1)
+) Khi
13 1 0
3
x x< − <
khi đó
3 1 (3 1) 3 1x x x− = − − = − +
Phương trình (1) trở thành: - 3x + 1 – 2x = 10
9
5 10 1 5 9 5
x x x −
− = − − = =
( Thỏa mãn ĐK)
9
5
x−
=
là nghiệm của phương trình (1)
Vậy tập nghiệm của phương trình đã cho là:
9;1
5
S−
=
3) Ta thấy x = 5 là nghiệm của phương trình (1) vì khi thay x = 5
vào phương trình (1) ta được
2
(1 5)(5 1) 104
4.26 104
104 104
− + = −
− = −
− = −
luôn đúng
Vậy x = -1 là nghiệm của phương trình (2)
Thay x= -1 vào phương trình (2) ta được:
0.25
0.25
0.25
0.25
0,5
[ ]
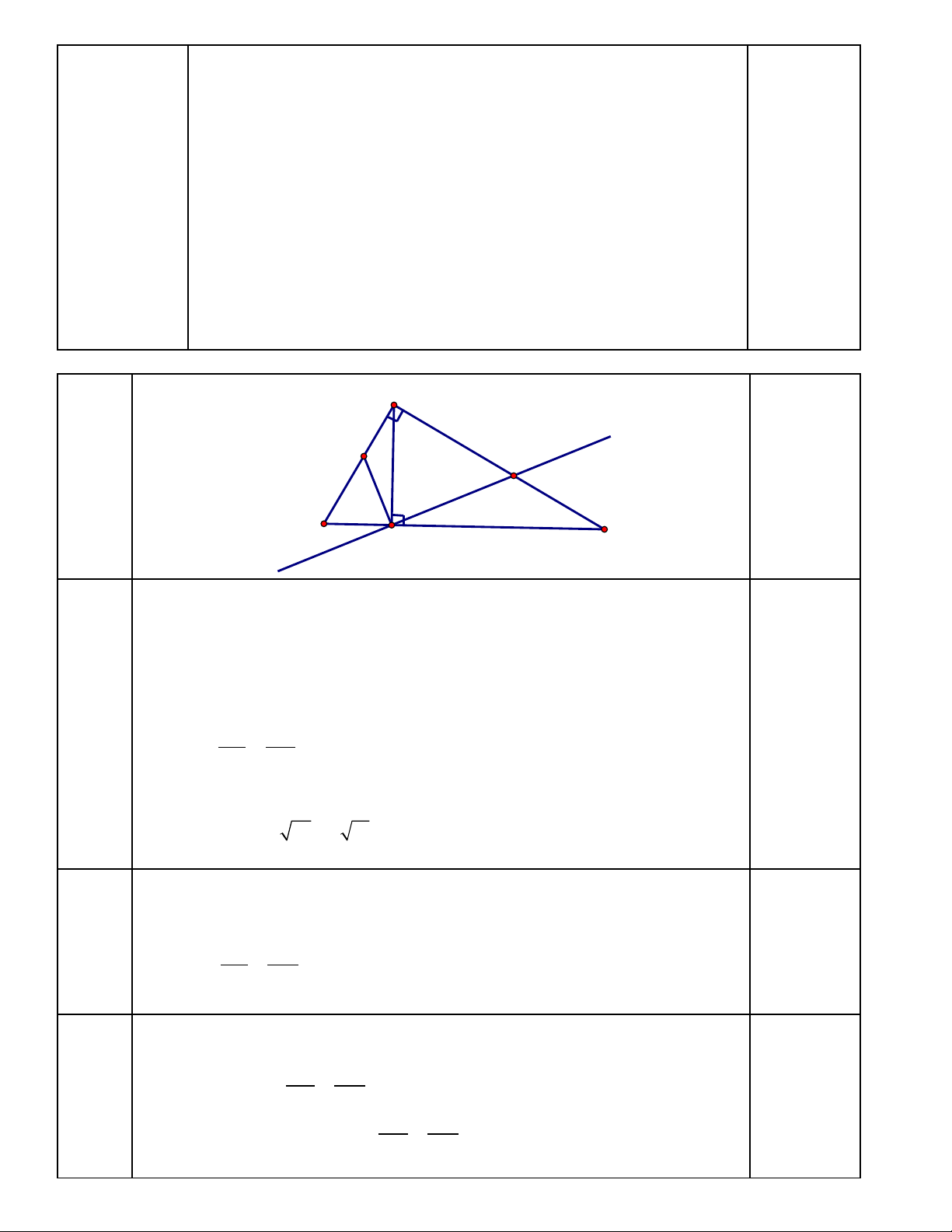
2
2( 1) 7 8 m( 1) 0
(2 7)(8 ) 0
8 0 8
m
m m
− + − − =
+ + =
+ = = −
Vậy m = -8 là giá trị cần tìm
Bài 3
(3đ)
F
H
A
B
C
E
Điểm
a)
1,25 đ a) +) Xét
ABH∆
vuông tại H và
CBA
∆
vuông tại A ta có
Góc B chung
ABH CBA
∆ ∆
:
( trường hợp đồng dạng của 2 tam giác
vuông)
+) Từ
ABH CBA∆ ∆:
2
.
AB BH AB BH BC
BC BA
= =
Thay số BH = 4cm; BC = 13cm.
Ta được AB2=4.13=52
52 2 13AB = =
0.5
0.25
0.5
b) 1 đ +) Ta có góc AHE = góc FHC ( vì cùng phụ với góc AHF)
+) Góc EAH = góc C vì cùng phụ với góc HAC
+)
( . )HAE HCF g g ∆ ∆:
AE AH
CF CH
=
(t/c)
AE . CH = AH . FC
0.25
0.25
0.25
0.25
c) 0,75
đ
B1: Cần chứng minh
EFABC H∆ ∆:
+) Chứng minh
CAH ABH
∆ ∆
:
( cùng đồng dạng với
CBA
∆
)
AC CH
AB AH
=
+)
EHA FHC
∆ ∆
:
suy ra
HF CH
HE AH
=
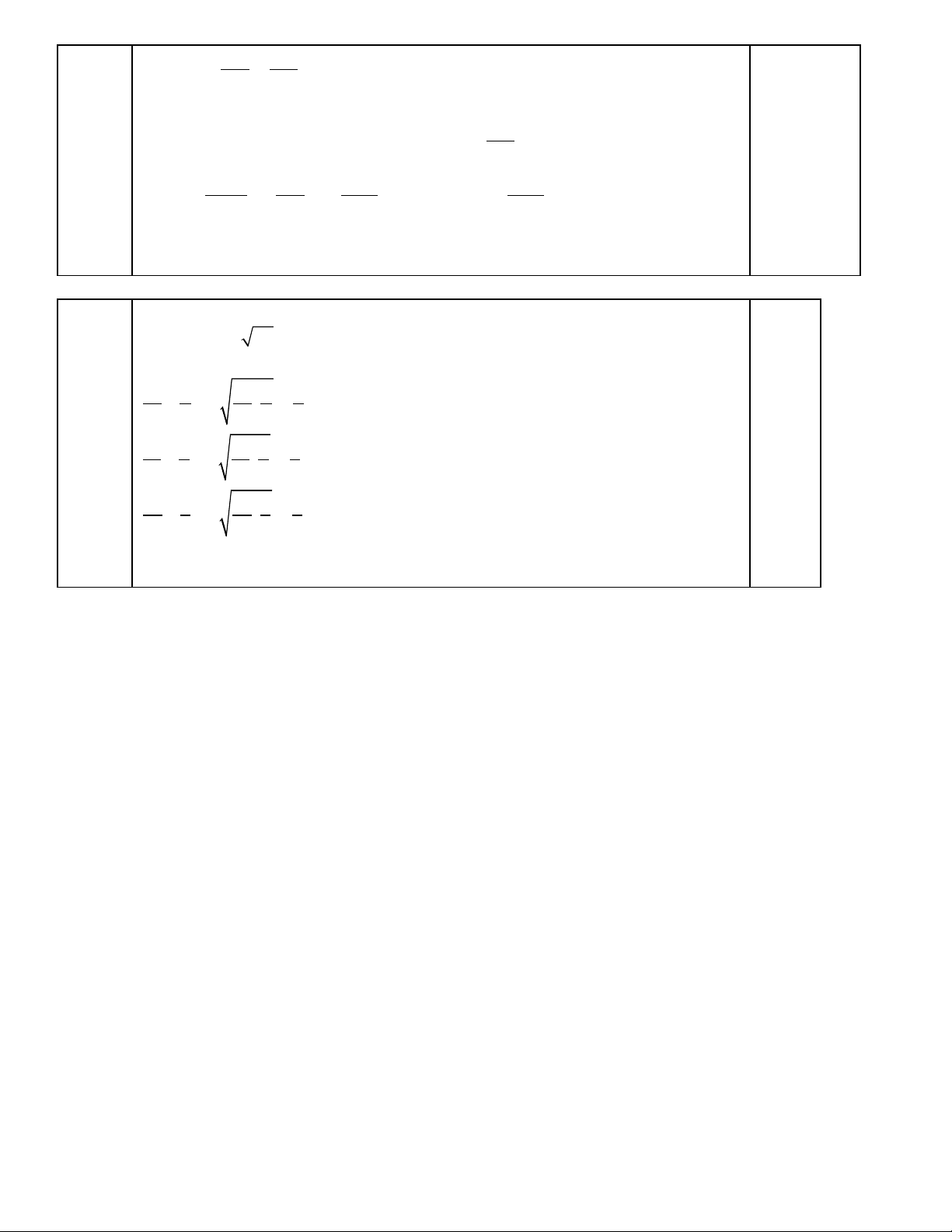
HF AC
HE AB
=
+)
EF H ABC
∆ ∆
:
với tỉ số đồng dạng
HE k
AB =
B2)
22 2
EF EF
2 2
.
HH ABC
ABC
S HE HE HE
S S
S AB AB AB
∆∆ ∆
∆
= = =
Mà
ABC
S
∆
và AB không đổi nên
EFH
S
∆
nhỏ nhất khi và chỉ khi HE nhỏ nhất
khi và chỉ khi
HE AB⊥
hay E là chân đường cao kẻ từ H tới AB
0,25
0,25
0,25
Bài 4
(1đ)
+) Học sinh chứng minh Bất đẳng thức cô si: với 2 số a, b không âm ta
có:
2a b ab+
+) Áp dụng ta có:
2 2
2 2
2 2
1 1 1
2 .
1 1 1
2 .
1 1 1
2 .
a a
b a b a b
b b
c b c b c
c c
a c a c c
+ =
+ =
+ =
Cộng vế với vế rồi rút gọn ta được điều phải chứng minh
0.25
0.5
0.25