KIỂM TRA CUỐI NĂM
MÔN TOÁN 8 – THỜI GIAN LÀM BÀI 90 PHÚT
Ma trận.
Nội dung
kiến thức
Mức độ nhận thức
CộngNhận biết Thông hiểu Vận dụng
thấp Vận dụng cao
TN TL TN TL TN TL TN TL
1. Giải
phương trình
.
Số câu:
Số điểm:
2
0.5
2
1.5
2.5
2. Biểu thức
hữu tỉ
Số câu:
Số điểm:
2
0.5
0.5
3. Bất
phương trình
Số câu:
Số điểm:
1
0.25
1
1
1.25
4. Giải BT
bằng cách
LPT
Số câu
Số điểm
1
2
2
5. Hình
không gian
Số câu
Số điểm
2
0.5
0.5
6. Tam giác
đồng dạng
Số câu
Số điểm
1
0.25
1
2.5
2.75
7. Tìm
GTNN
1
1
1
Tổng số câu:
Tổng số
điểm:
5
1.25
3
0.75
3
2.5
2
4.5
1
1
14
10
ĐỀ BÀI
I. Trắc nghiệm (2 điểm) Hãy viết chữ cái đứng trước đáp án đúng vào bài
làm.
Câu 1. Phương trình –x – m = x + 12 nhận x = -1 là nghiệm thì giá trị của m bằng:
A. m = -10 B. m = 11 C. m = 10 D. Giá trị khác
Câu 2. ĐKXĐ của phương trình
5
3 ( 2)( 3)
x x
x x x
=
− + −
là:
A. x -2 hoặc x 3 B. x -2 và x 3
C. x 3 hoặc x -2 D. x 0; x 3
Câu 3. Hình vẽ sau biểu diễn tập nghiệm của BPT nào?
5
0
A. x – 5 < 0 B. x + 5 < 0 C. –x + 5 0 D. x – 5 > 0
Câu 4. Trong các phương trình sau, phương trình nào là phương trình bậc nhất
một ẩn.
A. x – 1 = x + 2 B. (x – 1)(x – 2) = 0 C. ax + b =0 D. 2x +1 = 3x +5
Câu 5. Tập nghiệm của phương trình
2
( 1)( 2) 0
1
x x
x
− + =
−
(
1x
) là
A. S = {1; -2} B. S = {1} C. S = {-2} D. S =
Câu 6. Nếu ABC đồng dạng với A’B’C’ theo tỉ số đồng dạng là
2
5
và diện
tích ABC là 180cm2 thì diện tích A’B’C’ là
A. 80cm B. 120cm2 C. 2880cm2 D. 1125cm2
Câu 7. Cho hình hộp chữ nhật có các kích thước dài, rộng, cao lần lượt là 10cm,
8cm, 6cm. Thể tích của hình hộp chữ nhật đó là:
A. 960cm3 B. 480cm3 C. 240cm3 D. 120cm3
Câu 8. Cho hình lăng trụ đứng có đáy là tam giác vuông, biết hai cạnh góc vuông
của tam giác vuông là 3cm và 4m, chiều cao của hình lăng trụ là 9cm. Diện tích
xung quanh của hình lăng trụ đứng là
A. 24cm2 B. 36cm2 C. 63cm2 D. 108cm2
II. Tự luận (8 điểm)
Bài 1 (1,25 điểm)
Giải phương trình
a) 7 + 2x = 22 – 3x
b) |3x-6| = 5x+1
Bài 2 (0.75 điểm)
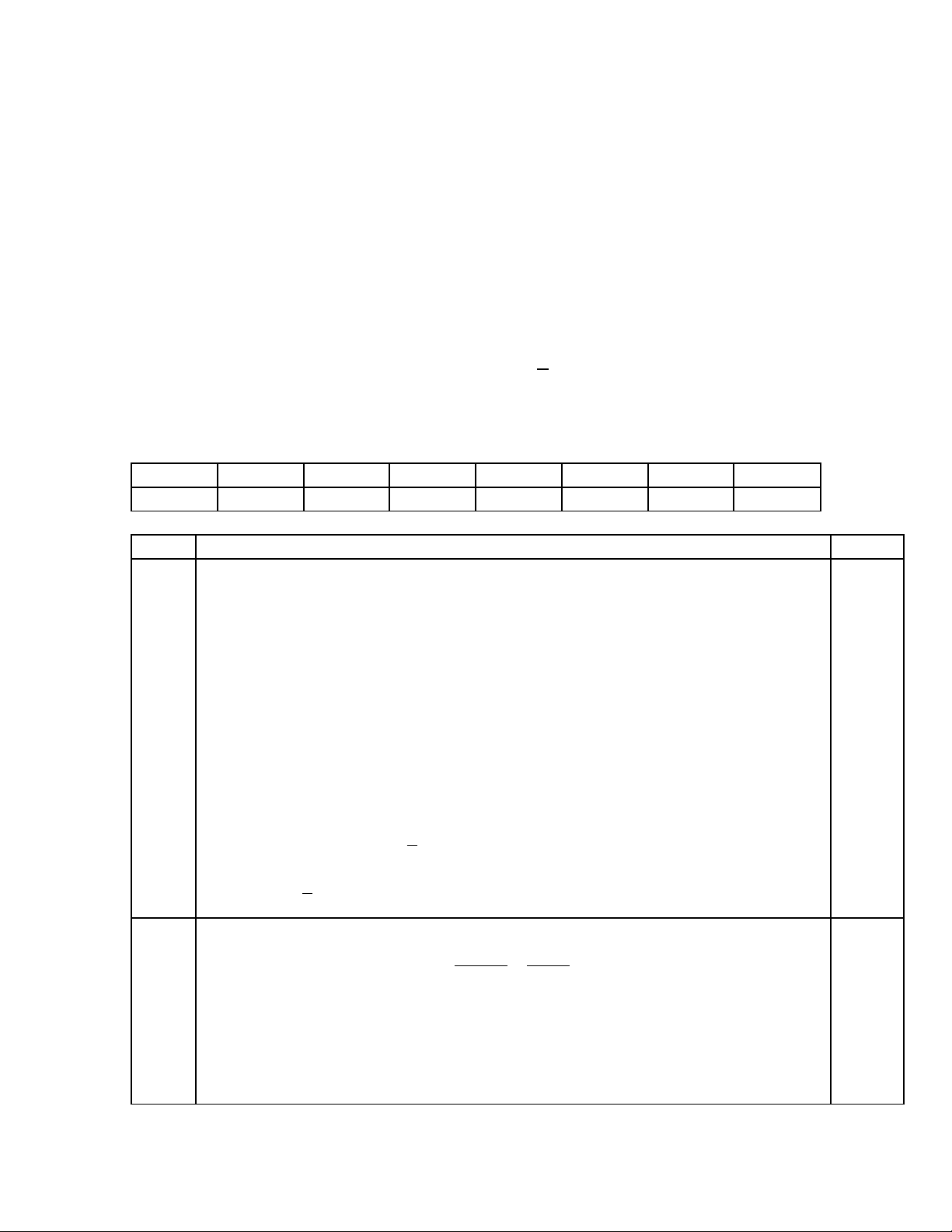
Giải BPT và biểu diễn tập nghiệm trên trục số.
10 3 6 1
2 3
x x− +
<
Bài 3 (2 điểm)
Một người đi xe máy từ A đến B với vận tốc 25 km/h. Lúc về người đó đi với vận
tốc 30km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB.
Bài 4 (3 điểm)
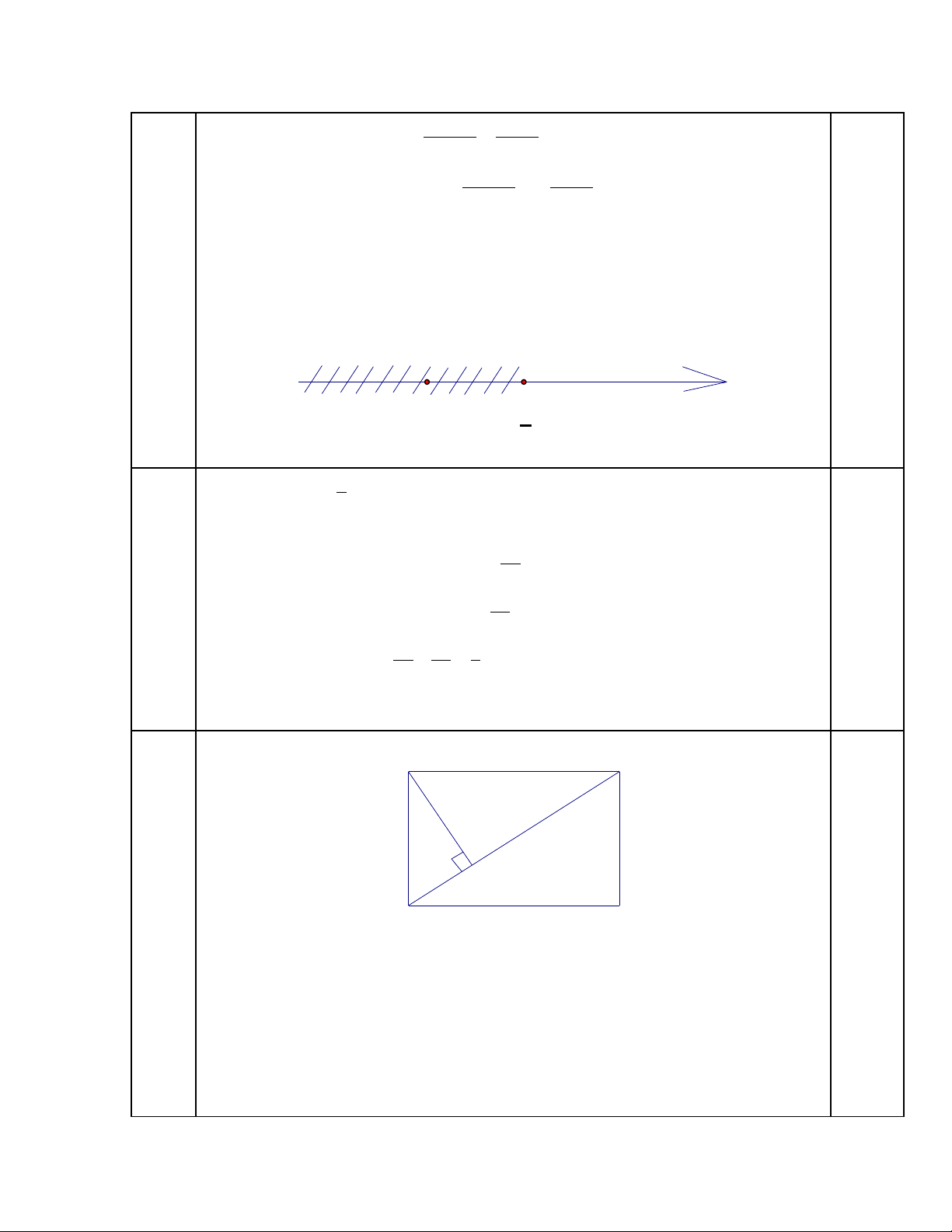
Cho hình chữ nhật ABCD có AB =8cm; BC = 6cm vẽ đường cao AH của tam giác
ADB.
a) Chứng minh tam giác AHB đồng dạng với tam giác BCD
b) Chứng minh AD2 = DH.DB
c) Tính DH; AH?
Bài 5 (1 điểm)
a) Tìm GTNN của A = 3y2 + x2 +2xy +2x +6y +3
b) Cho a + b = 1. Chứng minh rằng
3 3
1
2
a b ab+ +
Đáp án và biểu điểm
I. Trắc nghiệm. Mỗi câu đúng 0.25 điểm.
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8
A B C D C D B D
Câu Nội dung Điểm
1
(1,25
điểm)
a) 7 + 2x = 22 – 3x
2x + 3x = 22 – 7
5x = 15
x = 3
Kl nghiệm của phương trình x = 3
b) Giải phương trình |3x-6| = 5x+1
|3x-6| = 3x-6 nếu 3x-6 0 => x 2
|3x-6| = -3x+6 nếu 3x-6 < 0 => x < 2
Giải PT |3x-6| = 5x+1 với x 2
3x-6=5x+1-2x=7x=-3,5 (loại)
Giải PT |3x-6| = 5x+1 với x <2
-3x+6=5x+1-8x=-5x=
5
8
(thỏa mãn)
Kết luận x=
5
8
0.25
0.25
0.25
0.25
0.25
2
(0.75
điểm)
Giải BPT và biểu diễn tập nghiệm trên trục số.
10 3 6 1
2 3
x x− +
<
0.25
Kết luận x>4/3
(
4
3
0
0.25
0.25
3- Đổi 20 phút =
1
3
giờ
- Gọi độ dài quãng đường AB là x(km), x > 0
- Thời gian xe máy đi từ A đến B là
25
x
(giờ)
- Thời gian xe máy đi từ B về A là
30
x
(giờ)
- Theo bài ra ta có PT:
1
25 30 3
x x
− =
- Giải phương trình tìm được x = 50 (thỏa mãn điều kiện của ẩn)
- Kết luận độ dài quãng đường AB = 50(km)
0.25
0.25
0.25
0.25
0.25
0.5
0.25
4
H
D
C
B
A
a) Chứng minh tam giác AHB đồng dạng với tam giác BCD
- Xét tam giác AHB và tam giác BCD có:
Góc AHB = Góc BCD (=900)
Góc ABH = Góc BDC (so le trong, AB//CD)
Vậy tam giác AHB đồng dạng với tam giác BCD (g-g)
b) Chứng minh AD2 = DH.DB
- Xét tam giác AHD và tam giác BAD có:
0.25
0.25
0.25
0.25
Góc AHD = Góc BAD (=900)
Chung góc ADH
Vậy tam giác AHD đồng dạng với tam giác BAD (g-g)
Suy ra
AD HD
BD AD
=
suy ra AD2 = HD.DB
c) Tính DH; AH?
- Áp dụng định lí Py-ta-go vào tam giác ABD vuông tại A, tính được BD =
10 cm.
- Từ AD2 = HD.DB theo câu b, thay số suy ra HD = AD2:BD=36:10 =3,6
cm.
- Ta có tam giác AHB đồng dạng với tam giác BCD theo câu a.
Suy ra
AH AB
BC BD
=
(tỉ số đồng dạng)
Thay số suy ra AH = AB.BC : BD = 8.6 : 10 = 4,8 cm
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
5 a) Tìm GTNN của A =3y2 + x2 +2xy +2x +6y +3
2 2
2 2 2
2 2
2 2
3 2 2 6 3
( 2 ) (2 2 ) 1 (2 4 2)
[( ) 2( ) 1]+2(y 2 1)
( 1) 2( 1)
y x xy x y
x xy y x y y y
x y x y y
x y y
+ + + + +
= + + + + + + + +
= + + + + + +
= + + + +
Vì (x+y+1)2 0 với mọi x, y và (y+1)2 0 với mọi y
Nên
2 2
( 1) 2( 1) 0x y y+ + + +
Vậy A có GTNN là 0 khi y+1=0 => y= -1 và x -1 +1 =0 => x= 0
b)
3 3
3 3
2 2
2 2 2 2
2 2
2 2
2
1(1)
2
10
2
1
( )( ) 0
2
10 2 2 1 0
2
2 2(1 ) 1 0
2 2 4 2 1 0
1
4( ) 0
2
a b ab
a b ab
a b a ab b ab
a b a b
a a
a a a
a
+ +
+ + −
+ − + + −
+ − + −
+ − −
+ − + −
−
Dấu bằng sảy ra khi a = b = 1/2
0.25
0.25
0.25
0.25