S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KI M TRA CH T L NG H C KÌ IỂ Ấ ƯỢ Ọ
Đ NG THÁPỒNăm h c: 2012 – 2013ọ
Môn thi: TOÁN H CỌ – L p 11ớ
Th i gian: 90 phút (không k th i gian phát đ )ờ ể ờ ề
Ngày thi:
Đ Đ XU TỀ Ề Ấ
Tr ng THPT TP Cao Lãnhườ
A. Ph n chung (8 đi m).ầ ể
Câu I( 3 đi m)ể:
1). Tìm t p xác đ nh c a hàm s : y =ậ ị ủ ố
sin x
2sin x 1+
2). Gi i các ph ng trình sau: ả ươ
a). 2cos3x +
3
= 0.
b).
3
sin5x+2cos6x+ cos5x =0
Câu II( 2 đi m)ể:
a). Tìm s h ng ch a xố ạ ứ 4 trong khai tri n (2xể2 - 1 )5
b).M t l p có 40 h c sinh g m 22 nam và 18 n . Ch n m t nhóm g m 3ộ ớ ọ ồ ữ ọ ộ ồ
h c sinh. Tính xác su t đ 3 h c sinh đ c ch n đó có ít nh t 1 n .ọ ấ ể ọ ượ ọ ấ ữ
Câu III( 2 đi m)ể:
a).Trong m t ph ng t a đ Oxy cho đ ng th ng d có ph ng trình 2x+3y-5=0.ặ ẳ ọ ộ ườ ẳ ươ
Tìm nh c a d qua phép t nh ti n theo ả ủ ị ế
v
ur
=( 1;-2).
b).Cho tam giác ABC, d ng đi m M thu c c nh AB và đi m N thu c c nh ACự ể ộ ạ ể ộ ạ
sao cho MN song song v i BC và AM=2CNớ
Câu IV( 2 đi m)ể:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành .
Tìm giao tuy n c a hai m t ph ng (SAB) và (SCD).ế ủ ặ ẳ
B.Ph n riêng ( 2 đi m).ầ ể
Câu Va. ( 2 đi m)ể
1). Cho 1;x+1;y-1;19 là các s h ng liên ti p c a m t c p s c ng. Tìm x; yố ạ ế ủ ộ ấ ố ộ
2). Cho t p h p A={0, 1, 2, 3, 4, 5, 6 }. T t p A có th l p đ c bao nhiêu sậ ợ ừ ậ ể ậ ượ ố
t nhiên l có ba ch s khác nhau ?ự ẻ ữ ố
Câu Vb. ( 2 đi m)ể
1). Cho t p h p A={0, 1, 2, 3, 4, 5, 6 }. T t p A có th l p đ c bao nhiêu sậ ợ ừ ậ ể ậ ượ ố
t nhiên có ba ch s khác nhau ?ự ữ ố
2). Tìm giá tr l n nh t và nh nh t c a hàm s : y= ị ớ ấ ỏ ấ ủ ố
2sin x 3cosx 1
sin x cosx 2
+ -
- +
ĐÁP ÁN
CÂU ĐÁP ÁN ĐIỂ
M
I1). Tìm t p xác đ nh c a hàm s : y =ậ ị ủ ố
sin x
2sin x 1+
1. đ
Đi u ki n xác đ nh 2sinx+1≠0ề ệ ị 0.25
2sinx+1≠0
ￛ
sinx
π
x k2π
16
7π
2x k2π
6
ￛ-
ￛ
ￛￛ +
ￛ
-ￛ
ￛ
ￛ ￛ ￛ
ￛ
ￛￛ +
ￛ
ￛ
ￛ
ￛ
0.25
0.25
K t lu n T p xác đ nh D=R\{ế ậ ậ ị
π 7π
k2π; k2π k Z
6 6
-+ + ￛ
}0.25
2).Gi i các ph ng trình sau: ả ươ 2. đ
a). 2cos3x +
3
= 0
0.25
5π
3x k2π
6
= +� �
0.25
5π 2
x kπ
18 3
= +� �
0.5
b).
3
sin5x+2cos6x+ cos5x =0
ￛ
3 1
sin 5x cos5x cos 6x
2 2
+ = -
0.25
π
cos(5x ) cos(6xπ)
3
- = +�
0.25
π
6xπ 5x k2π
3
π
6xπ (5x ) k2π
3
ￛ
ￛ+ = - +
ￛ
ￛￛ
ￛ+ = - - +
ￛ
ￛ
ￛ
ￛ
0.25
4π
x k2π
3
2π 2
x kπ
33 11
ￛ
ￛ= - +
ￛ
ￛￛ
ￛ= - +
ￛ
ￛ
ￛ
0.25
IIa a). Tìm s h ng ch a xố ạ ứ 4 trong khai tri n (2xể2 - 1 )5 1. đ
Trong khai tri n nh th c (2xể ị ứ 2 -1)5 s h ng ch a xố ạ ứ 4 là
3 2 2 3 4
5
C (2x ) ( 1) 40x- = -
0.5
+0.5
IIb 1 đ
S cách ch n 3 h c sinh trong 40 h c sinh là ố ọ ọ ọ
3
40
C
= 9880 0.25
G i A là bi n c trong 3 h c sinh đ c ch n có ít nh t m t nọ ế ố ọ ượ ọ ấ ộ ữ
A
là bi n c trong 3 h c sinh đ c ch n c 3 là nam.ế ố ọ ượ ọ ả
Ta có
3
22
A
Ω C=
=1540 0.25
V y xác su t c n tính là P(A)=1-ậ ấ ầ
P(A)
=1-
3
22
3
40
C 1540 8340
1
C 9880 9880
= - =
=
417
494
0.5
IIIa 1 đ
Phép t nh ti n theo ị ế
v
ur
=( 1;-2), bi n M(x;y) thành Mế/(x/;y/) theo bi uể
th c t a đ ứ ọ ộ
x x 1 x x 1
y y 2 y y 2
� �
ￛ ￛ
- = = -
� �
� �
ￛ
� �
� �
ￛ ￛ
- = - = +
� �
� �
0.25
Ph ng trình dươ / là nh c a d qua phép t nh ti n là:ả ủ ị ế
2(x/-1)+3(y/+2)-5=0
2x 3y 1 0
ￛ ￛ
+ - =�
0.25
0.25
V y ph ng trình dậ ươ / là:2x+3y-1=0. 0.25
IIIb. 1 đ
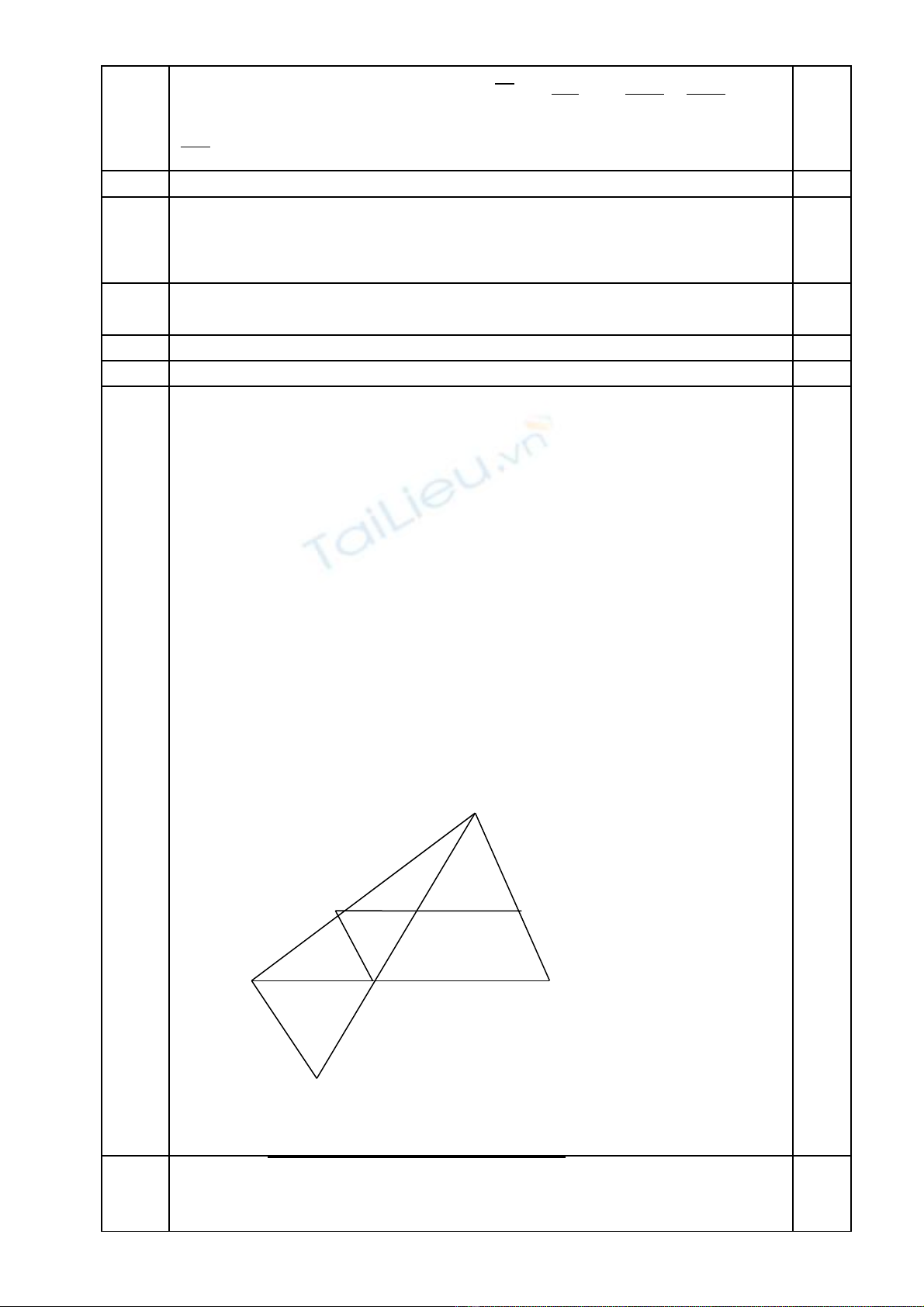
Gi s đã d ng đ c hai đi m M, N th a đ bài . Khi đó t M vả ử ự ượ ể ỏ ề ừ ẽ
đ ng th ng song song v i AC c t BC t i D thì tam giác AMD cóườ ẳ ớ ắ ạ
AM=2MD và góc AMD bù v i góc A c a tam giác ABC.ớ ủ
Cách d ng:ự
+D ng tam giác ABK có AB=2BK và góc ABK bù v i góc A c aự ớ ủ
tam giác ABC ( tia BK// tia AC). G i D là giao đi m c a AK v iọ ể ủ ớ
BC.
+D ng DM//AC ( M thu c AB). ự ộ
+D ng N là nh c a M qua phép t nh ti n véct ự ả ủ ị ế ơ
DC
uuur
.
Ch ng minh theo cách d ng ta th y ngay và bài tóan có m tứ ự ấ ộ
nghi m khi AC c t BC t i D thu c c nh BC . ệ ắ ạ ộ ạ
A
M N
B C
D
K
0.25
0.5
0.25
IV Ta có AB//CD và AB không thu c mp(SCD) nên AB//mp(SCD).ộ
Ta có mp(SAB) và mp(SCD) có đi m S chung,ể
nên giao tuy n c a hai m t ph ng c n tìm là đ ng th ng qua Sế ủ ặ ẳ ầ ườ ẳ
0.25
0.25
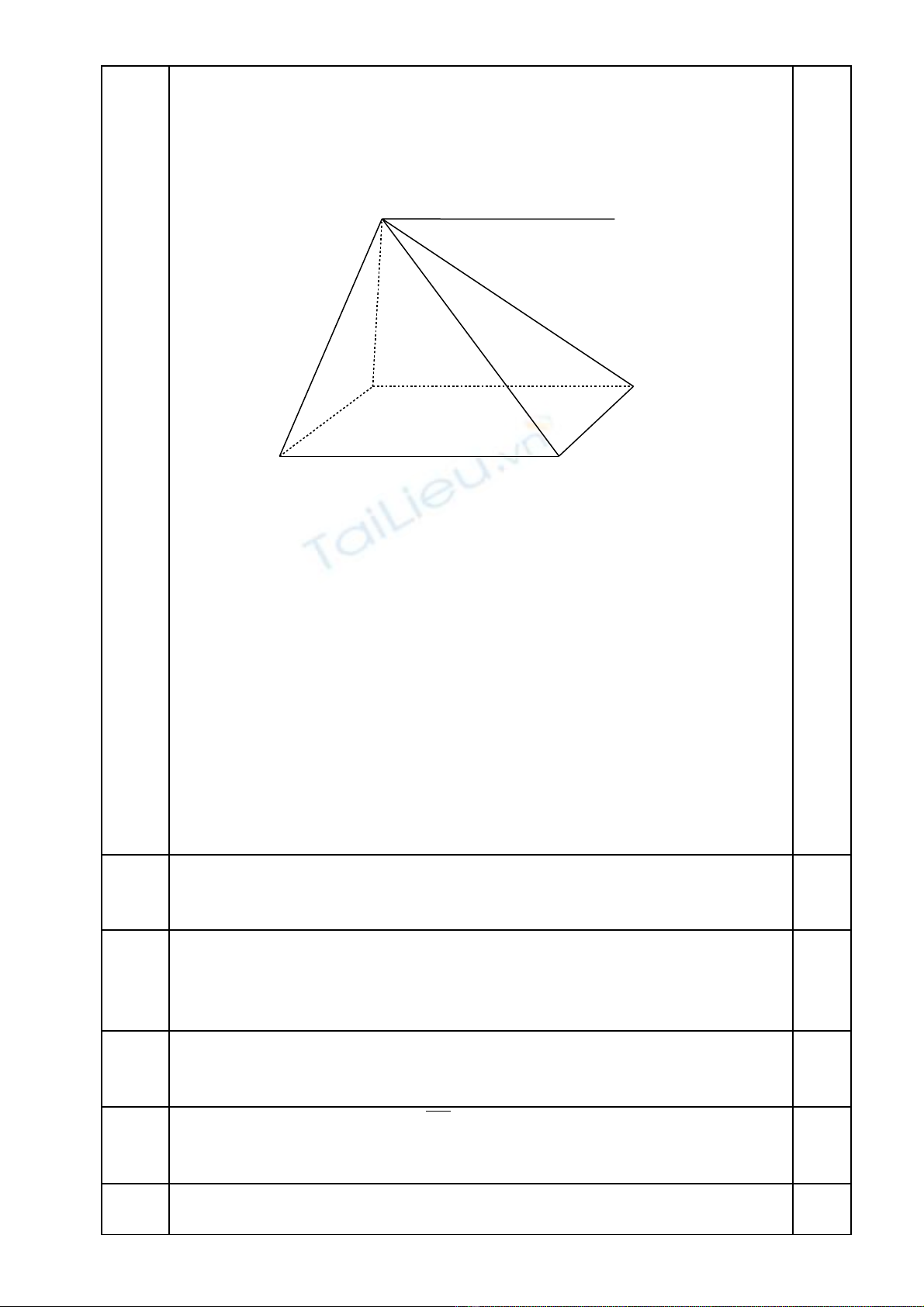
và song song v i CDớ
S X
D C
A B
0.5
Va 1). Cho 1;x+1;y-1;19 là các s h ng liên ti p c a m t c p s c ng.ố ạ ế ủ ộ ấ ố ộ
Tìm x; y
1 đ
Không m t tính ch t t ng quát g i các s h ng c a c p s c ngấ ấ ổ ọ ố ạ ủ ấ ố ộ
đó là u1,u2,u3,u4, có công sai là d.
Khi đó u4-u1=19-1=18=3d
ￛ
d=6
D th y x=6, y-1=7+6=13 nên y=14ễ ấ 0.5
0.5
2). Cho t p h p A={0, 1, 2, 3, 4, 5, 6 }. T t p A có th l p đ cậ ợ ừ ậ ể ậ ượ
bao nhiêu s t nhiên l có ba ch s khác nhau ?ố ự ẻ ữ ố 1 đ
G i s l có 3 ch s là x=ọ ố ẻ ữ ố
abc
; c có 3 cách ch n ọ
a≠c, ≠0 nên a có 5 cách ch n, b có 5 cách ch n ( b≠a,≠c)ọ ọ
V y có 3.5.5=75 s . ậ ố
0.25
0.5
0.25
Vb 1). Cho t p h p A={0, 1, 2, 3, 4, 5, 6 }. T t p A có th l p đ cậ ợ ừ ậ ể ậ ượ
bao nhiêu s t nhiên có ba ch s khác nhau ?ố ự ữ ố 1 đ
G i s có 3 ch s là x=ọ ố ữ ố
abc
; a có 6 cách ch n a≠0 ọ
b có 6 cách ch n ( b≠a), c≠a,c ≠b nên c có 5 cách ch n,ọ ọ
V y có 6.6.5=180 s . ậ ố
0.25
0.5
0.25
2)Tìm giá tr l n nh t và nh nh t c a hàm s : y=ị ớ ấ ỏ ấ ủ ố
2sin x 3cos x 1
sin x cosx 2
+ -
- +
1 đ
Vì sinx-cosx=
π
2 sin(x )
4
-
nên sinx-cosx+2≠0 v i m i x là s th cớ ọ ố ự
y=
2sin x 3cos x 1
sin x cosx 2
+ -
- +
ￛ
(y-2)sinx-(y+3)cosx=-(2y+1) đ ph ngể ươ
trình có nghi m theo x ệ
2 2 2
(y 2) (y 3) (2y 1)- + + +� �
2
y y 6 0 3 y 2+ - -� � � � �
V y giá tr nh nh t c a y là -3 khi x=ậ ị ỏ ấ ủ
π
2
-
V y giá tr l n nh t c a y là 2 khi x=0ậ ị ớ ấ ủ
0.25
0.25
0.25
0.25
0.25