ĐỀ ÔN TẬP SỐ 1 THI ĐẠI HỌC, CAO ĐẲNG
Môn thi: TOÁN, khối A
Thời gian làm bài 180 phút, không kể thời gian phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I (2 điểm)Cho hàm số
113 23 xmmxxy (1), m là tham số thực.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = -1.
2. Tìm các giá trị của m để tiếp tuyến của đồ thị hàm số (1) tại điểm có hoành độ x = -1 đi
qua điểm A(1;2)
Câu II (2 điểm) 1. Giải phương trình tgx = cotgx + 4cos2 2x.
2. Giải phương trình 12 x + x23=
2
)12( 2
x (x
R).
Câu III (2 điểm) Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng:
d1:
1
3
2
3
2
3
zyx và d 2:
.0766
013665
zyx
zyx
1. Chứng minh rằng d1 và d2 cắt nhau.
2. Gọi I là giao điểm của d1 và d 2. Tìm tọa độ các điểm A,B lần lượt thuộc d1, d2 sao cho
tam giác IAB cân tại I và có diện tích bằng
42
41 .
Câu IV (2 điểm) 1.Tính tích phân I =
3
2
13.
22x
xdx
2. Giải phương trình )
4
sin(
x
e=tgx.
PHẦN RIÊNG Thí sinh chỉ được làm 1 trong 2 câu: V.a hoặc V.b
Câu V.a. Theo chương trình KHÔNG phân ban (2 điểm)
1. Cho tập hợp E =
.7,5,4,3,2,1,0 Hỏi có bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác
nhau được lập từ các chữ số của E?
2. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC các đường cao kẻ từ đỉnh B và
đường phân giác trong của góc A lần lượt có phương trình là 3x + 4y + 10=0 và x - y +
1=0; điểm M(0;2) thuộc đường thẳng AB đồng thời cách điểm C một khoảng bằng 2.
Tìm tọa độ các đỉnh cuả tam giác ABC.
Câu V.b. Theo chương trình phân ban (2 điểm)
1. Giải bất phương trình log
3
1.0
1
32
log2
x
x
2. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại đỉnh B, BA = BC = 2a, hình
chiếu vuông góc của S trên mặt phẳng đáy (ABC) là trung điểm E của AB và SE = 2a.
Gọi I, J lần lượt là trung điểm của EC, SC; M là điểm di động trên tia đối của tia BA sao
cho góc E MC
ˆ
=
(
<900) và H là hình chiếu vuông góc của S trên MC. Tính thể tích
của khối tứ diện EHIJ theo a,
và tìm
để thể tích đó lớn nhất.
ĐÁP ÁN – THANG ĐIỂM
Môn thi: TOÁN, khối A
Câu Nội dung Điểm
I 2,00
1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1,00 điểm)
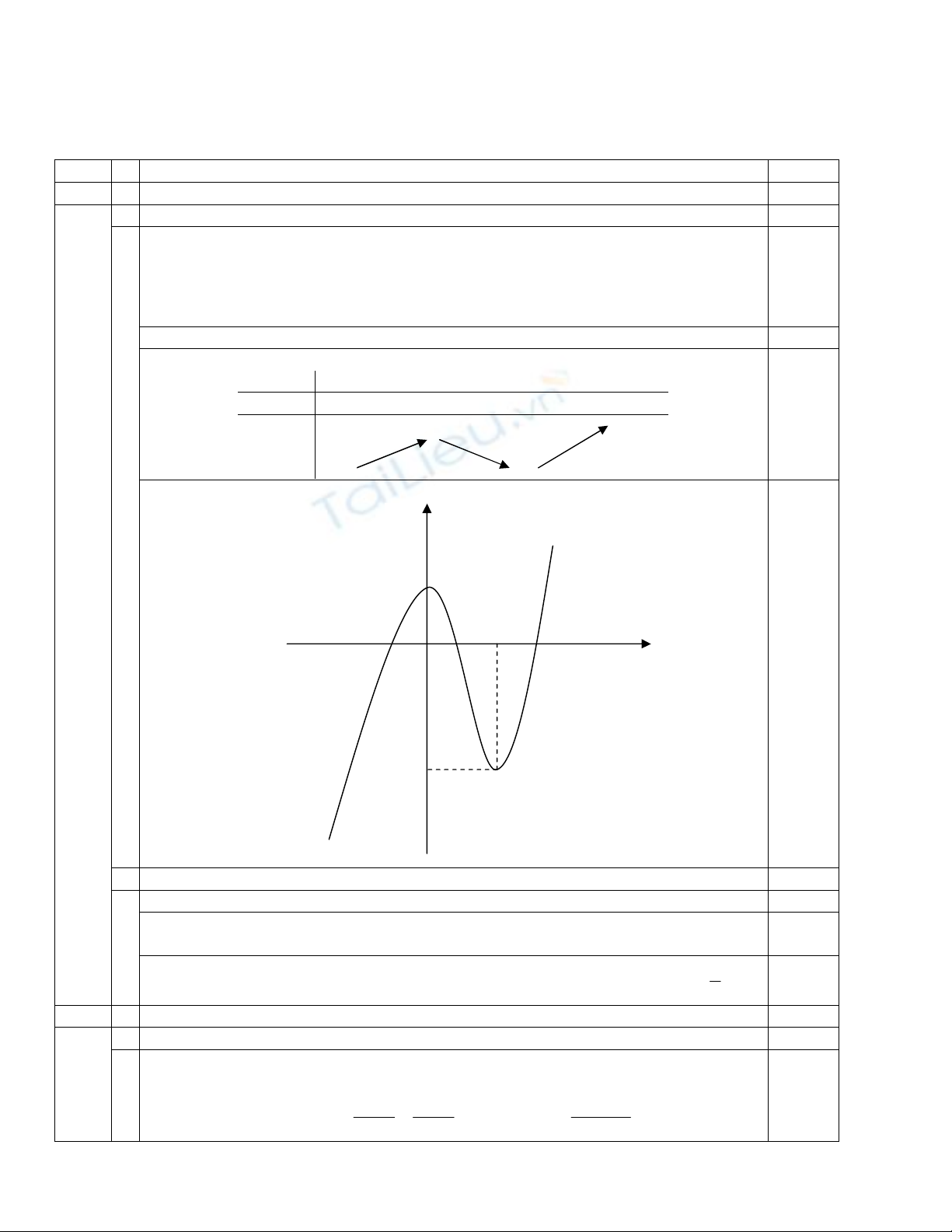
Với m = -1 hàm số trở thành y = x3 – 3x2 + 1
• Tập xác định: R
• Sự biến thiên: y’ = 3x2 – 6x; y’ = 0
2 x
0 x
0,25
• yCĐ = y(0) = 1, yCT = y(2) = -3 0,25
• Bảng biến thiên:
x -
0 2 +
y’ + 0 - 0 +
y 1 +
-
-
3
0,25
• Đồ thị:
0,25
2 Tìm các giá trị của tham số m …(1,00 điểm)
Gọi M là điểm thuộc đồ thị hàm số (1) có hoành độ x = -1, suy ra M(-1; 2m - 1) 0,25
Ta có y’ = 3x2 + 6mx + (m+1); y’(-1) = 4 – 5m. Tiếp tuyến d của đồ thị hàm số
đã cho tại M(-1; 2m – 1) có phương trình là: y = ( 4 -5m)(x + 1) + 2m – 1 0,5
Tiếp tuyến d đi qua A(1, 2) khi và chỉ khi 2 = (4 – 5m)2 + 2m – 1
m =
8
5 0,25
II 2,00
1 Giải phương trình lượng giác(1,00 điểm)
Điều kiện: sin x. cos x
0.
Phương trình đã cho tương đương với
tgx – cotgx = 4cos2 2x
sin x
xcos
x
cos
sin x = 4cos2 2x
2x
sin
2x 2cos + 4cos2 2x = 0
-3
2
1
O
x
y
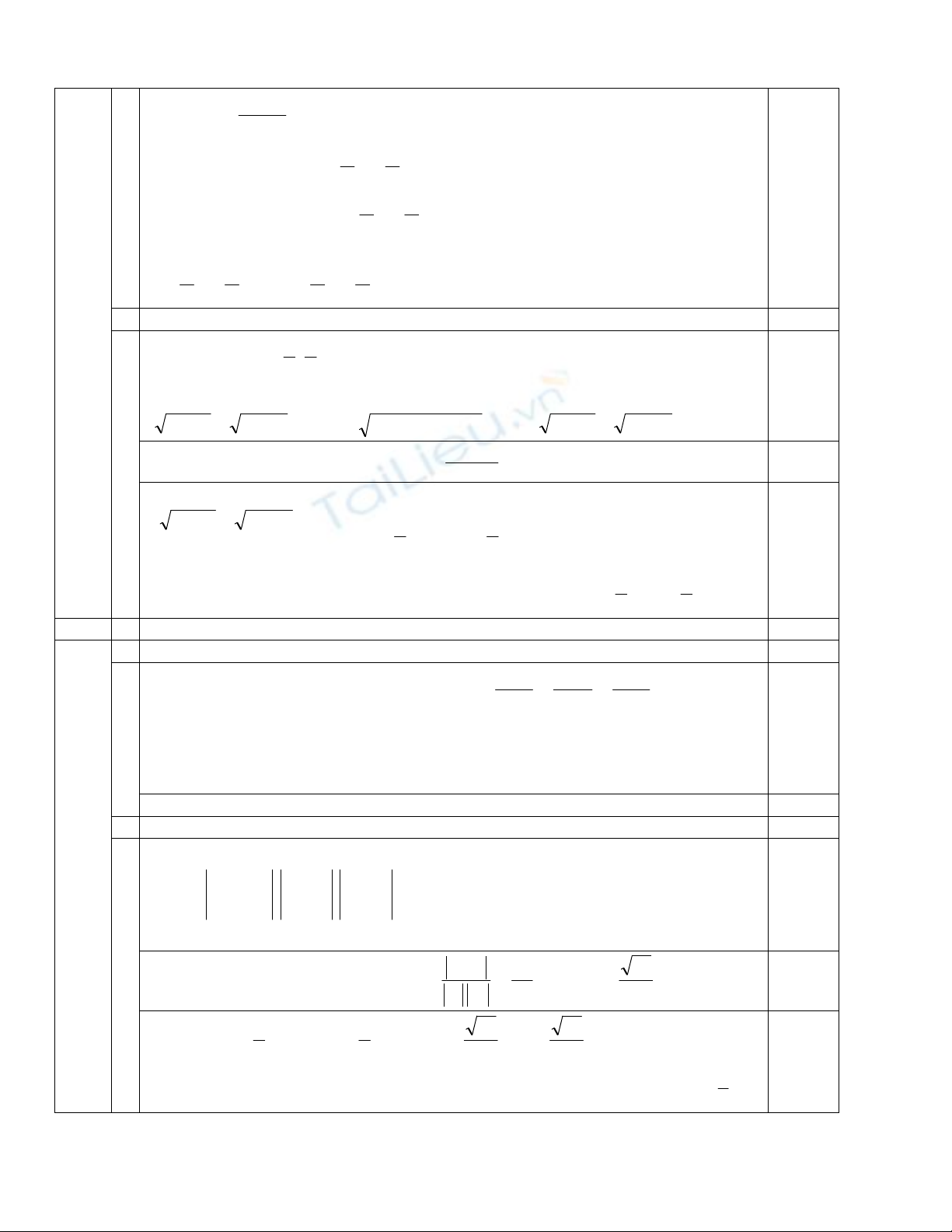
cos 2x
2x 2cos
2xsin
1 = 0
cos 2x(1 + sin 4x) = 0
.
2
4
02cos
kxx
.
2
8
14sin
kxx
Đối chiếu điều kiện suy ra nghiệm của phương trình đã cho là
2
8
2
4
kxvakx với Zk
0,50
2 Giải phương trình …(1,00 điểm)
Điều kiện:
2
3
;
2
1
x.
Ta có
2231242312242312 2 xxxxxx (1).
0,50
Mặt khác,
( ) ( )
2
22 1
2 2 1 2 2 1 4 2
2
x
x x -
- £ - £ Þ - £ Þ £
(2). 0,25
Từ (1) và (2) suy ra phương trình đã cho tương đương với
2
1
412
22312
2
x
x
xx hoặc .
2
3
x
Đối chiếu điều kiện ta được nghiệm của phương trình là
2
1
xvà
2
3
x
0,25
III 2,00
1 Chứng minh d1 cắt d2 (1,00 điểm)
Tọa độ giao điểm I của d1 và d2 thỏa mãn hệ
0766
013665 1
3
2
3
2
3
zyx
zyx
zyx
0,50
Giải hệ ta được I(1; 1; 2). 0,50
2 Tìm tọa độ…(1,00 điểm)
Véctơ chỉ phương của d1 là 1
u
= (2; 2; 1).
Ta có
61
65
;
16
56
;
66
66 = (-72; -36; -24).
Suy ra 2
u
= (6; 3; 2) là một vectơ chỉ phương của d2
0,25
Gọi α là góc giữa d1 và d2 ta có cosα =
21
21
u.u
u.u
=
21
20
sin α =
21
41 . 0,25
Ta có S IAB=
2
1IA2 sin α =
2
1IA2 sin α =
42
41 IA2 =
42
41
IA = IB = 1.
Vì A thuộc d1 nên tọa độ của A(1 + 2t; 1 + 2t; 2 + t)
IA = 3|t| = 1
t =
3
1
0,25
A
3
7
,
3
5
,
3
5 hoặc A
3
5
,
3
1
,
3
1
Vì B thuộc d2 nên tọa độ của B(1 + 6k; 1 + 3k; 2 + 2k)
IB = 7|k| = 1
t =
7
1
B
7
16
,
7
10
,
7
13 hoặc A
7
12
,
7
4
,
7
1
0,25
IV 2,00
1 Tính tích phân…(1,00 điểm)
I =
3
2
132 2x
xdx
Đặt t = 32 2x
x =
2
2t3
dx =
2
dtt3 2
x = -
2
1
t = 1; x = 3
t = 2
0,50
Suy ra I =
2
1
4
2
1
23
t2t
4
3
t2
dtt3
.
2
2t
dt =
4
3
1
2
t
5
t2
5
=
5
12
0,50
2 Giải phương trình…(1,00 điểm)
Điều kiện: cosx≠0.
Dễ thấy sinx=0 không thỏa mãn phương trình
Phương trình đã cho tương đương với
x
e
x
e
x
x
e
xx
xx
cos
sin
cos
sin 2
cos2
2
sin2
2
cossin2
(1).
Đặt
xv
xu
cos
sin . Ta có
0.;1;1, vuvu .
Từ (1) ta có phương trình
v
e
u
e
vu
2
2
2
2
.
0,50
Xét hàm số
x
e
xfy
x
2
2
)( , với
1;00;1 x.
0
2
22
1
2
2
2
2
2
2
2
2
'
x
ex
x
e
x
y
x
x
suy ra hàm số nghịch biến trên các
khoảng (-1;0) và (0;1).
Ta thấy u,v cùng dấu nên u, v cùng thuộc một khoảng (-1;0) hoặc (0;1).
Từ giả thiết f(u) = f(v)
u = v
tgx = 1
kx
4
.
Đối chiếu với điều kiện ta được nghiệm của phương trình đã cho là
kx
4
với Zk
.
0,50
V.a 2,00
1 Có bao nhiêu số tự nhiên…(1,00 điểm)
Số tự nhiên chẵn gồm 4 chữ số khác nhau của E có dạng: abcd , trong đó
4,2,0,0 da .
Xét d=0. Khi đó các số có 3 chữ số abc bằng 120
3
6A.
Xét d = 2 (hoặc d = 4), khi đó a có 5 cách chọn, ứng với mỗi cách chọn a ta có 5
cách chọn b, ứng với mỗi cách chọn hai chữ số a, b ta có 4 cách chọn chữ số c.
Vậy có tất cả 5.5.4 = 100 số.
Vậy có 120 + 100.2 = 320 số.
0,50
2 Tìm tọa độ các đỉnh…(1,00 điểm)
Gọi d1 ,d2 lần lượt là đường cao kẻ từ đỉnh B và đường phân giác trong của góc A
Gọi M’(a; b) là điểm đối xứng của M qua d2 và I là trung điểm của MM’.
Ta có
2
2
;
2
,2;
'ba
IbaMM . Vectơ chỉ phương của d2 là
1;1u.
Ta có hệ:
1
1
01
2
2
2
02
0.
2
'
b
a
ba
ba
dI
uMM
0,25
Khi đó M’(1 ; 1) thuộc đường thẳng AC. Mặt khác vectơ chỉ phương
3;4 v
của đường cao d1 chính là vectơ pháp tuyến của đường thẳng AC. Do đó phương
trình đường thẳng AC là 4(x - 1) – 3(y - 1) = 0
4x – 3y – 1 = 0.
ACdA 2xác định bởi hệ 1 0
4
5
4 3 1 0
x y x
y
x y
- + =ì ì
=
ï ï
ï ï
Û
í í
=
- - =
ï ï
ïï îî .Vậy
( )
4;5
A
0,25
Phương trình đường thẳng AB:
.0843
3
2
4
2
5
2
0
4
0
yx
yxyx
ABdB 1xác định bởi hệ
3
3 4 10 0
1
.
3 4 8 0
4
x
x y
x y y
= -ì
ï
ì + + = ï
ï
ï ï
Û
í í
- + = = -
ï ï
ï
îï
ï
î
Vậy
1
( 3; )
4
B- -
0,25
Đường thẳng AC: 4x – 3y – 1 = 0, do đó .
3
14
;
c
cC
.
25
33
;
25
31
1;1
25
31
1
22
3
14
2
2
12
2
C
C
c
c
c
cMC
Ta nhận thấy 1
AC và 2
AC cùng chiều.
Kết luận:
.1;1,
4
1
;3,5;4 CBA
Hoặc
.
25
33
,
25
31
,
4
1
;3,5;4
CBA
0,25
V.b
1 Giải bất phương trình logarit …(1,00 điểm)
Bất phương trình đã cho tương đương với
2
1
32
11
1
32
log0 2
x
x
x
x
0,50