1
ĐỀ ÔN TẬP SỐ 2 THI ĐẠI HỌC, CAO ĐẲNG
Môn thi: TOÁN, khối D
Thời gian làm bài 180 phút, không kể thời gian phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I (2 điểm) Cho hàm số 3 2
3 2
y x x mx
(1).
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 0.
2. Tìm các giá trị của m để hàm số (1) đồng biến trên khoảng (0; 2).
Câu II (2 điểm) 1. Giải phương trình 2
2
2
sin .
1 2 4
tg x tgx x
tg x
2. Tìm tất cả các giá trị của tham số m để phương trình 2
42 4 1
có đúng
một nghiệm thực.
Câu III (2 điểm) Trong không gian với hệ tọa độ Oxyz, cho điểm A(5; 5; 0) và đường thẳng
117
: .
2 3 4
x y z
d
1. Tìm tọa độ điểm A’ đối xứng với điểm A qua đường thẳng d.
2. Tìm tọa độ các điểm B, C thuộc d sao cho tam giác ABC vuông tại C và BC =
29
.
Câu IV (2 điểm) 1. Tính tích phân 12
0
( 1) x
I x x e dx
.
2. Giải hệ phương trình
2 2
2 2
2 2
36 60 25 0
36 60 25 0
36 60 25 0
x y x y
y z y z
z x z x
PHẦN RIÊNG. Thí sinh chỉ được làm 1 trong 2 câu: V.a hoặc V.b
Câu V.a Theo chương trình KHÔNG phân ban (2 điểm)
1. Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau mà mỗi số đều lớn hơn 2500.
2. Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ các đỉnh của tam giác ABC biết rằng
đường thẳng AB, đường cao kẻ từ A và đường trung tuyến kẻ từ B lần lượt có phương
trình là x + 4y – 2 = 0, 2x – 3y + 7 = 0 và 2x + 3y – 9 = 0.
Câu V.b Theo chương trình phân ban (2 điểm)
1. Giải phương trình
5 1 2 5 1 3.2 .
x x
x
2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a
và SA vuông góc với mặt phẳng đáy. Mặt phẳng qua A vuông góc với SC cắt SB, SC lần
lượt tại H, K. Tính theo a thể tích khối tứ diện SAHK.
2
ĐÁP ÁN – THANG ĐIỂM
Môn: TOÁN (đề số 2), khối D
Câu
Nội dung Điểm
I 2,00
1
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1,00 điểm)
Khi m = 0 hàm số trở thành 3 2
3 2.
y x x
Tập xác định :
.
Sự biến thiên: ' 2 '
3 6 ; 0 0
y x x y x
hoặc
2
x
.
0,25
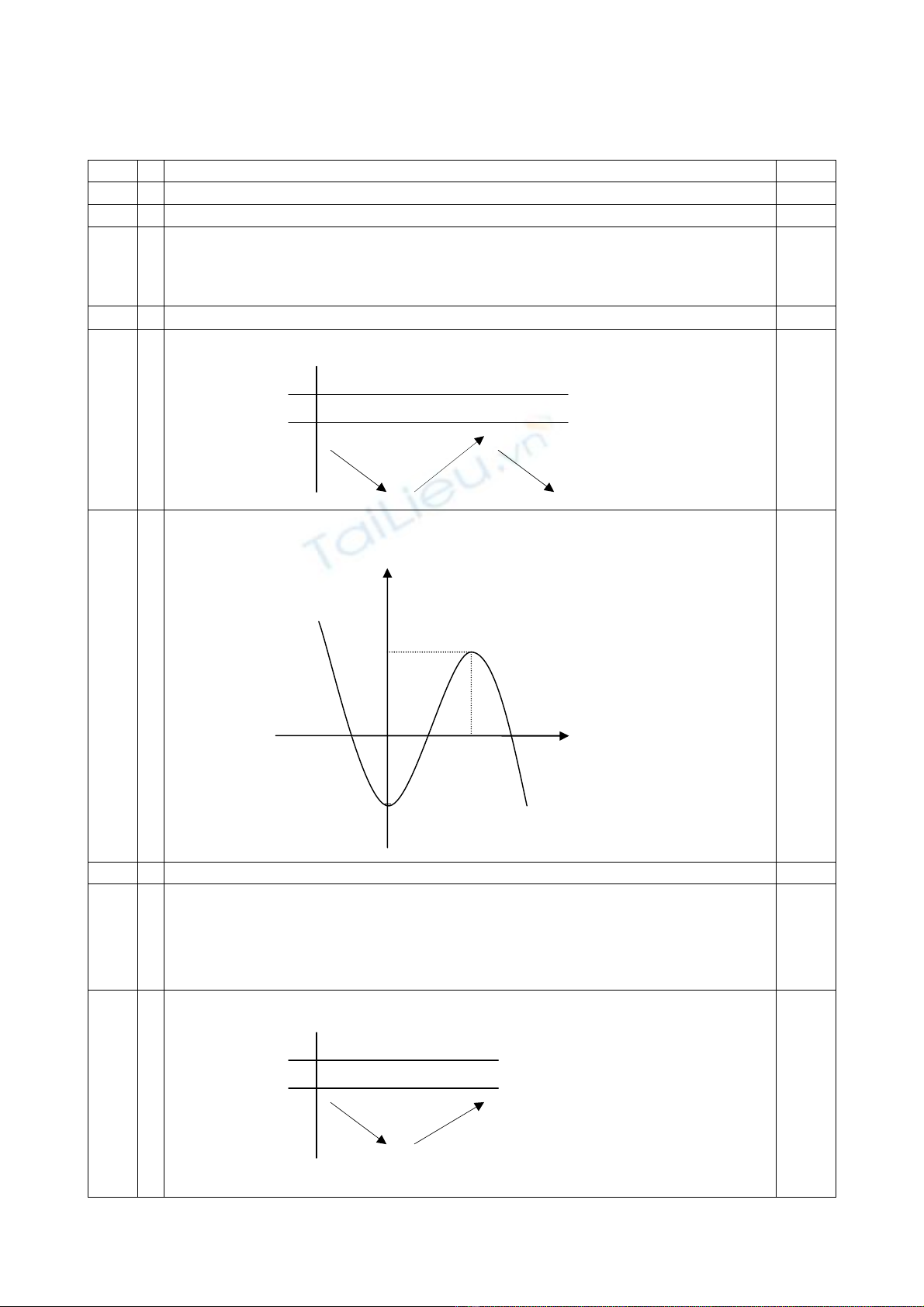
yCT = y(0) = -2, yCĐ = y(2) = 2. 0,25
Bảng biến thiên:
0,25
Đồ thị:
0,25
2
Tìm các giá trị của m…(1,00 điểm)
Ta có
' 2
3 6 .
y x x m
Hàm số đồng biến trên (0; 2) khi và chỉ khi '
0 (0;2)
y x
2
3 6 (0;2).
m x x x
0,50
Xét hàm số 2
( ) 3 6
g x x x
với x (0; 2). Ta có bảng biến thiên
Từ bảng biến thiên suy ra các giá trị cần tìm là m ≥ 0.
0,50
x
g
’
(x)
0
+
0
2
0
1
0
3
g(x)
x
'
y
y


+


2
0
2
0
0
2
-2
0
2
y
1
2 x
3
II 2,00
1
Giải phương trình lượng giác (1,00 điểm)
Điều kiện : cosx 0.
Phương trình đã cho tương đương với
2
2
2( )
sin cos
1
tg x tgx
x x
tg x
2 2 2
2cos ( ) sin cos 2sin 2sin cos sin cos
x tg x tgx x x x x x x x
(sin cos )(2sin 1) 0.
x x x
0,50
sin cos 0 1 .
4
x x tgx x k
1 5
2sin 1 0 sin 2 2 .
2 6 6
x x x k hay x k
Đối chiếu với điều kiện ta được nghiệm của phương trình là
5
2 2 .
4 6 6
x k x k x k k
Z
0,50
2
Tìm tất cả các giá trị của tham số m…(1,00 điểm)
Đặt
1 0
t x
, phương trình đã cho trở thành 44
3 (*).
t t m
Ta thấy ứng với mỗi nghiệm không âm của phương trình (*) có đúng một
nghiệm của phương trình đã cho, do đó phương trình đã cho có đúng một
nghiệm khi và chỉ khi phương trình (*) có đúng một nghiệm.
0,50
Xét hàm số 44
( ) 3
f t t t
với t ≥ 0, ta có
3
/
3
4
4
( ) 1 0
3
t
f t
t
.
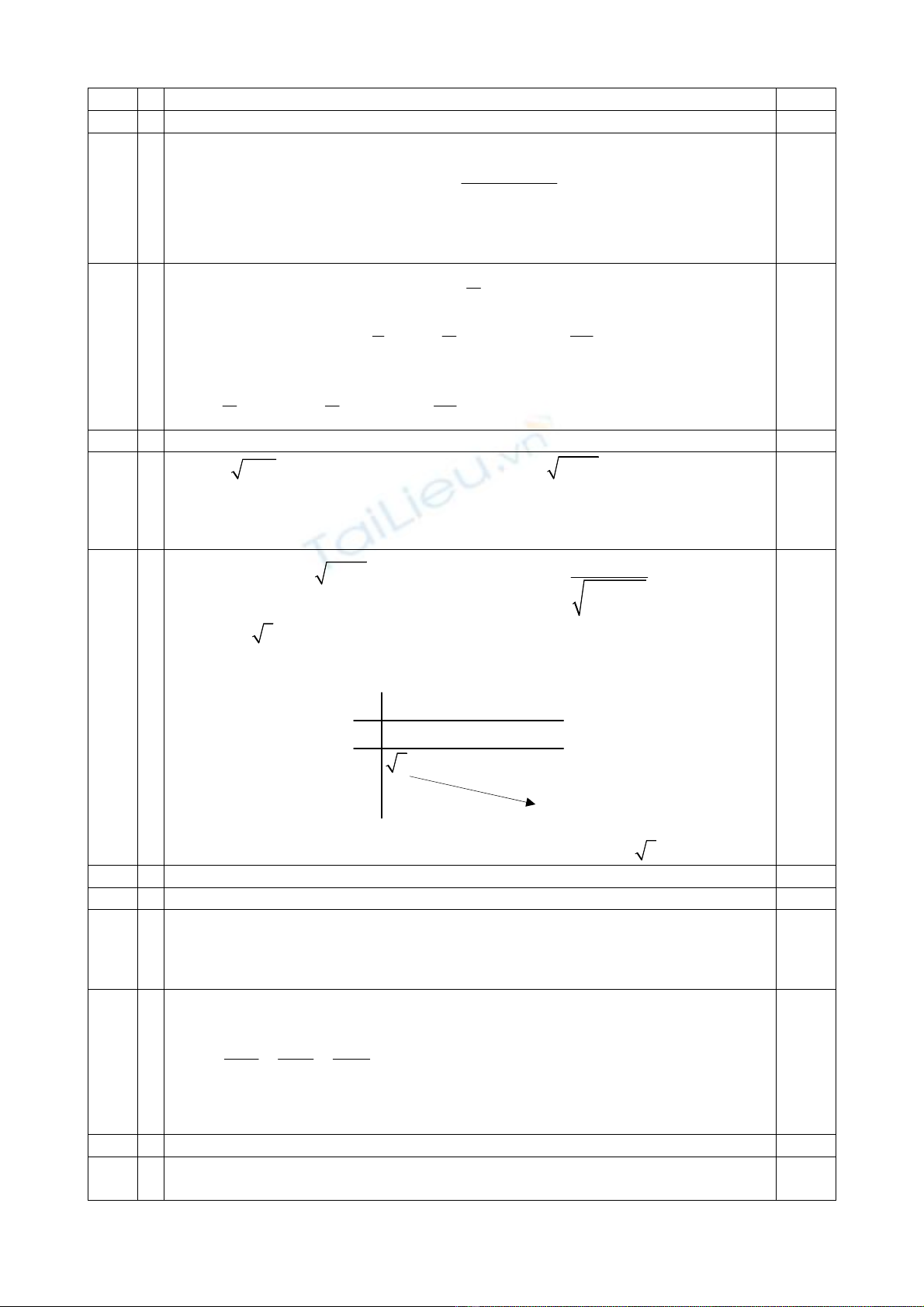
Mà f(0) = 4
3
và
lim ( ) 0.
xf t

Nên ta có bảng biến thiên:
Từ bảng biến thiên suy ra các giá trị cần tìm của m là 4
0 3
m .
0,50
III
1
Tìm tọa độ điểm A’ đối xứng với điểm A qua d…(1,00 điểm)
Đường thẳng d có vectơ chỉ phương
(2;3; 4)
u
. Mặt phẳng (P) đi qua A
vuông góc với d nhận
u
làm vectơ pháp tuyến nên có phương trình
(P): 2(x – 5) + 3(y – 5) – 4(z – 0) = 0 2x + 3y – 4z – 25 = 0.
0,50
Gọi H là trung điểm của AA’ (cũng là hình chiếu vuống góc của A trên d). Khi
đó H là giao điểm của AA’ và (P) nên có tọa độ xác định bởi
hệ
1 1 7
:
2 3 4
2 3 4 25 0.
x y z
d
x y z
Giải hệ trên ta được H(3; 5; - 1), suy ra A’(1; 5; -2).
0,50
2
Tìmđiểm B, C thuộc d… (1,00 điểm)
Vì C d và AC d nên C H(3; 5; -1) (hình chiếu vuông góc của A trên d).
0,25
t
f
’
(t)
0
4
3

f(t)
0
4
B d nên B(-1 + 2t; -1 + 3t; 7 – 4t).
2 2 2
2
29 (2 4) (3 6) (8 4 ) 29
4 3 0 1 3
BC t t t
t t t t
Do đó B {(1; 2; 3), (5; 8; -5)}.
0,50
Kết luận: C(3; 5; -1), B {(1; 2; 3), (5; 8; -5)}. 0,25
IV
1
Tính tích phân (1,00 điểm)
Đặt
21
(2 1) ,
x
u x x
du x dx
dv e dx
chọn
x
v e
1 1
2
0 0
1
( 1) (2 1) 3 1 (2 1) .
0
x x x
I x x e x e d x e x e dx
0,50
Tính 1
0
(2 1) .
x
J x e dx
Đặt 2 1
2 ,
x
u x
du dx
dv e dx
chọn
x
v e
1
0
1
(2 1) 2 3 1 2 2 1
0
x x
J x e e dx e e e
Do đó I = 2e – 2 .
0,50
2
Giải hệ phương trình
Hệ phương trình đã cho tương đương với
2
2
2
2
2
2
60
36 25
60
36 25
60
.
36 25
x
yx
y
zy
z
xz
Từ hệ suy ra x, y, z không âm.
Nhận thấy nếu x = 0 thì y = z = 0, suy ra (0; 0; 0) là một nghiệm của hệ.
0,50
Nếu x > 0 thì y > 0, z > 0. Xét hàm số
2
2
60
( ) , 0.
36 25
t
f t t
t
Ta có
'2
2
3000
( ) 0, 0.
36 25
t
f t t
t
Do đó f(t) đồng biến trên khoảng
(0; +∞).Hệ được viết lại
( )
( )
( ).
y f x
z f y
x f z
Từ tính đồng biến của f(t) suy ra x = y = z. ( Giả sử x > y
( ) ( ) ( ) ( )
f z f x z x f y f z y z
. Vậy x >y >z > x :vô lý)
Thay vào hệ ta được
5
6
x y z
.Tập nghiệm là
555
(0;0;0), ; ;
666
.
0,50
V.a 2,00
1
Có bao nhiêu số tự nhiên… (1,00 điểm)
Gọi số thỏa mãn yêu cầu bài toán có dạng
.
abcd
Nếu a > 2, ta có 7 cách chọn a,
3
9
A
cách chọn b, c, d nên có 7
3
9
A
= 3528 cách
chọn
.
abcd
0,50
5
Nếu a = 2, ta có 5 cách chọn b,
2
8
A
cách chọn c, d nên có 5
2
8
A
= 280 cách chọn
.
abcd
Vậy số các số thỏa mãn yêu cầu bài toán là 3528 + 280 = 3808 số.
0,50
2
Tìm tọa độ các đỉnh của tam giác ABC (1,00 điểm)
Tọa độ đỉnh A là nghiệm của hệ phương trình 4 2 0
( 2;1)
2 3 7 0
x y A
x y
Tọa độ đỉnh B là nghiệm của hệ phương trình 4 2 0
(6; 1)
2 3 9 0
x y B
x y
0,50
Đường thẳng BC qua B và vuông góc với đường cao kẻ từ A nên có phương
trình là: 3(x – 6) + 2(y + 1) = 0 3x + 2y – 16 = 0.
Trung điểm AC thuộc đường trung tuyến kẻ từ B nên tọa độ điểm C là nghiệm
hệ phương trình 3 2 16 0
(2;5)
2 1
2 3 9 0
2 2
x y
C
x y
.
Kết luận: A( - 2 ; 1), B(6; -1), C(2; 5).
0,50
V.b 2,00
1
Giải phương trình…(1,00 điểm)
Phương trình đã cho tương đương với 5 1 5 1
2 3 0
2 2
x x
.
Đặt
5 1 5 1 1
0
2 2
x x
t
t
.
Phương trình trở thành 2
2
3 0 3 2 0 1 2.
t t t t hay t
t
0,50
Với t = 1 ta được 5 1
1 0
2
x
x
.
Với t = 2 ta được 5 1
2
5 1
2 log 2.
2
x
x
Tập nghiệm của phương trình là 5 1
2
0,log 2
0,50
2
Tính theo a thể tích khối tứ diện SAHK…(1,00 điểm)
Vì SA (ABC) nên SA BC. Mà AB BC, do đó BC (SAB). Suy ra AH
BC. Mặt khác AH SC nên AH (SBC). Suy ra AH SB và AH HK.
0,50