http://ductam_tp.violet.vn/
Trêng THPT NguyÔn HuÖ ®Ò thi thö ®¹i häc lÇn 1 n¨m 2011
M«n: TO¸N ; Khèi: A,B
(
Thêi gian lµm bµi: 180 phót
)
PhÇn chung cho tÊt c¶ thÝ sinh
(7,0 ®iÓm)
C©u I
(2 ®iÓm)
Cho hµm sè
2 1
1
x
y
x
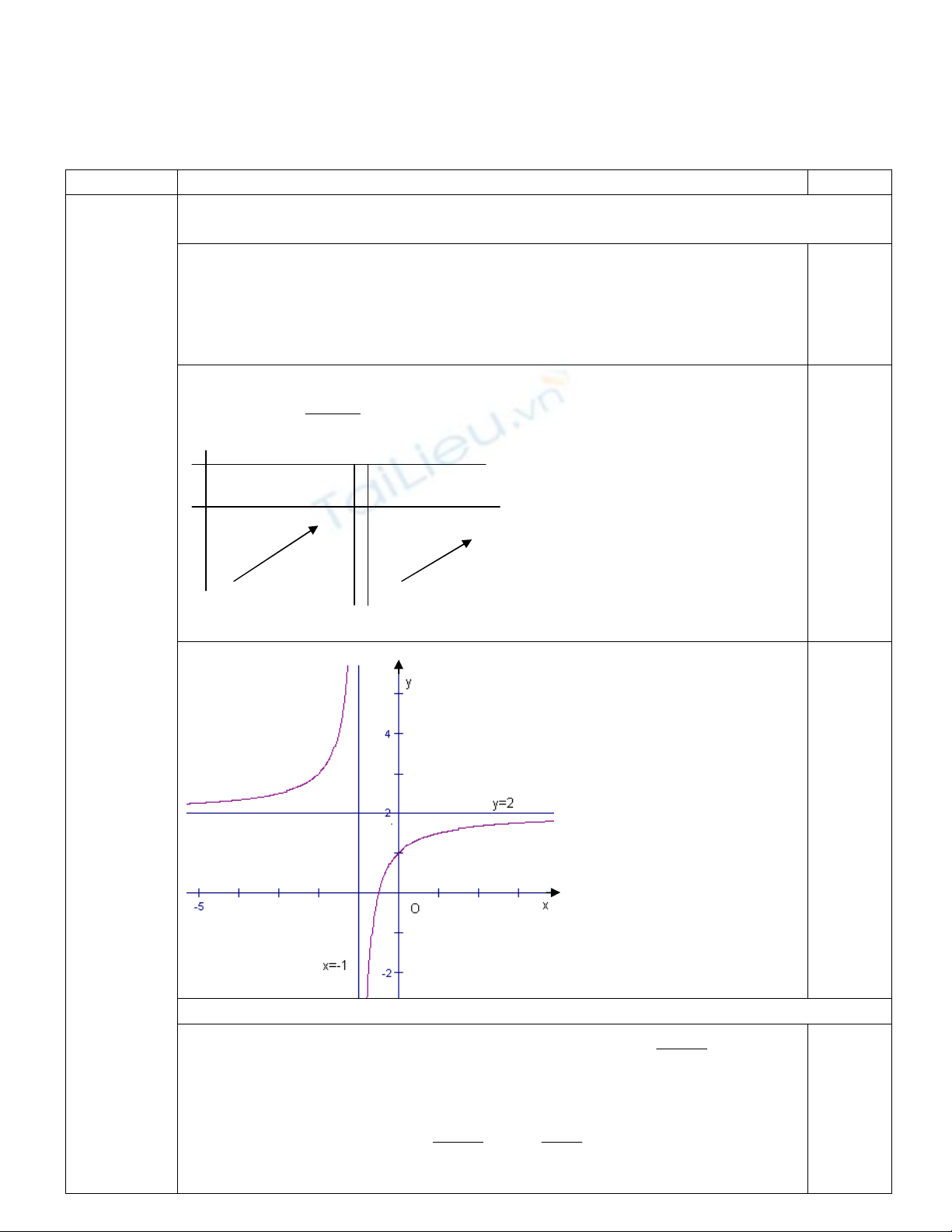
1. Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ (C) cña hµm sè ®· cho.
2. T×m trªn (C) nh÷ng ®iÓm cã tæng kho¶ng c¸ch ®Õn hai tiÖm cËn cña (C) nhá nhÊt.
C©u II
(2 ®iÓm)
1. Gi¶i hÖ ph¬ng tr×nh:
1 1 4
6 4 6
x y
x y
2. Gi¶i ph¬ng tr×nh:
1 2(cos sin )
tan cot 2 cot 1
x x
x x x
C©u III
(1 ®iÓm)
Trong mÆt ph¼ng (P) cho ®êng trßn (C) t©m O ®êng kÝnh AB = 2R.Trªn ®êng th¼ng vu«ng
gãc víi (P) t¹i O lÊy ®iÓm S sao cho OS = R
3
. I lµ ®iÓm thuéc ®o¹n OS víi SI =
2
3
R
. M lµ mét
®iÓm thuéc (C). H lµ h×nh chiÕu cña I trªn SM. T×m vÞ trÝ cña M trªn (C) ®Ó tø diÖn ABHM cã thÓ tÝch
lín nhÊt.T×m gi¸ trÞ lín nhÊt ®ã.
C©u IV
(1 ®iÓm)
TÝnh tÝch ph©n: I = 1
2
11 1
dx
x x
C©u V
(1 ®iÓm)
Cho x, y, z lµ 3 sè thùc d¬ng tháa m·n xyz=1. Chøng minh r»ng
1 1 1
1
1 1 1
x y y z z x
PhÇn riªng
(3,0 ®iÓm)
.ThÝ sinh chØ ®îc lµm mét trong hai phÇn (phÇn A hoÆc B)
A.Theo ch¬ng tr×nh ChuÈn
C©u VI.a
(1 ®iÓm)
Trong mÆt ph¼ng Oxy cho tam gi¸c ABC biÕt A(2; - 3), B(3; - 2), cã diÖn tÝch
b»ng
3
2
vµ träng t©m thuéc ®êng th¼ng
: 3x – y – 8 = 0. T×m täa ®é ®Ønh C.
C©u VII.a
(1 ®iÓm)
Tõ c¸c ch÷ sè 0,1,2,3,6,7,8,9 cã thÓ lËp ®îc bao nhiªu sè tù nhiªn cã 6 ch÷ sè
®«i mét kh¸c nhau ( ch÷ sè ®Çu tiªn ph¶i kh¸c 0) trong ®ã ph¶i cã ch÷ sè 7.
C©u VIII.a
(1 ®iÓm)
T×m a ®Ó bÊt ph¬ng tr×nh sau cã nghiÖm: 2
1 1
3 3
log 1 log ( )
x ax a
B.Theo ch¬ng tr×nh N©ng cao
C©u VI.b
(1 ®iÓm)
Trong mÆt ph¼ng Oxy cho elip (E): 2 2
1
4 3
x y
vµ ®êng th¼ng
:3x + 4y =12.
Tõ ®iÓm M bÊt k× trªn
kÎ tíi (E) c¸c tiÕp tuyÕn MA, MB. Chøng minh r»ng ®êng th¼ng AB lu«n
®i qua mét ®iÓm cè ®Þnh.
C©u VII.b
(1 ®iÓm)
Cho hµm sè
2
4 3
2
x x
y
x
cã ®å thÞ (C).Gi¶ sö ®êng th¼ng y = kx + 1 c¾t (C)
t¹i 2 ®iÓm ph©n biÖt A, B. T×m tËp hîp trung ®iÓm I cña AB khi k thay ®æi.
C©u VIII.b
(1 ®iÓm)
Gi¶i ph¬ng tr×nh:
2
2 2
log log
3 1 . 3 1 1
x x
x x
------------ -------------
http://ductam_tp.violet.vn/
Trêng THPT NguyÔn HuÖ ®¸p ¸n – thang ®iÓm
®Ò thi thö ®¹i häc lÇn 1 n¨m 2011
M«n: TO¸N ; Khèi: A,B
Lu ý:
Mäi c¸ch gi¶i ®óng vµ ng¾n gän ®Òu cho ®iÓm tèi ®a
C©u
§¸p ¸n
§iÓm
I
1.(1,0 ®iÓm) Kh¶o s¸t . . .
(2,0 ®iÓm)
* TËp x¸c ®Þnh: D = R
\
{
-
1}
* Sù biÕn thiªn
- Giíi h¹n vµ tiÖm cËn:
lim lim 2
x x
y y
 
; tiÖm cËn ngang: y = 2
( 1) ( 1)
lim ; lim
x x
y y
 
; tiÖm cËn ®øng: x = - 1
0,25
-
B¶ng biÕn thiªn
Ta cã 2
1
' 0
( 1)
yx
víi mäi x
- 1
x -
-1 +
y’ + +
y +
2
2 -
Hµm sè ®ång biÕn trªn mçi kho¶ng (-
; -1) vµ ( -1; +
)
0,5
* §å thÞ
0,25
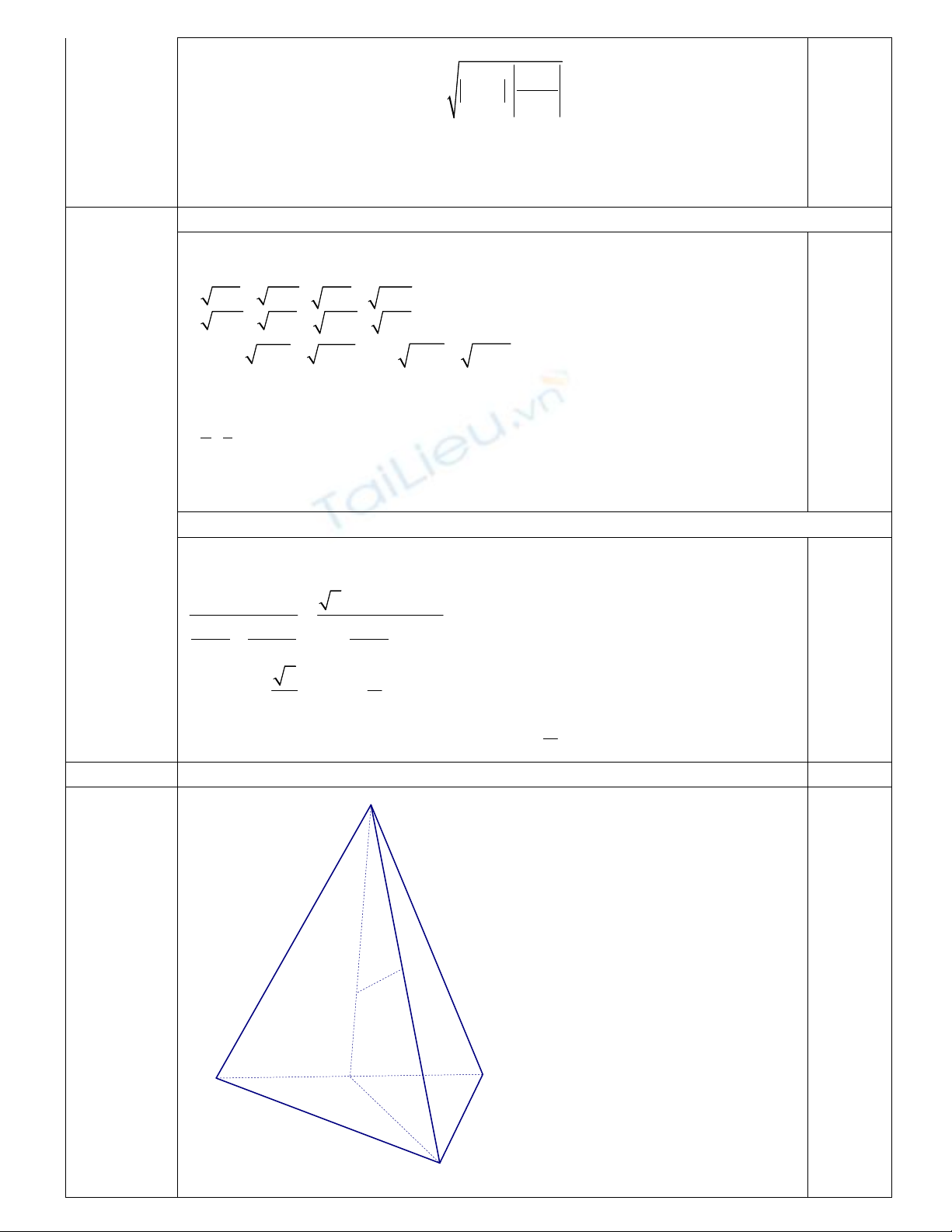
2. (1,0 ®iÓm) T×m trªn (C) nh÷ng ®iÓm. . .
Gäi M(x0;y0) lµ mét ®iÓm thuéc (C), (x0
- 1) th× 0
0
0
2 1
1
x
yx
Gäi A, B lÇn lît lµ h×nh chiÕu cña M trªn TC§ vµ TCN th×
MA = |x0+1| , MB = | y0- 2| = | 0
0
2 1
1
x
x
- 2| = | 0
1
1
x
|
0,25
0,25
http://ductam_tp.violet.vn/
Theo Cauchy th× MA + MB
2 0
0
1
x 1.
1
x
=2
MA + MB nhá nhÊt b»ng 2 khi x0 = 0 hoÆc x0 = -2.Nh vËy ta cã hai
®iÓm cÇn t×m lµ (0;1) vµ (-2;3)
0,25
0,25
II
1.(1,0 ®iÓm) Gi¶i hÖ . . .
(2,0 ®iÓm)
§iÒu kiÖn: x
-
1, y
1
Céng vÕ theo vÕ råi trõ vÕ theo vÕ ta cã hÖ
1 6 1 4 10
6 1 4 1 2
x x y y
x x y y
§Æt u=
1 6
x x
, v =
1 4
y y
. Ta cã hÖ
10
5 5
2
u v
u v
5
5
u
v
3
5
x
y
lµ nghiÖm cña hÖ
0,25
0,25
0,25
0,25
2. (1,0 ®iÓm) Gi¶i ph¬ng tr×nh . . .
§iÒu kiÖn:sinx.cosx
0 vµ cotx
1
Ph¬ng tr×nh t¬ng ®¬ng
1 2(cos sin )
sin cos2 cos 1
cos sin 2 sin
x x
x x x
x x x
cosx =
2
2
x =
2
4
k
§èi chiÕu ®iÒu kiÖn pt cã 1 hä nghiÖm x =
2
4
k
0,25
0,25
0,25
0,25
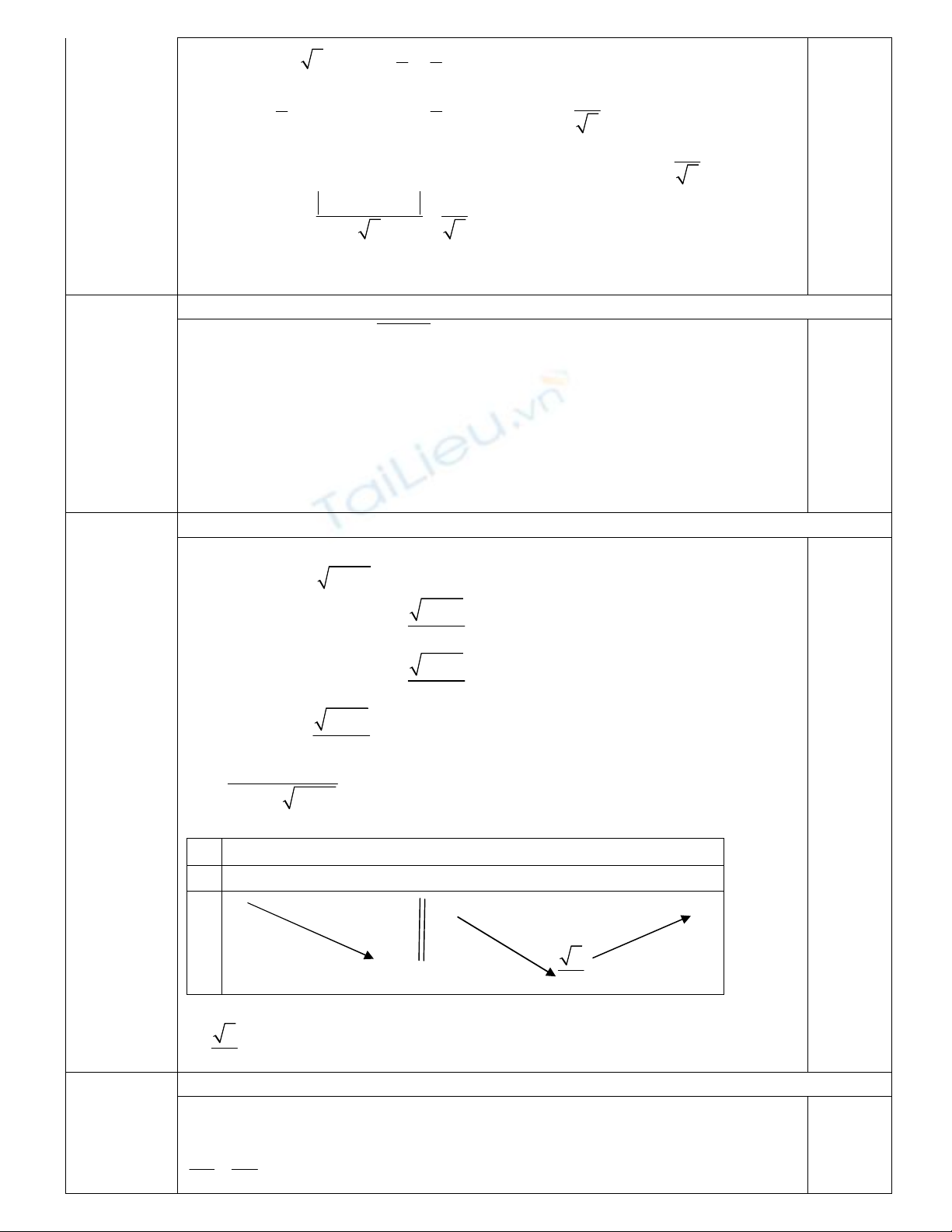
III
T×m vÞ trÝ . . .
(1,0 ®iÓm)
S
H
I
OB
M
A
http://ductam_tp.violet.vn/
Tø gi¸c IHMO néi tiÕp nªn SH.SM = SI.SO mµ OS = R
3
, SI =
2
3
R
,
SM = 2 2
2
SO OM R
SH = R hay H lµ trung ®iÓm cña SM
Gäi K lµ h×nh chiÕu vu«ng gãc cña H lªn mp(MAB) th× HK =
1
2
SO=
3
2
R ,
(kh«ng ®æi)
VBAHM lín nhÊt khi dt(
MAB) lín nhÊt
M lµ ®iÓm gi÷a cña cung AB
Khi ®ã VBAHM=
3
3
6
R
(®vtt)
0,25
0,25
0,5
IV
TÝnh tÝch ph©n . . .
(1,0 ®iÓm)
§Æt u = x+
2
1
x
th× u - x=
2
1
x
2 2 2
2 1
x ux u x
2
2
1 1 1
1
2 2
u
x dx du
u u
§æi cËn x= - 1 th× u =
2
-1
x = 1 th× u =
2
+1
2 1 2 1 2 1
2
2
2 1 2 1 2 1
1 1
11 1
2
1 2 1 2 (1 )
du
du du
u
I
u u u u
=2 1 2 1
2
2 1 2 1
1 1 1 1 1
2 1 2 1
du
du
u u u u
=1
0,25
0,25
0,25
0,25
C©u V
(1,0 ®iÓm)
§Æt x=a
3
y=b
3
z=c
3
th× x, y, z >0 vµ abc=1.Ta cã
a3 + b3=(a+b)(a2+b2-ab)
(a+b)ab, do a+b>0 vµ a2+b2-ab
ab
a3 + b3+1
(a+b)ab+abc=ab(a+b+c)>0
3 3
1 1
a b 1 ab a b c
T¬ng tù ta cã
3 3
1 1
c 1 bc a b c
b
,
3 3
1 1
a 1 ca a b c
c
Céng theo vÕ ta cã
1 1 1
1 1 1
x y y z z x
=3 3
1
a b 1
+3 3
1
c 1
b
+3 3
1
a 1
c
1 1 1 1
a b c
ab bc ca
=
1
1
a b c c a b
DÊu b»ng x¶y ra khi x=y=z=1
0,25
0,5
0,25
VI. a
T×m täa ®é . . .
http://ductam_tp.violet.vn/
(1,0 ®iÓm)
Ta cã: AB =
2
, M = (
5 5
;
2 2
), pt AB: x – y – 5 = 0
S
ABC
=
1
2
d(C, AB).AB =
3
2
d(C, AB)=
3
2
Gäi G(t;3t-8) lµ träng t©m tam gi¸c ABC th× d(G, AB)=
1
2
d(G, AB)=
(3 8) 5
2
t t
=
1
2
t = 1 hoÆc t = 2
G(1; - 5) hoÆc G(2; - 2)
Mµ 3
CM GM
C = (-2; 10) hoÆc C = (1; -4)
0,25
0,5
0,25
VII. a
Tõ c¸c ch÷ sè . . .
(1,0 ®iÓm)
Gäi sè cã 6 ch÷ sè lµ
abcdef
NÕu a = 7 th× cã 7 c¸ch chän b, 6 c¸ch chän c, 5 c¸ch chän d, 4 c¸ch
chän e, 3 c¸ch chän f. ë ®©y cã 7.6.5.4.3 = 2520sè
NÕu b = 7 th× cã 6 c¸ch chän a, 6 c¸ch chän c, 5 c¸ch chän d, 4 c¸ch
chän e, 3 c¸ch chän f. ë ®©y cã 6.6.5.4.3 = 2160sè
T¬ng tù víi c, d, e, f
VËy tÊt c¶ cã 2520+5.2160 = 13320 sè
0,25
0,5
0,25
VIII. a
T×m a ®Ó . . .
(1,0 ®iÓm)
§iÒu kiÖn: ax + a > 0
Bpt t¬ng ®¬ng 2
1 ( 1)
x a x
NÕu a>0 th× x +1 >0.Ta cã 21
1
x
a
x
NÕu a<0 th× x +1 <0.Ta cã 21
1
x
a
x
XÐt hµm sè y =
2
1
1
x
x
víi x
- 1
y’ = 2 2
1
( 1) 1
x
x x
=0 khi x=1
x -
-1 1 +
y’
- || - 0 +
y
-1 +
1
-
2
2
a>
2
2
hoÆc a < - 1
0,25
0,25
0,25
0,25
VI. b
Chøng minh . . .
(1,0 ®iÓm)
Gäi M(x
0
;y
0
), A(x
1
;y
1
), B(x
2
;y
2
)
TiÕp tuyÕn t¹i A cã d¹ng
1 1
1
4 3
xx yy
0,25