zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Đề thi - Kiểm tra

Đề ôn thi tốt nghiệp THPT môn Toán năm 2023 - Trường THPT Gò Công Đông

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:6

Báo xấu

12
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mời các bạn học sinh và quý thầy cô cùng tham khảo “Đề ôn thi tốt nghiệp THPT môn Toán năm 2023 - Trường THPT Gò Công Đông” để giúp học sinh hệ thống kiến thức đã học cũng như có cơ hội đánh giá lại năng lực của mình trước kì thi sắp tới và giúp giáo viên trau dồi kinh nghiệm ra đề thi.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề ôn thi tốt nghiệp THPT môn Toán năm 2023 - Trường THPT Gò Công Đông

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG SỞ GD&ĐT TIỀN GIANG ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023 TRƯỜNG THPT GÒ CÔNG ĐÔNG MÔN : TOÁN Thời gian làm bài: 90 phút. Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức z 2022 − 2023i có tọa độ là = A. ( −2022; 2023) . B. ( 2022; − 2023) . C. ( 2023; 2022 ) . D. ( 2023; − 2022 ) . Câu 2: Trên khoảng ( 0; + ∞ ) , đạo hàm của hàm số y = log 5 x là 1 1 ln 5 1 A. y′ = . B. y′ = . C. y′ = . D. y′ = − . x x ln 5 x x ln 5 Câu 3: Trên khoảng ( 0; + ∞ ) , đạo hàm của hàm số y = x 3 là 1 A. y′ = 3 x 3 −1 . B. y′ = x 3 −1 . C. y′ = x 3 −1 . D. y′ = 3 x 3 . 3 Câu 4: Tập nghiệm của bất phương trình log 2 x > 3 là A. ( −∞;8] . B. ( 8; +∞ ) . C. [8; +∞ ) . D. ( −∞;8 ) . Câu 5: Cho cấp số cộng ( un ) với u1 = 2 và công sai d = 3 . Giá trị của u5 bằng A. 162 . B. −10 . C. 11. D. 14 .  x= 3 + t  Câu 6: Trong không gian Oxyz , đường thẳng d :  y =−2 + t có một vectơ chỉ phương là  z= 4 + t      A. a = ( −1;1;1) . B. a (1;1; −1) . = C. a = (1;1;1) . D. a (1; −1;1) . = ax + b Câu 7: Cho hàm số y = có đồ thị là đường cong trong hình cx + d vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là A. ( 0; −2 ) . B. ( 2;0 ) . C. ( −2;0 ) . D. ( 0;2 ) . 4 4 Câu 8: Nếu ∫ f ( x ) dx = 2023 và ∫ g ( x ) dx = 2022 thì −1 −1 4 ∫  f ( x ) − g ( x )  dx −1   bằng A. 5. B. 6. C. 1. D. −1 . Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x −3 A. y =x 4 − 3 x 2 + 2 . B. y = . x −1 C. y = x 2 − 4 x + 1 . D. y = x 3 − 3 x − 5 . Câu 10: Trong không gian Oxyz cho mặt cầu (S ) có phương trình x 2 + y 2 + z 2 − 2 x + 4 y − 6 z = Tìm tọa độ tâm I và bán kính R của mặt 0. cầu ( S ) . Trang 73
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG A. I (1; −2;3) ; R = 14 . B. I ( −1; 2; −3) ; R = . 14 C. I ( −1; 2; −3) ; R = 14 . D. I (1; −2;3) ; R = 14 . Câu 11: Trong không gian Oxyz , góc giữa hai mặt phẳng ( P ) : x + y − z − 11 =0 và ( Q ) : 2 x + 2 y − 2 z + 7 = bằng 0 A. 0° . B. 90° . C. 180° . D. 45° . Câu 12: Cho số phức z  3  4i. Phần thực của số phức w  z  z là A. 8 . B. 4 . C. 5 . D. 3 . Câu 13: Cho khối lập phương có độ dài đường chéo bằng 3 3 . Thể tích khối lập phương đã cho bằng A. 9 . B. 12 . C. 27 . D. 18 . Câu 14: Cho khối chóp S . ABCD có đáy ABCD là hình chữ nhật, AB a= a 3 , SA vuông góc với = , BC đáy và SA = 2a . Thể tích khối chóp đã cho bằng 2a 3 3 a3 3 a3 3 A. . B. 2a 3 3 . C. . D. . 3 3 6 Câu 15: Cho mặt phẳng ( P ) cắt mặt cầu S ( O; R ) theo giao tuyến là đường tròn ( O; R ) . Gọi d là khoảng cách từ O đến ( P ) . Khẳng định nào dưới đây đúng? A. d < R . B. d > R . C. d = R . D. d = 0 . Câu 16: Phần thực của số phức z= 2 − 3i là A. −3 . B. −2 . C. 2. D. 3. Câu 17: Cho hình nón có đường kính đáy bằng độ dài đường sinh l . Diện tích xung quanh của hình nón đã cho bằng: 1 2 A. 2π rl . B. π l 2 . C. π r 2 . D. π r 2l . 2 3 x −1 y − 2 z + 3 Câu 18: Trong không gian Oxyz , cho đường thẳng d : = = . Vectơ nào dưới đây 2 −1 −2 không là vectơ chỉ phương của d ?      A. a = ( 4; −2; −4 ) . B. b (1; 2; −3) . = C. c = ( −2;1; 2 ) . D. d = ( 2; −1; −2 ) . Câu 19: Cho hàm số y = ax 4 + bx 2 + c có đồ thị là đường cong trong hình bên. Giá trị cực đại của đồ thị hàm số đã cho là: A. x = x = −1, 1. B. x = 0 . C. y = 2 . D. y = 1 . 2x +1 Câu 20: Tiệm cận đứng của đồ thị hàm số y = là đường thẳng có phương trình 3x − 1 1 2 1 2 A. x = . B. x = − . C. x = − . D. y = 3 3 3 3 Câu 21: Giải bất phương trình log 2 ( 3 x − 1) > 3 . 1 10 A. x > 3 B. < x 3 3 Câu 22: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 34 học sinh? Trang 74
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG A. 234 . B. A34 . 2 C. 342 . D. C34 . 2 Câu 23: Hàm số F ( x ) = e x là một nguyên hàm của hàm số 2 2 ex A. f ( x ) = e . 2x B. f ( x ) x .e − 1 . = 2 x2 C. f ( x ) = 2 xe .x2 D. f ( x ) = . 2x 5 −1 f ( x) Câu 24: Nếu ∫ f ( x ) dx = 6 thì ∫ dx bằng −1 5 3 49 A. 18. B. . C. 2. D. −2 . 8 Câu 25: Tìm họ nguyên hàm của hàm số f ( x ) = sin 2 x . 1 A. ∫ f (= x )dx cos2 x + C . B. ∫ f ( x )dx = x + C . − cos2 2 1 C. ∫ f ( x )dx = x + C . −cos2 D. ( x )dx ∫ f= 2 cos2 x + C . 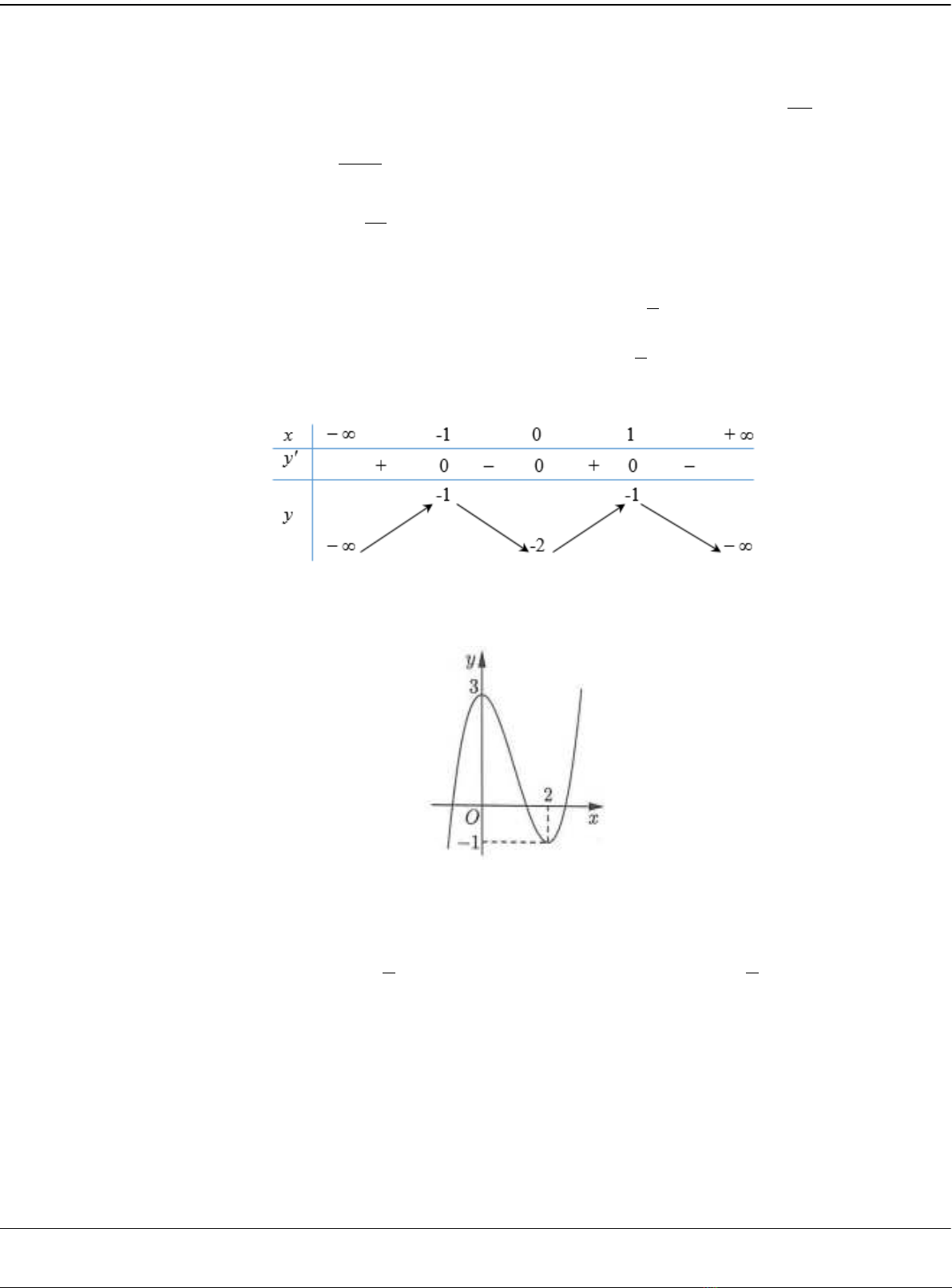Câu 26: Cho hàm số y = f ( x ) có bảng biến thiên như sau Hàm số đã cho đồng biến trên khoảng nào dưới đây? 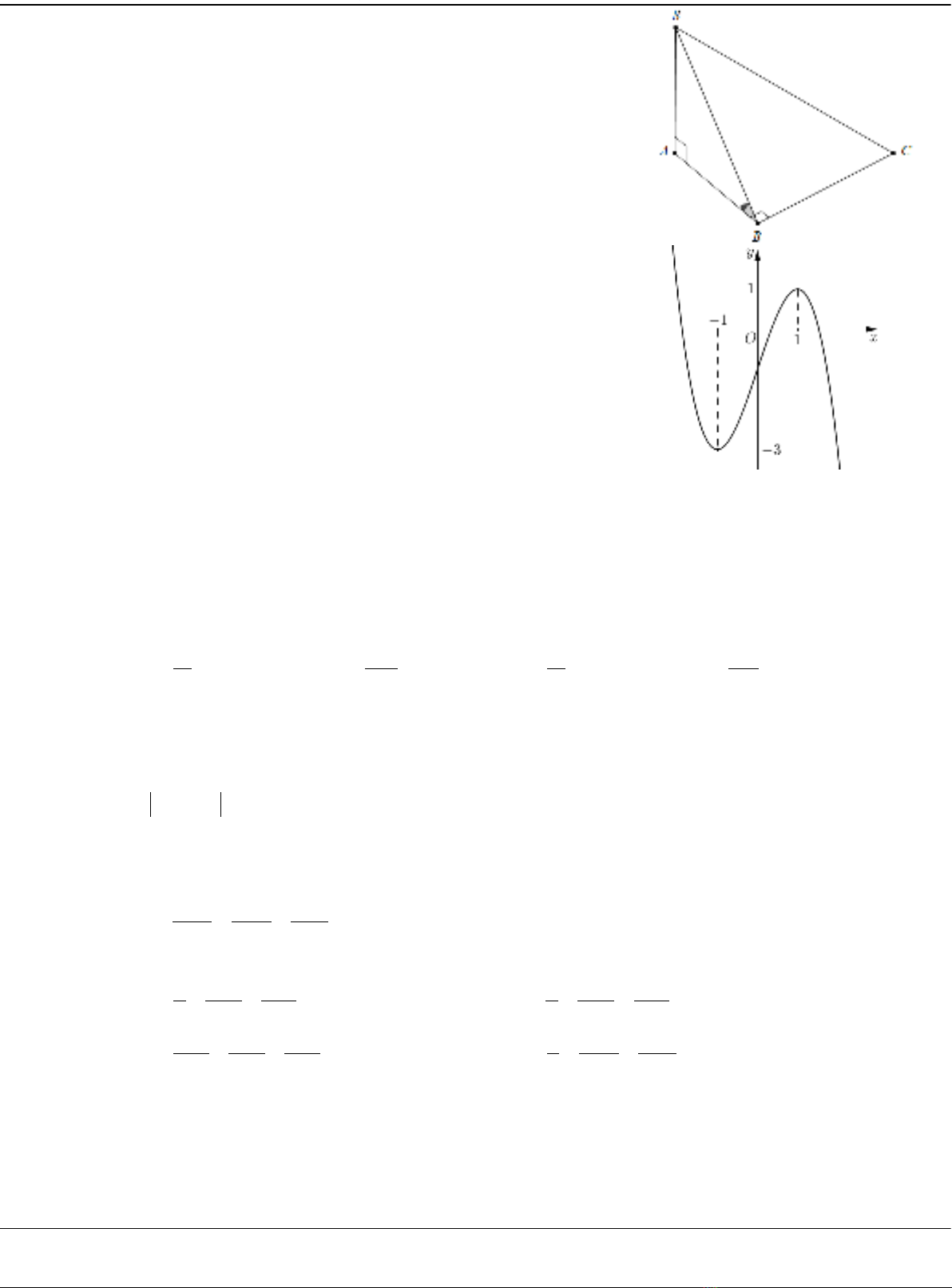Câu 27: Cho hàm số bậc ba 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) có đồ thị là đường cong trong hình bên. A. ( −1;0 ) . B. (1; +∞ ) . C. ( −∞;1) . D. ( 0;1) . Hàm số nghịch biến trong khoảng: Câu 28: Với 𝑎𝑎,b là hai số thực dương tùy ý, ln(3ab) − ln(2ab) bằng: A. (2;3) . B. (−1;3) . C. (0; 2) . D. (−1; 2) . 2 3 A. ln ab . . B. ln C. ln(6) . D. ln . 3 2 Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường = x 2 − 4 x và y y = 0 quanh trục Ox là: 4 4 2 4 A. π ∫ ( x 2 − 4 x)dx ⋅ B. π ∫ (4 x − x 2 ) 2 dx ⋅ C. π ∫ ( x 2 − 4 x) 2 dx ⋅ D. ∫ ( x 2 − 4 x) 2 dx ⋅ 0 0 −2 0 Trang 75
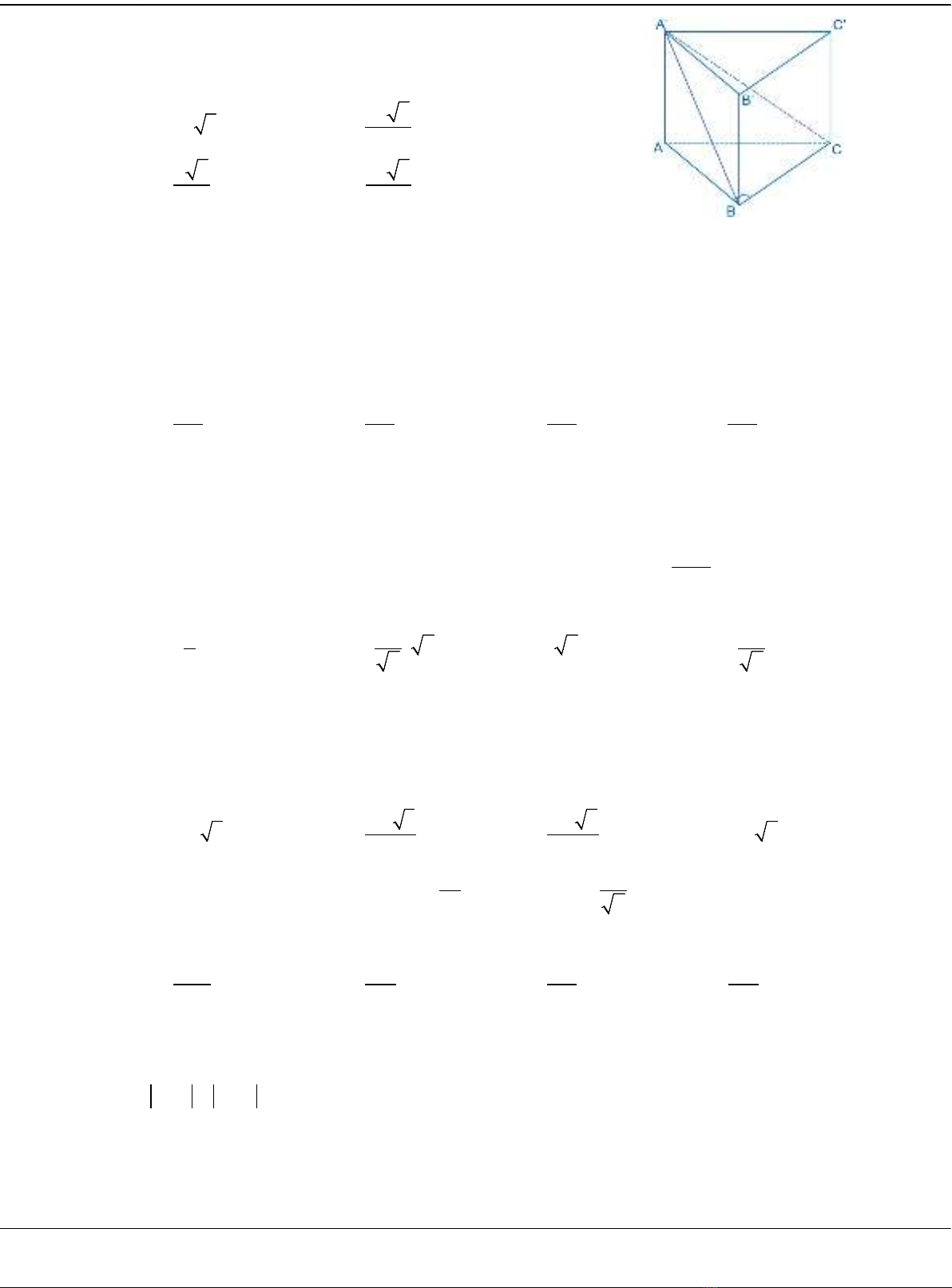
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG Câu 30: Cho hình chóp S . ABC có đáy là tam giác vuông tại B , SA vuông góc với đáy và SA = AB (tham khảo hình vẽ). Góc giữa đường thẳng SB và mặt phẳng ( ABC ) bằng A. 60°. B. 30°⋅ C. 90°⋅ D. 45°⋅ Câu 31: Cho hàm số bậc ba y = f ( x ) có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2. f ( x ) = m có ba nghiệm thực phân biệt? A. 3 . B. 7 . C. 10 . D. 8 . ( ) Câu 32: Cho hàm số y = f ( x ) có đạo hàm f ′ ( x ) =− 2 ) 9 − x 2 với mọi x ∈  . Hàm số đã cho có (x 2 bao nhiêu điểm cực đại? A. 1. B. 2 . C. 3 . D. 4 . Câu 33: Bạn Bình có 30 tấm thẻ đánh số từ 1 đến 30 , Bình chọn ngẫu nhiên 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và chỉ có một tấm thẻ mang số chia hết cho 10 . 8 99 3 99 A. . B. . C. . D. . 11 667 11 167 Câu 34: Tính tổng các nghiệm của phương trình log ( x 2 − 3 x + 1) =9 bằng − A. −3 . B. 9 . C. 10−9 . D. 3 . Câu 35: Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn của số phức z có mô đun lớn nhất thỏa mãn: z + 4 − 3i =. Tọa độ của điểm M là 5 A. M ( −6;8 ) . B. M ( 8; −6 ) . C. M ( 8;6 ) . D. M ( −8;6 ) . Câu 36: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A (1; −2; −3) ; B ( −1; 4;1) và đường thẳng x+2 y−2 z +3 d: = = . Phương trình nào dưới đây là phương trình của đường thẳng đi qua 1 −1 2 trung điểm của đoạn AB và song song với d ? x y −1 z +1 x y −1 z +1 A. = = . B.= = . 1 1 2 1 −1 2 x −1 y −1 z +1 x y−2 z+2 C. = = . D. = = . 1 −1 2 1 −1 2 Câu 37: Trong không gian Oxyz , cho điểm A(−4;1;3) . Điểm đối xứng với A qua mặt phẳng (Oxy ) có tọa độ là A. (4;1;3) . B. (4; −1;3) . C. (−4;1; −3) . D. (−4; −1; −3) . Trang 76
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG Câu 38: Một hình lăng trụ đứng ABC. A′B′C ′ có đáy ABC là tam giác vuông tại B, AB a= 2a. (tham khảo hình bên). Khoảng = , AA′ cách từ điểm A đến mặt phẳng ( A′BC ) là: 2a 5 A. 2a 5 . B. . 5 a 5 3a 5 C. . D. . 5 5 Câu 39: Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình log 3 ( 3 x + m ) > 3log 3 x chứa đúng 2 số nguyên? A. 18 . B. 15 . C. 17 . D. 16 . Câu 40: Hàm số f ( x ) = ax3 + bx 2 + cx + d có f ( 0 ) = 2 và f ( 4 x ) − f ( x= 4 x3 + 2 x, ∀x ∈ . Tích phân ) 1 I = ∫ f ( x ) dx bằng 0 148 146 149 145 A. . B. . C. . D. . 63 63 63 63 Câu 41: Có bao nhiêu số nguyên m để hàm số y = 5 x 6 + 18mx5 + 15 ( m 2 − 3m + 2 ) x 4 + 1 chỉ có điểm cực tiểu mà không có điểm cực đại? A. 28 . B. 27 . C. 25 . D. 26 . 1 + iz Câu 42: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức w = là một đường tròn có 1+ z bán kính bằng 2 . Môđun của z thuộc tập nào dưới đây? 1   1  1  A.  ; 2  . 2  B.   2  ; 2 .  C. { } 2; 2 . D.  ; 2 .  2  Câu 43: Cho khối lăng trụ ABC. A′B′C ′ có đáy là tam giác đều, góc giữa hai mặt phẳng ( A′B′C ′ ) và ( BCC ′B′) bằng 60° , hình chiếu vuông góc của B′ lên mặt phẳng ( ABC ) trùng với trọng tâm tam giác ABC . Khoảng cách giữa hai đường thẳng AA′ và B′C ′ bằng 3a . Thể tích khối lăng trụ đã cho bằng 8a 3 3 8a 3 6 A. 8a 3 3 . B. . C. . D. 8a 3 6 . 3 3 23  1  Câu 44: Cho hàm số f ( x ) thỏa mãn f ( 4 ) = và f ( x ) = x 1 + − f ′ ( x )  , ∀x > 0 . Diện tích hình 6  x  phẳng giới hạn bởi đồ thị hàm số g ( x) = xf ( x ) , trục hoành, đường thẳng = 1; x 4 bằng x = 1283 743 157 563 A. . B. . C.. D. . 30 30 30 30 Câu 45: Trên tập hợp số phức, xét phương trình z 2 + 2 ( m + 1) z + 12m − 8 = ( m là tham số thực). Có 0 bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt z1 , z2 thỏa mãn z1 + 1 = z2 + 1 ? A. 7 . B. 12 . C. 8 . D. 9 . Trang 77
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG x −1 y z − 2 Câu 46: Trong không gian Oxyz , cho đường thẳng d1 : = = và đường thẳng 2 1 2 x y − 2 z +1 2 : d= = . Gọi ( P ) là mặt phẳng chứa đường thẳng d1 và song song với d 2 . Tính 1 1 2 khoảng cách giữa đường thẳng d 2 và mặt phẳng ( P ) . 1 7 A. . B. 7 5 . C. . D. 5. 5 5 5 5 Câu 47: Có bao nhiêu cặp số nguyên dương ( x; y) thỏa 3 ( 81y + 4 y ) + 2026 ≤ − x 2 + 2024 x + log 3 ( x − 2023)3 (1 − x)3  ?   A. 2021 . B. 2003 . C. 4042 . D. 4024 . Câu 48: Cho khối nón đỉnh S , bán kính đáy bằng 3 3 và có góc ở đỉnh bằng 120 . Gọi A và B là hai điểm thuộc đường tròn đáy sao cho tam giác SAB là tam giác vuông, khoảng cách từ tâm đường tròn đáy đến mặt phẳng ( SAB) bằng 3 3 2 A. 3 . B. . C. . D. 3. 2 2 x −1 y − 2 z − 3 Câu 49: Trong không gian Oxyz cho đường thẳng d : = = và mặt cầu 2 3 4 ( S ) : ( x + 3)2 + ( y + 4 )2 + ( z + 5)2 = . Cho biết điểm A ( −2; −2; −7 ) , điểm B thuộc giao 729 tuyến của mặt cầu ( S ) và mặt phẳng ( P ) : 2 x + 3 y + 4 z − 107 =Khi điểm M di động trên 0. đường thẳng d , giá trị nhỏ nhất của biểu thức MA + MB bằng A. 5 30 . B. 27 . C. 5 29 . D. 742 . Câu 50: Cho hàm số y = f ( x ) có đạo hàm liên tục trên  . Hàm số y = f ′ ( x ) có đồ thị như hình vẽ. Xét hàm số g ( x )= 3 f ( − x3 − 3 x + m ) + ( x3 + 3 x − m ) ( −2 x3 − 6 x + 2m − 6 ) . Số giá trị nguyên của 2 tham số m thuộc đoạn [ −2023; 2023] để hàm số g ( x ) nghịch biến trên khoảng ( −2; 2 ) là A. 4019 . B. 2023 . C. 2008 . D. 4029 . Trang 78

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.