1
SỞ GD & ĐT KON TUM
TRƯỜNG THPT TRƯỜNG CHINH
ĐỀ KIỂM TRA GIỮA KÌ I, NĂM HỌC 2023 - 2024
Môn thi: Toán - Lớp 10
Thời gian: 90 phút (không kể thời gian phát đề)
Đề gồm 06 trang: 35 câu trắc nghiệm, 03 câu tự luận
I. PHẦN TRẮC NGHIỆM (7,0 điểm)
Câu 1. Trong các câu sau, câu nào là mệnh đề toán học?
A. n là một số chia hết cho 2.
B. 3 là một số nguyên.
C. Kon Tum là một tỉnh nằm ở phía bắc Tây Nguyên Việt nam.
D. 2023 có phải là một số lẻ không?
Câu 2. Khẳng định nào sau đây đúng?
A. Hai vectơ bằng nhau nếu chúng có cùng độ dài.
B. Hai vec tơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
C. Hai vec tơ bằng nhau nếu chúng ngược hướng và cùng độ dài.
D. Hai vec tơ bằng nhau nếu chúng cùng phương và cùng độ dài.
Câu 3. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một
điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách
40mAB ,
฀
0
45CAB và
฀
0
70CBA .
Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?
A. 53 m. B. 30 m . C. 41,5 m . D. 41 m .
Câu 4. Cho hai mệnh đề :P “Tam giác ABC có AB AC” và :Q “Tam giác ABC cân tại A”. Phát biểu
mệnh đề P Q là mệnh đề nào dưới đây?
A. Tam giác ABC cân tại A khi và chỉ khi AB AC.
B. Nếu tam giác ABC có AB ACthì tam giác ABC cân tại A.
C. Tam giác ABC có AB AC nếu và chỉ nếu tam giác ABC cân tại A.
D. Nếu tam giác ABC cân tại A thì AB AC.
Câu 5. Cho
; ; .X a b c Các tập con có hai phần tử của tập X là
A. ( ; );( ; );( ; )a b a c b c . B.
; ; ;a b b c .
C.
; ; ; ;{ ; }a b a c a d . D.
; ;{ ; }; ;a b a c b c .
ĐỀ CHÍNH THỨC
MÃ ĐỀ: 101
Trang 1/6 -Mã đề 101
2
Câu 6. Một gian hàng trưng bày bàn và ghế rộng 2
60m. Diện tích để kê một chiếc bàn là 2
1,2m, một chiếc
ghế là 2
0,5m. Gọi x là số chiếc bàn, y là số chiếc ghế được kê. Viết bất phương trình bậc nhất hai ẩn ,x y
cho phần mặt sàn để kê bàn và ghế biết diện tích mặt sàn để lưu thông tối thiểu là 2
12m.
A. 1,2 0,5 60x y . B. 1,2 0,5 12x y .
C. 1,2 0,5 48x y . D. 1,2 0,5 48x y .
Câu 7. Cho tập hợp
1;2;3;4X. Khẳng định nào sau đây đúng?
A.
1X. B. 2X. C. 3X. D. 4X.
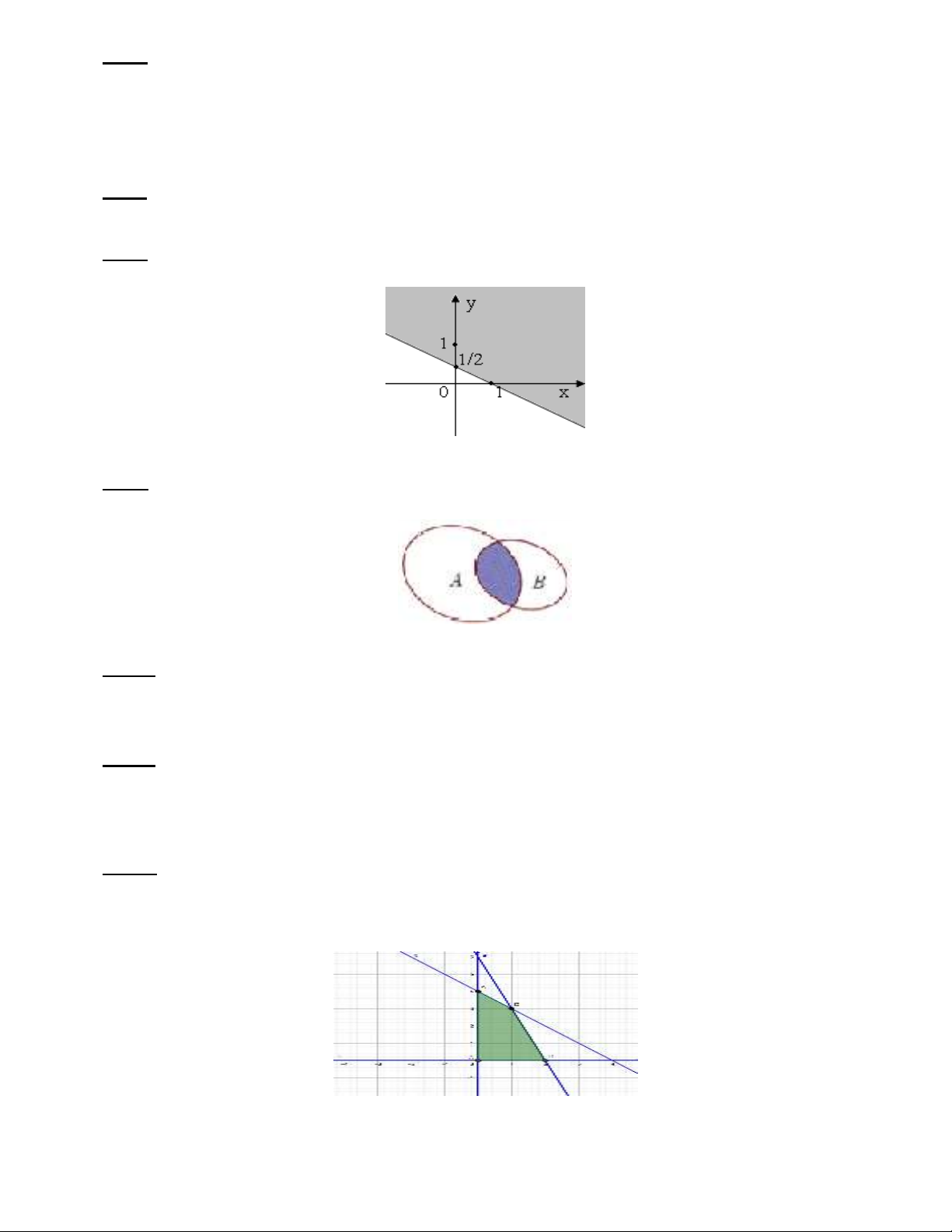
Câu 8. Phần mặt phẳng không bị tô đậm (lấy cả đường thẳng) trong hình vẽ sau đây biểu diễn miền nghiệm
của bất phương trình nào?
A. 2 1x y . B. 2 1x y . C. 2 1x y . D. 2 1x y .
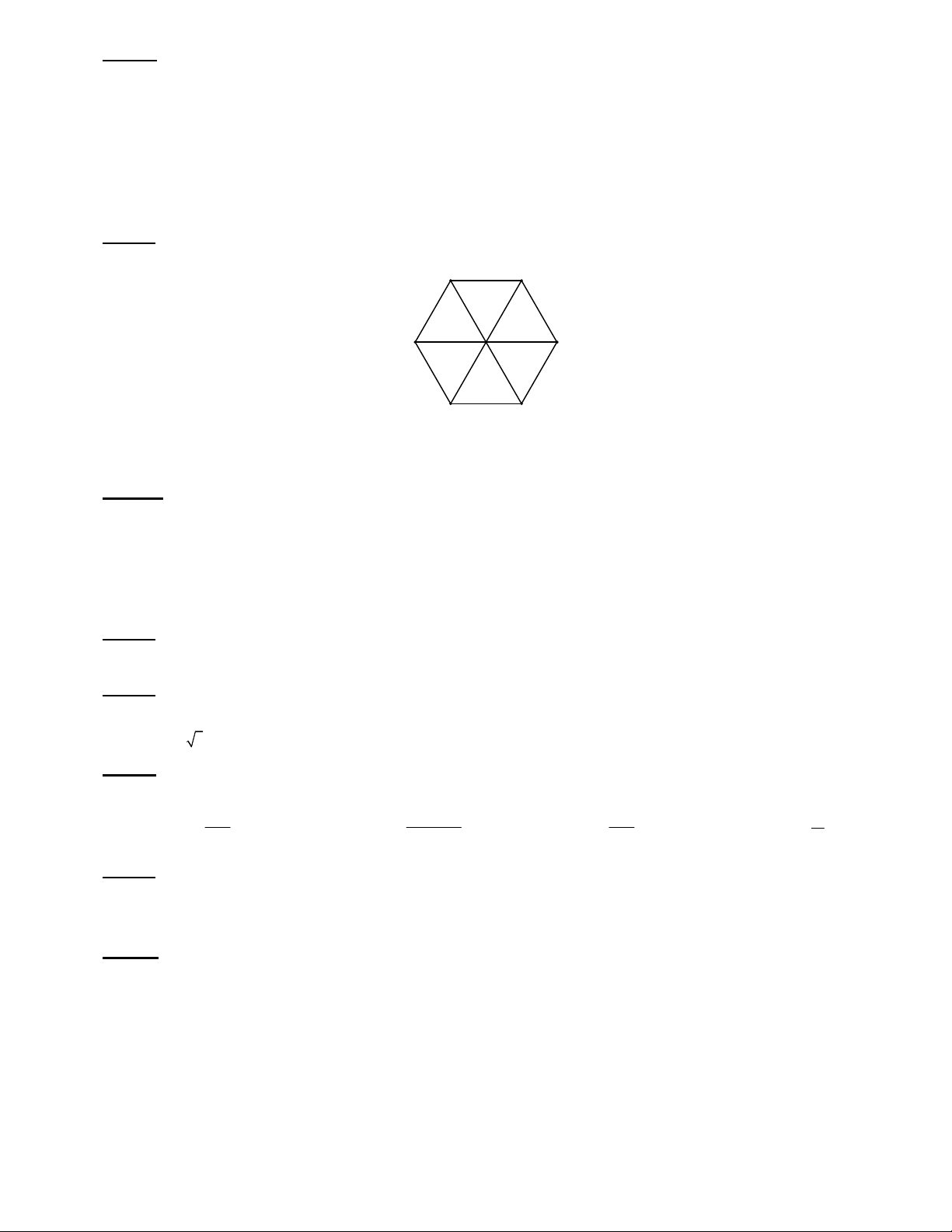
Câu 9. Cho , A B là hai tập hợp được minh họa như hình vẽ. Phần tô đen trong hình vẽ là tập hợp nào sau
đây?
A. A BÇ. B. \A B . C. \B A . D. A BÈ.
Câu 10. Mệnh đề phủ định của mệnh đề 2
:" , 5 4 0"Q x x x ฀ là mệnh đề
A. 2
" , 5 4 0"x x x ฀. B. 2
" , 5 4 0"x x x ฀.
C. 2
" , 5 4 0"x x x ฀. D. 2
" , 5 4 0"x x x ฀.
Câu 11. Cặp số
2;3 là nghiệm của bất phương trình nào dưới đây?
A. 2 8x y . B. 2 3 1x y . C. 3 2x y . D. 1x y .
Câu 12. Trên mặt phẳng Oxy , miền nghiệm của hệ bất phương trình
0
0
3 6
4
x
y
x y
x y
là miền tứ giác OABC
trong hình vẽ bên dưới.
Giá trị lớn nhất của biểu thức
, 2 2023F x y x y bằng
A. 2023. B. 2019 . C. 2022 . D. 2027 .
3
Câu 13. Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất
hai ẩn?
A.
3 5
2
x y
x y z
.
B. 2
3 2 10
12
x y
x y
.
C.
2 10
2xy
x y
x y
.
D.
3 7
2 5 12
x y
x y
.
Câu 14. Cho lục giác đều ABCDEF có tâm O. Có bao nhiêu vectơ bằng vec tơ EF
?
O
FE
D
CB
A
A. 5. B. 3. C. 2. D. 4.
Câu 15. Cho ba tập hợp
2;3;5;7 , 3 | , 4A B x x x ฀ và
2
| ( 1)(2 5 3) 0C x x x x ฀. Tìm
A B C
A.
2; 1;0;1;2;3;4;5;6;7 B. .
C.
3; 1;1. D.
2;3;5;7;0;6;9; 1;1.
Câu 16. Cho mệnh đề chứa biến P( ): " 3 0"x x Mệnh đề nào trong các mệnh đê dưới đây là sai?
A. (2).P B. (3).P C. (5).P D. (4)P
Câu 17. Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. “2 là một số lẻ”. B. “ 2024 chia hết cho 3”.
C. “3 là một số hữu tỷ”. D. “5 là một số nguyên tố”.
Câu 18. Cho tam giác ABC có ba cạnh lần lượt là a, b, c và có diện tích S. Bán kính đường tròn ngoại tiếp
của tam giác ABC bằng:
A. 4
abc
RS
. B. 4
a b c
RS
. C.
4S
Rabc
.
D.
.
S
Rp
.
Câu 19. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
A. 3 1x y . B. 1 0y . C. 3 2 1x y . D.
5 3 1x y xy .
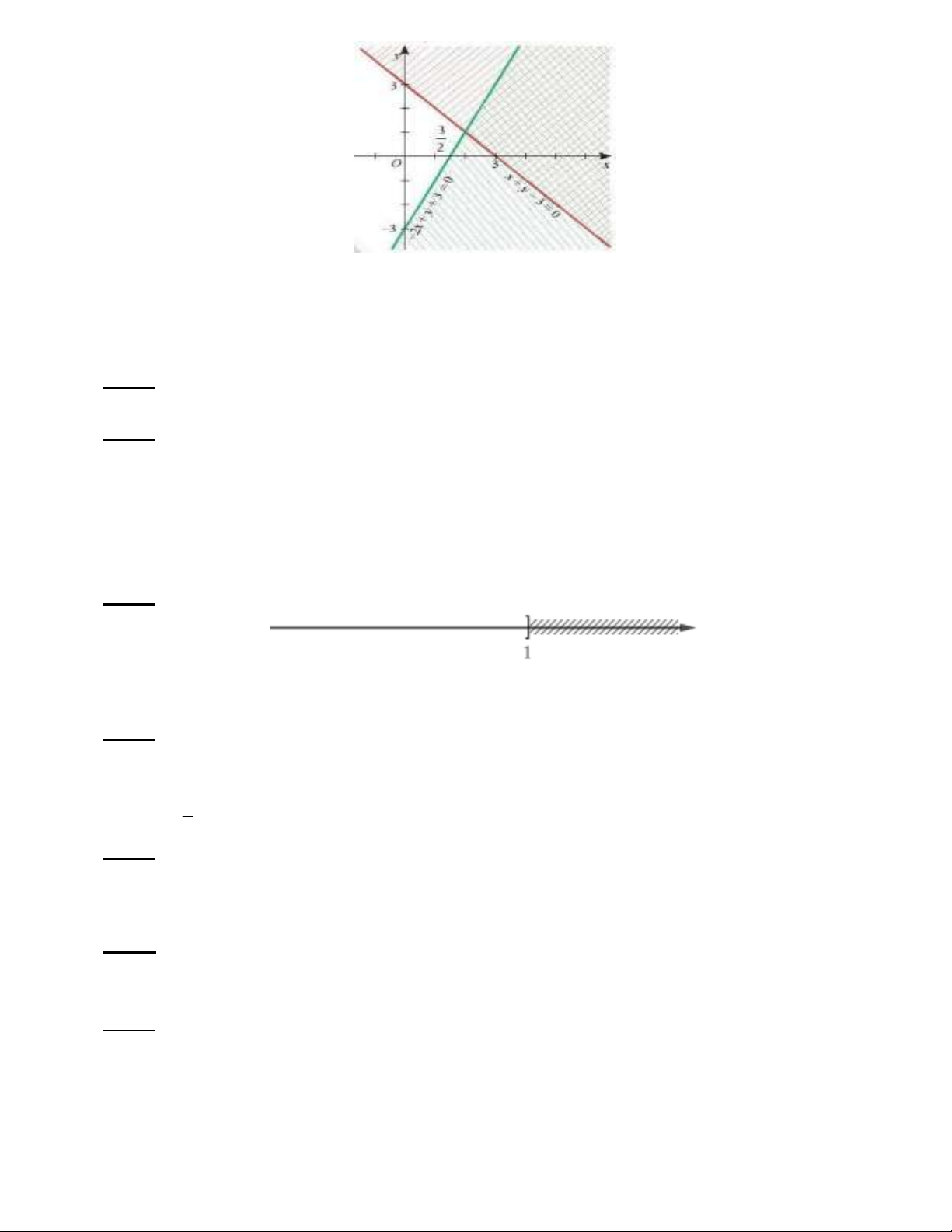
Câu 20. Miền không bị gạch chéo (kể cả bờ) trong hình bên dưới là biểu diễn miền nghiệm của hệ bất
phương trình nào?
4
A. 3 0
2 3 0
x y
x y
. B. 3 0
2 3 0
x y
x y
.
C. 3 0
2 3 0
x y
x y
. D. 3 0
2 3 0
x y
x y
.
Câu 21. Cho hình bình hành ABCD . Vectơ cùng hướng với vectơ AB
là
A. BA
. B. BC
. C. DC
. D. CD
.
Câu 22. Cặp số
; 1; 2x y là nghiệm của hệ bất phương trình nào sau đây?
A.
5
2 1
x y
x y
.
B.
3 1
2 0
x y
x y
.
C.
2
2 7
x y
x y
.
D.
10
2 4
x y
x y
.
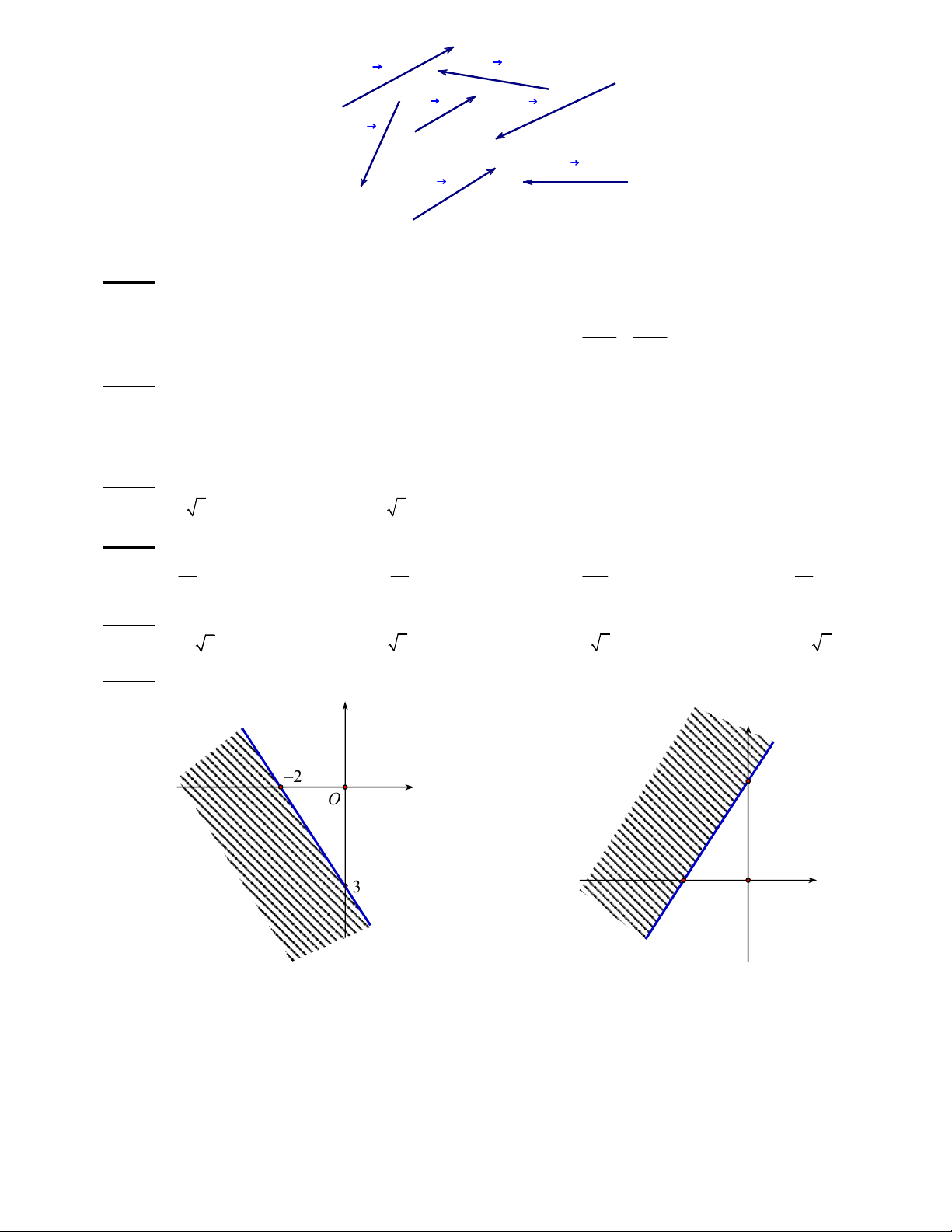
Câu 23. Tập hợp Mđược biểu diễn trên trục số trong hình bên dưới.
Tập hợp M tập hợp nào trong các tập hợp dưới đây?
A.
1; . B.
;1 . C.
;1 . D.
1; .
Câu 24. Cho tam giác ABC có các cạnh lần lượt là a, b, c. Khẳng định nào sau đây sai?
A.
1sin .
2
S bc A. B.
1sin .
2
S bc B. C.
1sin .
2
S ab C. D.
1sin .
2
S ac B.
Câu 25. Trong các đẳng thức sau,đẳng thức nào sai:
A. tan(90 ) cot
o
. B.
sin 90 cos
o
.
C. cot(90 ) tan
o
. D. cos(90 ) sin
o
.
Câu 26. Cho tam giác ABC có diện tích 2
24cm và nửa chu vi bằng 12cm . Tính bán kính đường tròn nội tiếp
của tam giác ABC.
A. 1 / 2 . B. 1. C. 2. D. 4.
Câu 27. Cho các vec tơ như hình vẽ bên dưới. Các vectơ cùng phương với vectơ a
là
5
v
u
e
d
c
b
a
A. ; ;c u e
. B. ; ;c u v
. C. e
. D. ;u c
.
Câu 28. Cho tam giác ABC có các cạnh lần lượt là a, b, c. Khẳng định nào sau đây đúng?
A. 2 2 2 .cosa b c bc A . B. 2 2 2 2 .cosa b c bc A .
C. .sin .sina A b B. D. sin sin
a b
B C
.
Câu 29. Cho
2;0;2;4;6 ; 3; 2; 1;0;1 .A B Khẳng định nào sau đây đúng?
A.
3; 2; 1;0;1;2;4;6 .A B . B.
2; 1;0;1;2;4;5;6 .A B .
C.
2;0 .A B . D.
3; 1;1;2;4;6 .A B .
Câu 30. Cho tam giác ABC có
฀
12, 150a A . Bán kính đường tròn ngoại tiếp của tam giác ABC bằng:
A. 6 2 . B. 3 2 . C. 12 . D. 6.
Câu 31. Cho tam giác ABC có ba cạnh 10; 6; 7a b c . Tính cos A
A.
29
40 . B.
12
25
. C.
113
140 . D.
5
28
.
Câu 32. Tính giá trị biểu thức 2sin135 6cos45 1A ?
A. 2 2. B. 2 2 1. C. 2 2 . D. 1 2 2.
Câu 33. Miền nghiệm (phần không bị gạch chéo) của bất phương trình 3 2 6 x y là
A. . B. .
Ox
y
2
3
Ox
2
3
y