Để giúp các bạn học sinh củng cố lại phần kiến thức đã học, biết cấu trúc ra đề thi như thế nào và xem bản thân mình mất bao nhiêu thời gian để hoàn thành đề thi này. Mời các bạn cùng tham khảo "Đề thi giữa học kì 1 môn Toán lớp 11 năm 2024-2025 có đáp án - Trường THPT Vĩnh Linh, Quảng Trị" dưới đây để có thêm tài liệu ôn thi. Chúc các bạn thi tốt!
AMBIENT/
Chủ đề:
Nội dung Text: Đề thi giữa học kì 1 môn Toán lớp 11 năm 2024-2025 có đáp án - Trường THPT Vĩnh Linh, Quảng Trị
- SỞ GD & ĐT QUẢNG TRỊ KIỂM TRA GIỮA KÌ 1 – NĂM HỌC 2024 - 2025
TRƯỜNG THPT VĨNH LINH MÔN TOÁN 11 CT 2018 - LỚP 11
Thời gian làm bài : 90 Phút; (Đề có 24 câu)
(Đề có 4 trang)
Họ tên : ..........................................................Lớp: ....... Số báo danh : ...................... Mã đề 998
PHẦN I (5.0 điểm): Học sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi học sinh chỉ chọn 01
phương án.
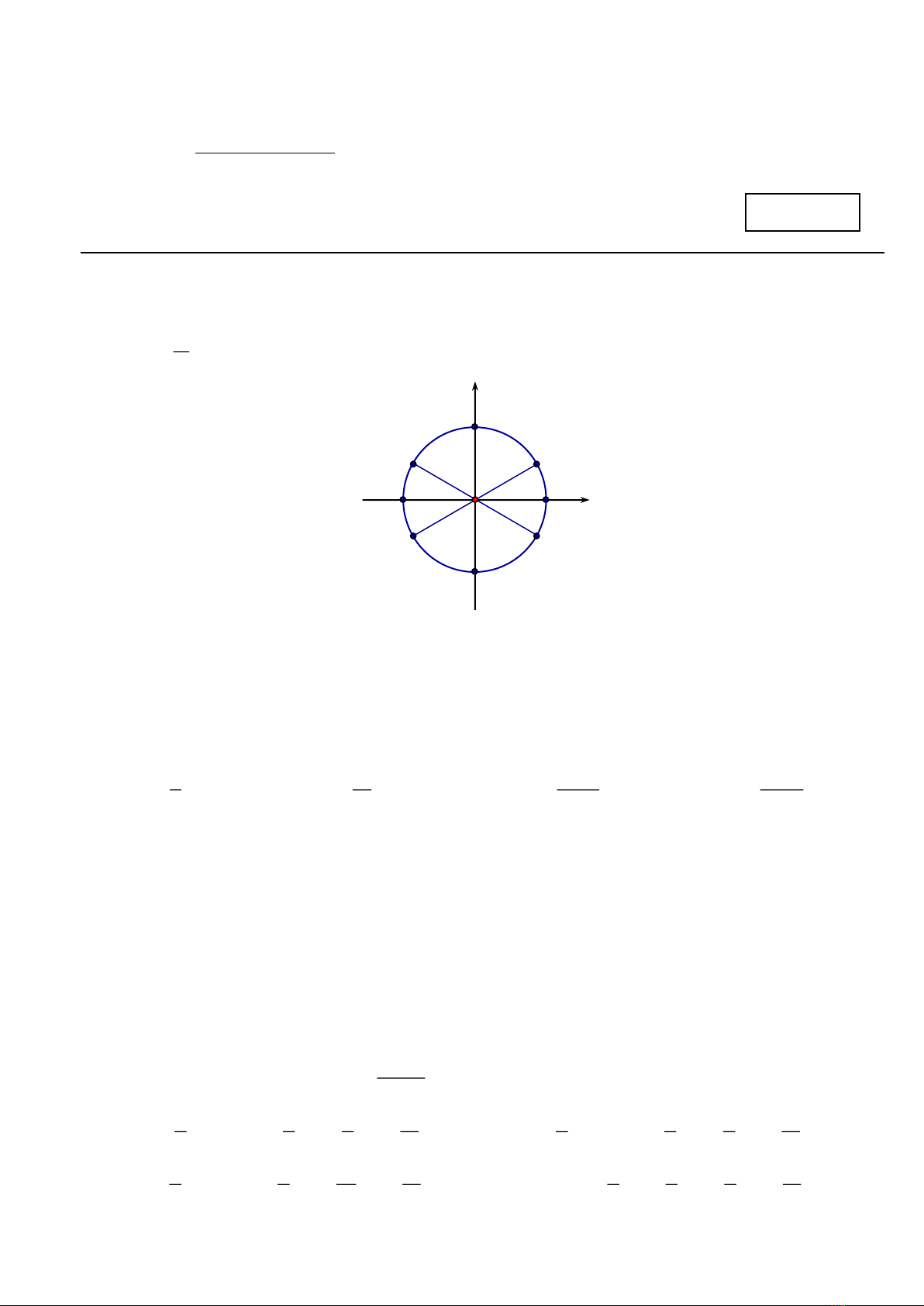
Câu 1: Cho đường tròn lượng giác như hình vẽ. Xác định điểm biểu diễn của góc lượng giác có
số đo là − ?
6
y
B
D C
A O A x
E F
B
A. F . B. C. C. E. D. D.
Câu 2: Cho cấp số cộng ( un ) có u1 = −7 và u2 = −2. Hãy tính u51 .
A. 244. B. 248. C. 243. D. 234.
Câu 3: Trong các dãy số ( un ) cho bởi số hạng tổng quát un sau, dãy số nào là dãy số tăng?
1 1 n+5 2n − 1
A. un = . B. un = . C. un =
. D. un = .
n 2n 3n + 1 n +1
u = 2
Câu 4: Cho cấp số cộng ( un ) được xác định bởi công thức: 1 ( n 2 ) . Giá trị của u3
un = un −1 − 3
bằng ?
A. u3 = −1. B. u3 = −3. C. u3 = 3. D. u3 = −4 .
Câu 5: Tìm khẳng định nào dưới đây đúng?
A. cos2a = 1 − 2sin a. B. sin 2a = 2sin 2 a. C. cos 2a = 2cos a − 1. D. cos 2a = 2cos a − 1
2
Câu 6: Dãy số nào sau đây là cấp số nhân?
A. 1; −1;1; −1;1 . B. 1;11;111;1111;11111 .
C. x;2 x;3x;4 x;5 x. với x 0 . D. 2;4;6;8;10.
n+3
Câu 7: Cho dãy số ( un ) , biết un = với n N * . Viết năm số hạng đầu của dãy số.
2n + 1
3 7 7 11 4 6 7 8
A. u1 = , u2 = 1, u3 = , u4 = , u5 = . B. u1 = , u2 = 1, u3 = , u4 = , u5 = .
4 6 9 8 3 7 9 11
4 7 9 8 3 5 7 8
C. u1 = , u2 = 1, u3 = , u4 = , u5 = . D. u1 = 1, u2 = , u3 = , u4 = , u5 = .
3 9 10 11 4 7 9 11
Mã đề 998
- 5
Câu 8: Họ nghiệm của phương trình co s x = co s là:
6
5 5
x = 6 + k 2 x = 6 + k 2
A. , k Z. B. , k Z.
x = 11 + k 2 x = + k 2
6
6
5 5
x= + k x= + k 2
6 6
C. , k Z. D. ,k Z .
x = − 5 + k x = − 5 + k 2
6
6
Câu 9: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số
liệu ghép nhóm sau:
Mệnh đề nào sau đây là sai?
A. Độ dài nhóm là 20. B. Số học sinh là 42.
C. Cỡ mẫu là 5. D. Nhóm chứa mod là [40;60) .
2
Câu 10: Cho góc lượng giác = . Khẳng định nào sau đây đúng?
3
1 − 2 − 3 −1
A. cos = . B. sin = . C. cos = . D. cos = .
2 2 2 2
Câu 11: Trong các công thức sau, công thức nào đúng?
A. sin ( a − b ) = sin a.cos b − cos a.sin b. B. sin ( a + b ) = sin a.cos b − cos a.sin b.
C. cos ( a + b ) = cos a.cos b + sin a.sin b. D. cos ( a − b ) = cos a.cos b − sin a.sin b.
Câu 12: Tính giá trị biểu thức P = sin .co s .co s .co s ?
24 24 12 6
3 3 1 1
A. P = . B. P = . C. P = . D. P = .
8 16 16 8
Câu 13: Đổi sang Rad góc lượng giác có số đo 50 ?
0
5 5 5
A. . B. . C. . D. .
18 6 5 18
Câu 14: Tìm hiểu thời gian xem tivi trong tuần (đơn vị: giờ) của một số học sinh thu được kết
quả sau:
Nhóm chứa mốt là nhóm nào?
A. 20; 25) . B. 15;20 ) . C. 16. D. 5;10 ) .
1
Câu 15: Phương trình sin x = có nghiệm là :
2
Mã đề 998
-
x = + k 2 x = + k
6 6
A. , k Z. B. , k Z.
x = − + k 2 x = 5 + k
6
6
x = 6 + k 2 x = 3 + k 2
C. , k Z. D. , k Z.
x = 5 + k 2 x = − + k 2
6
3
2
Câu 16: Cho cấp số nhân (u n ) có số hạng đầu u1 = và công bội q = 3 . Tìm u 4 .
3
20 16
A. u4 = 18 . B. u4 = . C. u4 = . D. u4 = 16.
3 3
Câu 17: Khảo sát thời gian chơi thể thao của một số học sinh thu được kết quả sau:
Tính mốt của mẫu số liệu trên ?
A. 10,29 . B. 11 . C. 11,875 . D. 11,1.
Câu 18: Khảo sát số giấy vụn ủng hộ của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm như sau:
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. 6; 8 ) . B. 4; 6 ) . C. 8;10 ) . D. 2; 4 ) .
Câu 19: Khẳng định nào dưới đây là sai?
A. Hàm số y = cot x là hàm số chẳn. B. Hàm số y = sin x là hàm số lẻ.
C. Hàm số y = cos x là hàm số chẳn. D. Hàm số y = tan x là hàm số lẻ.
Câu 20: Tìm khẳng định đúng?
A. Hàm số y = tan x là hàm số tuần hoàn với chu kì 2.
B. Hàm số y = sin x là hàm số tuần hoàn với chu kì .
C. Hàm số y = cos x là hàm số tuần hoàn với chu kì .
D. Hàm số y = cot x là hàm số tuần hoàn với chu kì .
PHẦN II (2.0 điểm): Học sinh trả lời từ câu 21 đến câu 22. Trong mỗi ý a), b), c), d) ở mỗi
câu, học sinh chọn đúng hoặc sai.
Câu 21: Cho góc lượng giác x, x . Ta có:
2
2 5 5
a) Với tan x = − khi đó co t x = .
5 2
b) sin x 0.
c) cos ( + x ) 0.
d) Giá trị lớn nhất của hàm số y = 3co s x + 7 trên đoạn ; bằng 7 .
2
Mã đề 998
- 1 3
Câu 22: Cho cấp số cộng ( un ) có số hạng đầu u1 = − , công sai d = . Ta có:
2 2
a) u7 + u25 = 44 .
3625
b) Tổng 50 số hạng đầu của cấp số cộng là S50 = .
2
c) Số là số hạng thứ 100 của dãy cấp số cộng.
3
d) Số hạng tổng quát của dãy là un = n - 2 .
2
PHẦN III (3.0 điểm): Học sinh trả lời từ câu 23 đến câu 24
Câu 23(1,5 điểm).
a.Giải phương trình : cos7 x + sin3x = 0 .
5 3
b. Tính giá trị cos , biết sin = − và .
4 2
c. Cho biết d = m − n cos (t − 60) trong đó m,n là các số thực cho trước, n 0 là
168
công thức dùng để tính số giờ d có ánh sáng mặt trời của một thành phố X ở vĩ độ 400 bắc trong
ngày thứ t của năm không nhuận với 0 t 365, t N . Biết số giờ ánh sáng mặt trời chiếu nhiều
nhất trong ngày là 12 giờ và ít nhất trong ngày là 8 giờ. Hỏi ngày thứ mấy của năm có số giờ
ánh sáng mặt trời là 9 giờ ?
Câu 24(1,5 điểm).
a. Một công ty tuyển dụng nhân viên với hợp đồng 10 năm và nhân viên được chọn trả
lương theo một trong hai phương án sau :
Phương án 1 : Lương tháng khởi điểm là 8 triệu đồng và cứ sau mỗi quý, lương tháng sẽ tăng
thêm 600 ngàn đồng .
Phương án 2 : Lương tháng khởi điểm là 8 triệu đồng và cứ sau mỗi quý, lương tháng sẽ tăng
thêm 5% .
Với phương án nào thì tổng lương nhận được của nhân viên sau 10 năm làm việc sẽ nhiều hơn ?
(lưu ý : 1 quý bằng 3 tháng)
b. Khảo sát thời gian nghỉ trưa (tính theo phút) của một số người thu được mẫu số liệu
ghép nhóm sau:
Tính số trung vị của mẫu số liệu ghép nhóm trên ?
c. Với mong muốn người tiêu dùng tiết kiệm điện, một công ty điện lực bán điện sinh
hoạt cho người dùng với giá điện tính theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm
10 số điện (1 số điện bằng 1kWh ); bậc 1 từ số điện thứ 1 đến số điện thứ 10, bậc 2 từ số điện
thứ 11 đến số điện thứ 20, bậc 3 từ số điện thứ 21 đến số điện thứ 30,.... Giá của mỗi số điện ở
bậc 1 là 1500 đồng/số, giá của mỗi số ở bậc thứ n , (n N , n 2) tăng 2,5% so với giá của mỗi
số điện ở bậc thứ n − 1 . Biết rằng trong tháng 1 năm 2024 gia đình cô A sử dụng hết 345 số
điện, hỏỉ gia đình cô A phải đóng bao nhiêu tiền? (làm tròn kết quả đến hàng đơn vị).
------ HẾT ------
Mã đề 998
- Phần đáp án câu trắc nghiệm:
998
1 A
2 C
3 D
4 D
5 C
6 A
7 B
8 D
9 C
10 D
11 A
12 B
13 D
14 D
15 C
16 A
17 C
18 B
19 A
20 D
Phần đáp án câu trắc nghiệm đúng, sai:
998
21 A- S; B- Đ; C- S; D- Đ;
22 A- Đ; B- Đ; C- S; D- Đ;
ĐÁP ÁN TỰ LUẬN( 3 điểm )
Câu Nội dung Điểm
0.25
cos 7 x = − sin 3 x cos 7 x = cos + 3 x
2
23a(VD)
7 x = 2 + 3 x + k 2 4 x = 2 + k 2 x = 8 + k 2
0.25
,k Z
7 x = − − 3 x + k 2 10 x = − + k 2 x = − + k
2
2
20 5
5 3
sin = − và
4 2
23b(VD) 0.25
11
Vì sin + cos = 1 cos =
2 2 2
16
3 11
do cos = −
2 4 0,25
Số giờ ánh sáng mặt trời chiếu cao nhất là m + n khi
cos (t − 60) = −1 và thấp nhất bằng m−n khi
168
Mã đề 998
- m + n = 12 m = 10
23c cos (t − 60) = 1 . Theo giả thiết, ta có: 0,25
168 m − n = 8 n = 2.
Từ trên ta có công thức: d (t ) = 10 − 2cos (t − 60) . Do có số giờ
168
ánh sáng mặt trời chiếu là 9 giờ nên:
1
10 − 2cos (t − 60) = 9 cos (t − 60) =
186 186 2 0,25
168 (t − 60) = 3 + k 2 t = 116 + k 336
(k ) (k ).
(t − 60) = − + k 2 t = 4 + k .336
168
3
Ứng với 3 ngày trong năm là : ngày thứ 4, ngày thứ 116 và ngày thứ
340.
Phương án 1: Là cấp số cộng có u1 = 24.106 , d = 1,8.106
Tổng tiền nhận được trong 10 năm(40 quý) là:
40
S40 = 2.24.106 + ( 40 − 1) .1,8.106 = 2364.106
2 0,25
24a
Phương án 2 : Là cấp số nhân có u1 = 24.106 , q = (1 + 5%) = 1,05
Tổng tiền nhận được trong 10 năm(40 quý) là:
6 1 − (1,05 )
40
S20 = 24.10 = 2.899.194.582 0,25
1 − 1,05
Vậy khi làm hợp đồng trong 10 năm nên chọn phương án 2
Trung vị (Me)
Cở mẫu số liệu n = 50.
n + 1 50 + 1
Ta có = = 25,5
2 2 0.25
Suy ra trung vị của mẫu số liệu gốc là
24b
x + x26
M e = 25 , x25 ; x26 40;60 ) = p = 2
2
(Tính được cở mẫu và chỉ được số trung vị thuộc nhóm : cho 0,25 đ)
Áp dụng công thức
n 50
− (m1 + m2 + ... + m p −1 ) − 12 490
0.25
M e = ap + 2 .(a p +1 − a p ) = 40 + 2 .20 =
mp 18 9
Ta thấy 345 số gồm có 34 bậc từ bậc 1 đến bậc 34 và 5 số ở bậc 35
Số tiền phải trả ở bậc 1 là : u1 = 10.1500 = 15000
24c Số tiền phải trả ở bậc 2 là :
u2 = u1 + u1.2,5% = u1 (1 + 2,5%) = 15000(1 + 2,5%)
Số tiền phải trả ở bậc 3 là : 0.25
Mã đề 998
- u3 = u2 + u2 .2,5% = u2 (1 + 2,5%) = 15000(1 + 2,5%) 2
….
Số tiền phải trả ở bậc 34 là :
u34 = 15000(1 + 2,5%)33
Số tiền phải trả cho 5 số ở bậc 35 là: u35 = 1500.5(1 + 2,5%)34
Vậy dãy số là cấp số nhân có u1 = 15000; q = 1 + 2,5%
0.25
1 − (1 + 2,5%)34
S = 15000. + 1500.5(1 + 2,5%)34 = 806558,1956
1 − (1 + 2,5%)
Vậy số tiền phải trả trong tháng 1 là : 806558 đồng
Mã đề 998
Thêm vào BST
Báo xấu
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
