PHÒNG GD&ĐT YÊN LẠC
TRƯỜNG THCS YÊN PHƯƠNG
ĐỀ KSCL GIỮA KÌ 1
NĂM HỌC 2022-2023
Môn : Toán 8
(Thời gian làm bài 90 phút)
A.TRẮC NGHIỆM (2 điểm) :
Chọn một chữ cái A, B, C hoặc D trước mỗi phương án em cho là đúng, ghi vào tờ giấy
thi :
Câu 1. Kết quả của phép nhân 3x(x – 2) là:
A. 3x2 + 6x B. 2x2 - 6x C. 3x2 - 6x D. 3x2 - 2x
Câu 2. Kết quả của phép nhân (x +3)(x - 2) là:
A. x2 +2x +6 B. x2 + 3x - 6 C. x2 + x + 6 D. x2 + x - 6
Câu 3. Giá trị của biểu thức (x – 2)(x2 + 2x + 4) tại x = 2 là:
A. 0 B. - 16 C. - 14 D. 2
Câu 4. Cho điểm A đối xứng với điểm B qua O, điểm C đối xứng với điểm D qua O. Trong các
nhận xét sau, nhận xét nào không đúng?
A. AC = BD B. BC = AD C. AB = CD D. BC // AD
B. TỰ LUẬN (8 điểm)
Câu 5 (2 điểm)Viết các đa thức sau dưới dạng bình phương của một tổng hay một hiêu.
a) y2 + 2y + 1 b) 9x2 +y2 – 6xy
c) 25a2 +4b2 +20ab d) x2 – x +
Câu 6 (2,5 điểm )Phân tích các đa thức sau thành nhân tử.
a) 14x2y – 21xy2 + 28x2y2b) 27x3–
c) 3x2 – 3xy –5x + 5y d) x2+ 7x + 12
e) x3 – 7x – 6
Câu 7 (1 điểm )Tìm x biết :
a) x(x – 2) + x – 2 = 0 b) 5x(x – 3) – x + 3 = 0
Câu 8 (1 điểm)Tìm x,y,z thỏa mãn9x2 + y2 + 2z2 – 18x + 4z – 6y + 20 = 0.
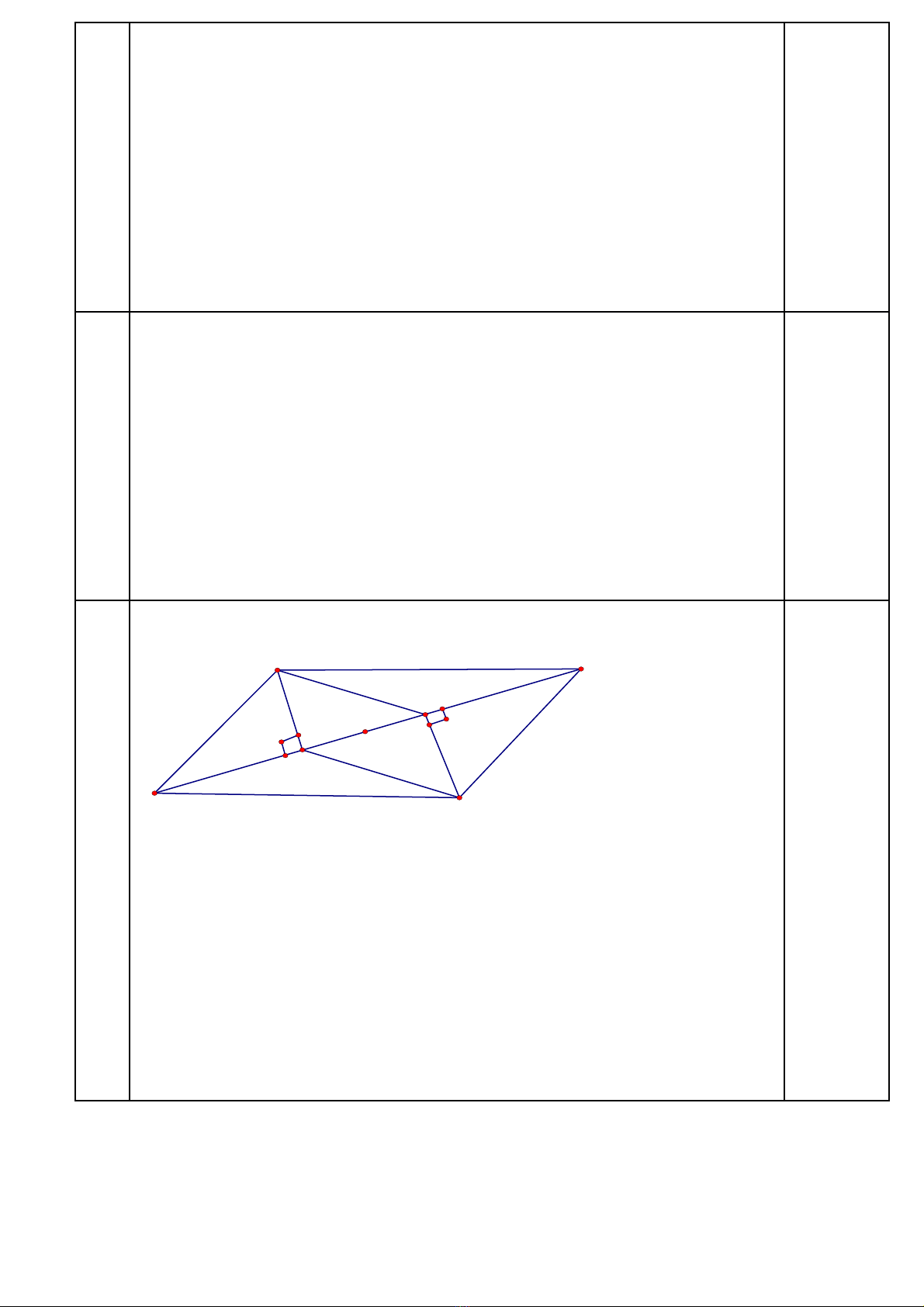
Câu 9(1,5 điểm) Cho hình bình hành MNPQ. Từ M, P kẻ đường vuông góc với NQ lần
lượt tại A và C.
a) Chứng minh rằng tứ giác MAPC là hình bình hành.
b) Gọi I là trung điểm của AC. Chứng minh rằng ba điểm M, I, P thẳng hàng
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ KSCL GIỮA KÌ 1 NĂM HỌC 2022 - 2023
Môn: Toán 8
A. Trắc nghiệm(2điểm). Mỗi câu trả lời đúng được 0,5 điểm
Câu 1 2 3 4
Đáp án C D A C
B. Tự luận (8điểm)
Câu Nội dung Điểm
5 a) y2 + 2y + 1 = ( y + 1)2
b) 9x2 +y2 – 6xy = (3x)2 – 2.3xy + y2= (3x – y)2
c) 25a2 + 4b2 + 20ab = (5a)2 + 2.5 2ab + (2b)2 = (5a + 2b)2
d) x2 – x + = x2 – 2.x + ()2 = (x –)2
0,5
0,5
0,5
0,5
6
a) 14x2y – 21xy2 + 28x2y2 = 7xy( 2x – 3y + 4xy)
b) 27x3 – = (3x)3 – ()3 =( 3x –)(9x2 + x +
c) 3x2 – 3xy –5x + 5y = (3x2 – 3xy) – (5x +5y)
= 3x(x – y) – 5(x – y) = (x – y)(3x – 5)
d) x2+ 7x + 12 = x2 + 3x + 4x + 12 = (x2 + 3x) + (4x +12)
= x(x + 3) + 4(x + 3) = (x + 3)( x + 4 )
e) x3 – 7x – 6 = x3 – 4x – 3x – 6 = x(x2 – 22) – 3(x + 2)
= x(x + 2)(x – 2) – 3(x + 2)= (x + 2)(x2 – 2x – 3)
= (x + 2)(x2 – 1 – 2x – 2)= (x + 2) [(x – 1)(x + 1) – 2(x + 1)]
= (x + 2)(x + 1)(x – 3)
0,5
0,5
0,5
0,5
0,5
7
a) x(x–2) + x –2 = 0
x(x – 2) + (x – 2) = 0
(x – 2)(x + 1) = 0
Vậy x – 2 = 0 hoặc x + 1 = 0 hay x = 2 hoặc x = -1
b) 5x(x –3) – x +3 = 0
5x(x –3) – ( x – 3) = 0
( x – 3)(5x – 1) = 0
Vậy x – 3 = 0 hoặc 5x – 1 = 0 hay x = 3 hoặc x = 1/5
0,5
0,5
8
9x2 + y2 + 2z2 – 18x + 4z – 6y + 20 = 0
(9x2 – 18x + 9) + (y2 – 6y + 9) + 2(z2 + 2z + 1) = 0
9(x – 1)2 + (y – 3)2 + 2 (z + 1)2 = 0 (*)
Do :
Nên : (*) x = 1; y = 3; z = -1
Vậy (x,y,z) = (1, 3, -1).
1
9
Vẽ hình đúng
I
C
A
Q
P
N
M
a) Tứ giác MAPC có MA NQ và PC NQ => MA // PC (1)
Xét MAQ vàNPC có : = = 900
MQ = NP (MNPQ là hình bình hành)
= (2 góc so le trong do MQ // NP)
Suy ra MAQ =PCN( cạnh huyền - góc nhọn)
=> MA = PC (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra tứ giác MAPC là hình bình hành
b) Xét hình bình hành MAPC, trung điểm I của đường chéo AC cũng là
trung điểm của đường chéo MP ( tính chất đường chéo hình bình hành).
Do đó ba điểm M, I , P thẳng hàng
0,25
0,5
0,25
0,5