PHÒNG GD&ĐT ĐẠI LỘC
TRƯỜNG THCS VÕ THỊ SÁU ĐỀ KIỂM TRA GIỮA HỌC KÌ I. NĂM HỌC 2022- 2023
MÔN TOÁN - LỚP 9 (thời gian 60 phút)
(Kèm theo Công văn số 1749/SGDĐT-GDTrH ngày 13/10/2020 của Sở GDĐT Quảng Nam)
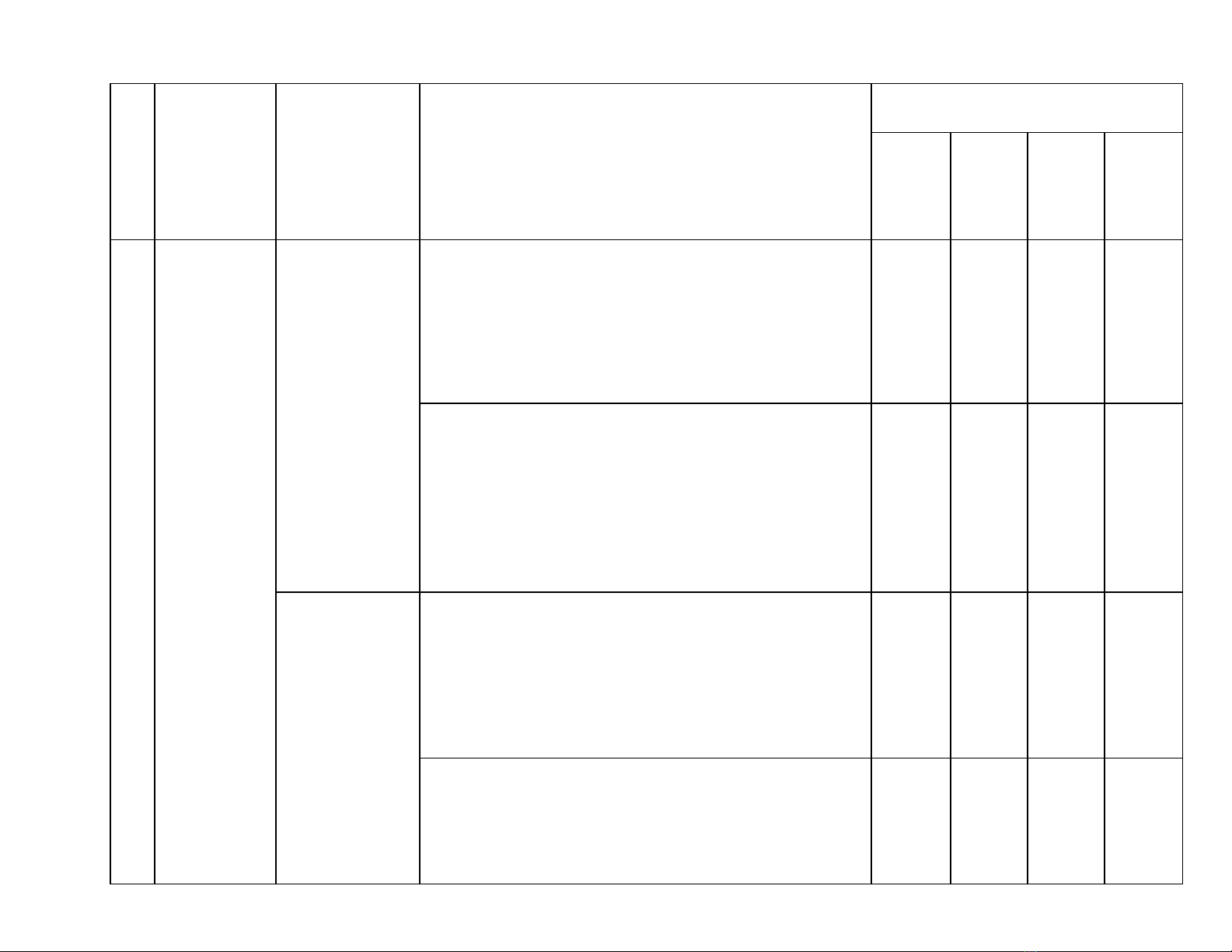
1. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I MÔN TOÁN – LỚP 9
TT
(1)
Chương/Chủ
đề
(2)
Nội dung/đơn vị kiến
thức
(3)
Mức độ đánh giá
(4-11)
Tng %
điểm
(12)
Nhn biết
Thông hiểu
Vn dng cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1
Căn thức
(18 tiết)
Căn bậc hai và căn bậc
ba của số thực
3
(0,75)
2
(1,0)
4
(1,0)
1
(0,75)
35%
Căn thức bậc hai và
căn thức bậc ba của
biểu thức đại số
1
(0,25)
2
(1,25)
15%
2
Hệ thức
lượng trong
tam giác
vuông
(17 tiết)
Tỉ số lượng giác của
góc nhọn. Một số hệ
thức về cạnh và góc
trong tam giác vuông
2
(0,5)
1
(1,0)
2
(0,5)
1
(0,75)
1
(0,75)
1
(1,0)
50%
Tng số câu
6
3
6
2
3
1
21
Tỉ lệ %
30-40%
30-40%
10%
100%
Tỉ lệ chung
70%
30%
100%
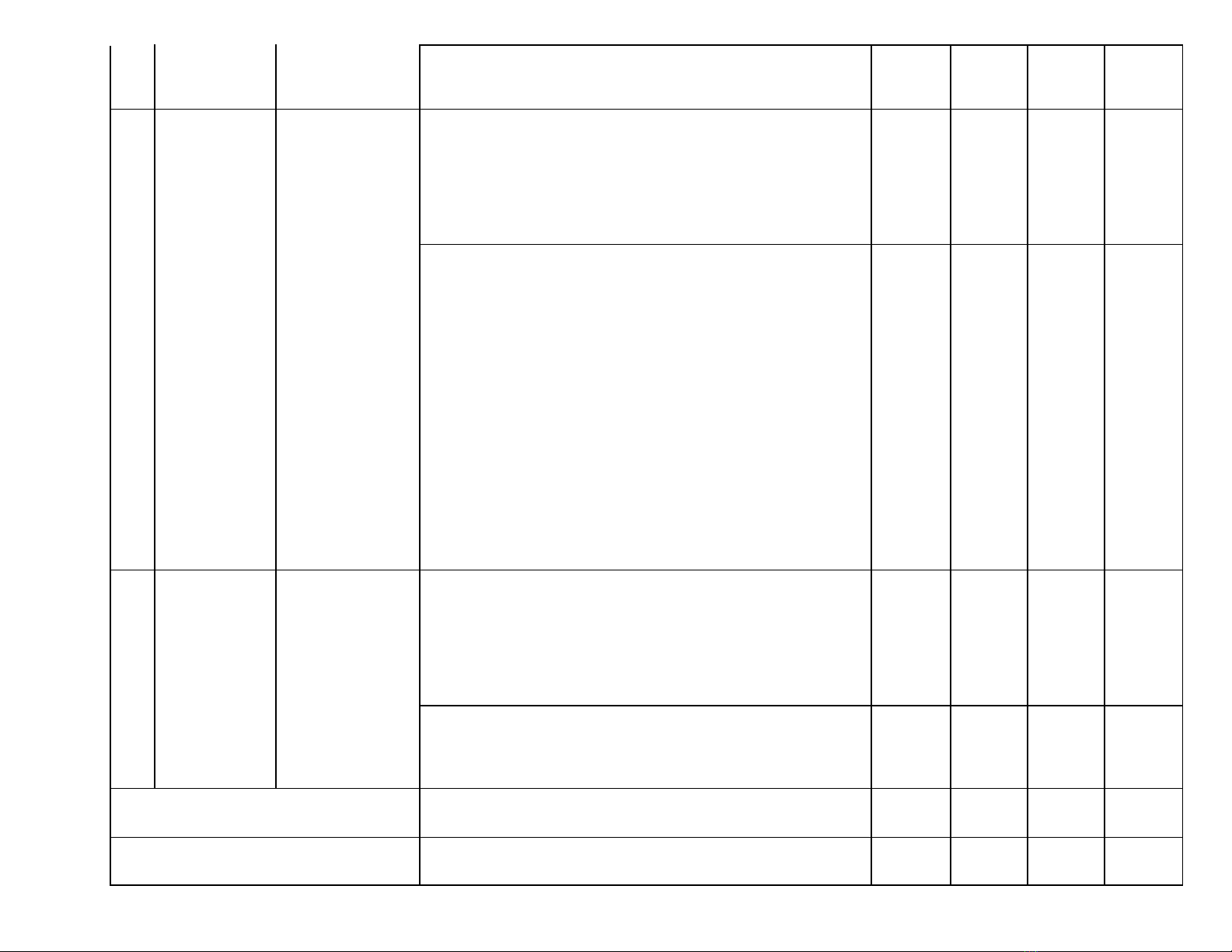
2. BẢNG ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TOÁN – LỚP 9
TT
Chương/
Chủ đề
Nội dung/Đơn
vị kiến thức
Mức độ đánh giá
Số câu hỏi theo mức độ nhn thức
Nhn
biêt
Thông
hiểu
Vn
dng
Vn
dng
cao
1
Căn thức
(18 tiết)
Căn bậc hai và
căn bậc ba của
số thực
Nhn bit :
- Nhn bit được khái niệm về căn bc hai của số thực
không âm, căn bc ba của một số thực.
5
(TN1,
TN2,
TN3,
TL13)
Thông hiểu:
- Tính được giá trị (đúng hoặc gần đúng) căn bc hai, căn
bc ba của một số hữu tỉ bằng máy tính cầm tay.
5
(TN5,
TN6,
TN7,
TN8,
TL14)
Căn thức bậc
hai và căn
thức bậc ba
của biểu thức
đại số
Nhn bit:
- Nhn bit được khái niệm về căn thức bc hai và căn
thức bc ba của một biểu thức đại số.
1
(TN4)
Vn dụng:
- Thực hiện được một số phép tính đơn giản về căn bc
hai của số thực không âm (căn bc hai của một bình
phương, căn bc hai của một tích, căn bc hai của một
2
(TL15)
thương, đưa thừa số ra ngoài dấu căn bc hai, đưa thừa số
vào trong dấu căn bc hai).
2
Hệ thức
lượng trong
tam giác
vuông
(17 tiết)
Tỉ số lượng
giác của góc
nhọn. Một số
hệ thức về
cạnh và góc
trong tam giác
vuông
Nhn bit:
- Nhn bit được các giá trị sin (sine), côsin (cosine), tang
(tangent), côtang (cotangent) của góc nhọn.
3
(TN9,
TN10,
TL16a)
Thông hiểu:
– Giải thích được tỉ số lượng giác của các góc nhọn đặc
biệt (góc 30o, 45o, 60o) và của hai góc phụ nhau.
– Giải thích được một số hệ thức về cạnh và góc trong tam
giác vuông (cạnh góc vuông bằng cạnh huyền nhân với
sin góc đối hoặc nhân với côsin góc kề; cạnh góc vuông
bằng cạnh góc vuông kia nhân với tang góc đối hoặc
nhân với côtang góc kề).
– Tính được giá trị (đúng hoặc gần đúng) tỉ số lượng giác
của góc nhọn bằng máy tính cầm tay.
3
(TN11,
TN12,
TL16b)
Vn dụng:
- Giải quyt được một số vấn đề thực tiễn gắn với tỉ số
lượng giác của góc nhọn (ví dụ: Tính độ dài đoạn thẳng,
độ lớn góc và áp dụng giải tam giác vuông,...).
1
(TL16c)
Vn dụng cao:
- Ứng dụng thực t các tỉ số lượng giác của góc nhọn.
1
(TL17)
Tng số câu
9
8
3
1
Tỉ lệ %
40%
30%
20%
10%
Tỉ lệ chung
70%
30%
Ghi chú:
- Hình vẽ được xem là 1 câu ở mức thông hiểu..
- Các bài tp kiểm tra việc nhớ các kin thức (công thức, quy tắc,...) được xem ở mức nhn bit.
- Các bài tp có tính áp dụng kin thức (theo quy tắc, thut toán quen thuộc, tương tự SGK...) được xem ở mức thông hiểu.
- Các bài tp cần sự liên kt các kin thức được xem ở mức vn dụng thấp; có sự linh hoạt, sáng tạo được xem ở mức vn dụng
cao.
ĐỀ CHÍNH THỨC
PHÒNG GD&ĐT ĐẠI LỘC
TRƯỜNG THCS VÕ THỊ SÁU
KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2022 – 2023
Môn: TOÁN – Lớp 9
Thời gian: 60 phút (không kể thời gian giao đề)
(Đề kiểm tra có 02 trang)
Phần I (3,0 điểm): Chọn câu trả lời đúng nhất cho mỗi câu hỏi sau ri ghi vào giấy làm bài. V
d: Câu 1 chọn câu trả lời A th ghi 1-A.
Câu 1: Căn bc hai số học của 4 là
A. –2. B. 2. C. 4. D.
2.
Câu 2: Căn bc ba của –64 là
A. 2. B. 4. C. –4. D. –2.
Câu 3: Chọn căn thức bc hai trong các biểu thức sau:
A.
3.
B.
2
25 −x
. C.
( )
2
1x−
. D.
25
7
x
x
+
−
.
Câu 4: Khẳng định nào dưới đây là đúng?
A.
327 9=
. B.
327 3=−
. C.
327 3=
. D.
327 9=−
.
Câu 5: Giá trị của biểu thức
5x−
tại
149x=
là
A. 12. B. –12. C. 12,2. D.
149
.
Câu 6: Kt quả của
( )
2
6
−
bằng
A. –6. B. 36. C. 6. D. –36.
Câu 7: Kt quả của phép tính
125 81 16+−
là
A. 130. B. 125. C. 190. D. 138.
Câu 8: Kt quả của phép tính
397−
(làm tròn đn chữ số thp phân thứ hai) là
A. – 4,55. B. – 4,60. C. 4,59. D. – 4,59.
Câu 9: Tỉ số giữa cạnh kề và cạnh huyền của tam giác vuông có góc nhọn
được gọi là:
A.
sin
. B.
cot
. C.
tan
. D.
cos
.
Câu 10: Cho hình sau, sinB bằng:
A.
AH
AB
B.
cosC
.
C.
AC
BC
. D. A, B, C đều đúng.