TRƯỜNG THCS LÊ QUÝ ĐÔN
TỔ KHOA HỌC TỰ NHIÊN
ĐỀ CHÍNH THỨC
KIỂM TRA GIỮA KỲ I - NĂM HỌC 2024-2025
Môn: Toán – Lớp 9
Thời gian: 90 phút (Không kể thời gian giao đề)
( Đề gồm có 2 trang )
I. TRẮC NGHIỆM (3,0 điểm): Hãy chọn một phương án trả lời đúng cho mỗi câu sau rô)i
ghi va)o giấy la)m ba)i.
Câu 1 [NB]: Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn?
A. . B. .C. .D. .
Câu 2 [NB]: Trong các cặp số sau, cặp số nào là nghiệm của phương trình ?
A. . B. . C. . D. .
Câu 3 [NB]: Hệ phương trình nào sau đây không phải là hệ hai phương trình bậc nhất hai
ẩn?
A. . B. . C. . D. .
Câu 4 [NB]: Cặp số nào sau đây là nghiệm của hệ phương trình
A. (2 ; 1). B. (-2 ; 1). C. (3 ; - 1). D. (-1, 3) .
Câu 5 [NB]: Hệ phương trình nào sau đây vô nghiệm ?
A. B. C. D.
Câu 6 [NB]: Hệ phương trình
A. Có vô số nghiệm B. Vô nghiệm.
C. Có nghiệm duy nhất. D. có hai nghiệm.
Câu 7 [NB]: Nếu thì
A. . B. . C. . D..
Câu 8 [NB]: Cho biết , khẳng định nào sau đây là sai?
A. . B. . C. . D. .
Câu 9 [NB]: Tam giác ABC vuông tại A, tanB bằng
A. B. C. D.
Câu 10 [NB]: Cho tam giác ABC vuông tại A. Hệ thức nào sau đây là đúng:
A. AB = BC. cosC . B. AC = BC . sin B.
C. AB = AC . tanB. D. AC = AB.cotB.
Câu 11[NB]: Giá trị của biểu thức bằng
A. -1. B. 0. C. 1. D. 2.
Câu 12 [NB]: cos 300 bằng
A..B. . C. . D. .
II. TỰ LUẬN (7,0 điểm):
Bài 1: (TH) (2,0 điểm)
a) Giải phương trình (x + 3) (x - 8) = 0
b) Chứng minh < .
Bài 2: a) (VD) (1,0 điểm) Giải hệ phương trình: .
b) (VD) (1,0 điểm) Giải bài toán bằng cách lập hệ phương trình
Tìm số tự nhiên n có hai chữ số, biết rằng tổng của hai chữ số đó bằng 10, và nếu viết
hai chữ số đó theo thứ tự ngược lại thì được một số có hai chữ số nhỏ hơn n là 18 đơn vị.
Bài 3: (2,0 điểm)
a) (NB) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 450 :
Cot650; sin550; cos530; tan820.
b) (TH) Giải tam giác ABC vuông tại A biết BC = 10cm ; = 600.
Bài 4 (VD) (1,0 điểm):
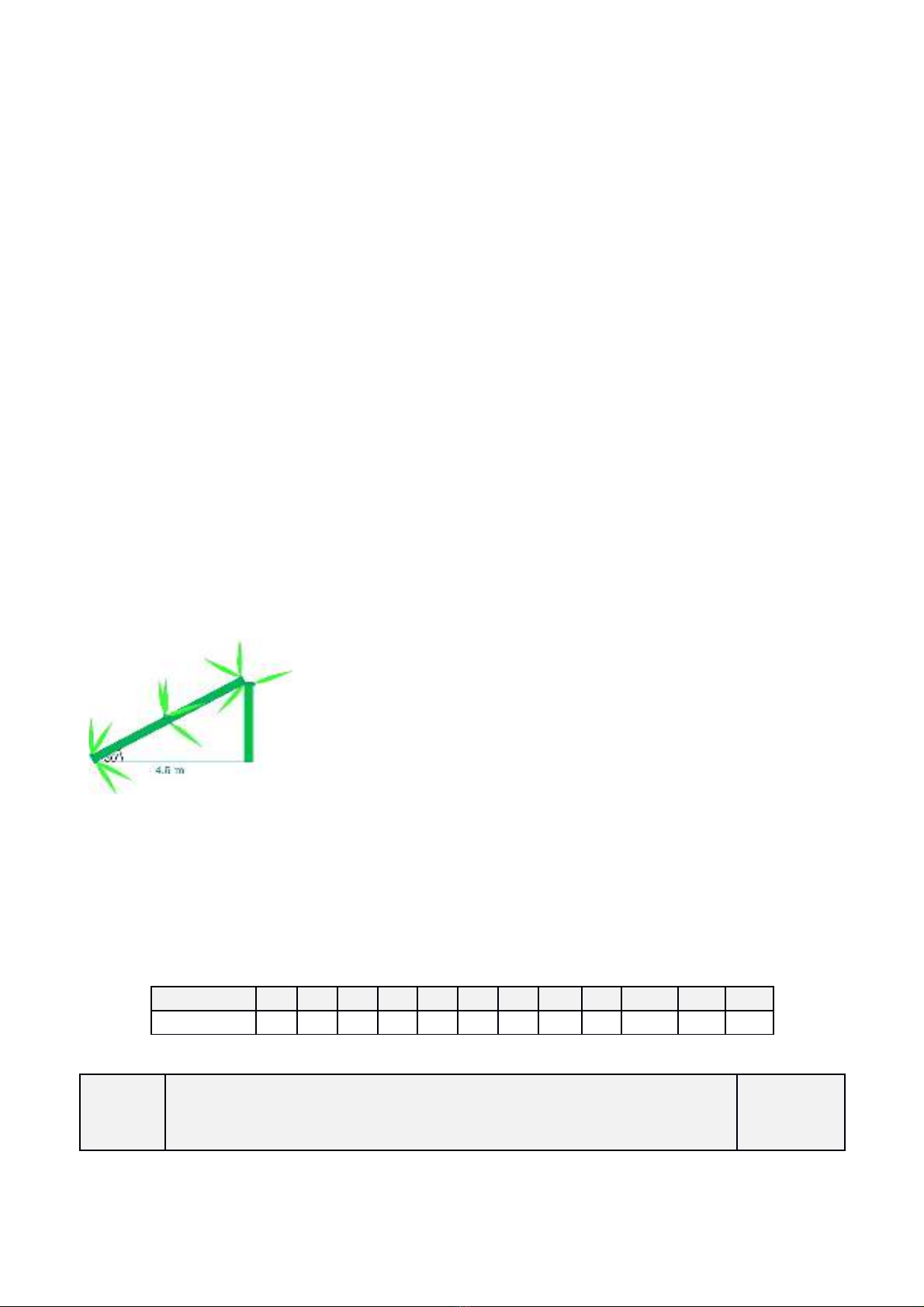
Một cây tre bị gãy ngang thân, ba điểm: gốc cây, điểm gãy và ngọn tre tạo thành một
tam giác vuông. Ngọn tre vừa chạm mặt đất và tạo với mặt đất một góc . Biết khoảng cách
từ vị trí ngọn tre chạm đất tới gốc cây bằng m. Hỏi trước khi cây tre bị gãy, cây tre cao
khoảng bao nhiêu mét? (kết quả làm tròn đến chữ số thập phân thứ hai)
---HẾT---
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. TRẮC NGHIỆM (3,0 điểm): Mỗi câu 0,25 điểm.
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Đáp án A C D C B C C D A B C B
II. TỰ LUẬN (7,0 điểm):
Bài Đáp án Biểu điểm
1
a) (x + 3) (x - 8) = 0 nên x + 3 = 0 hoặc x - 8 = 0
x + 3 = 0 Suy ra x = -3
x - 8 = 0 Suy ra x = 8
Vậy phương trình có hai nghiệm x = -3 và x = 8
b) = 1- < 1
= 1+ >1
Suy ra <
0,25
0,25
0,25
0,25
0,25
0,25
0,5
2
a)
Vậy nghiệm của hpt là (x,y) = (2;3)
b) Gọi chữ số hàng chục và hàng đơn vị lần lượt là x, y.
(ĐK: 0< y < x )
Tổng hai chữ số bằng 10, ta có phương trình x+y=10 (1)
Nếu viết hai chữ số đó theo thứ tự ngược lại thì được số mới nhỏ
hơn 18 đơn vị, ta có phương trình
(10x+y)- (10y+x)=18 hay 9x- 9y=18 hay x-y=2 (2)
Từ (1) và (2) ta có hệ phượng trình.
Giải hệ pt ta được: thoả mãn điều kiện
Vậy số cần tìm là 64.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
3
a) Theo tính chất tỉ số lượng giác của hai góc phụ nhau,
Ta có: cot650= tan 250: Sin550= cos350; cos530= Sin370;
tan820=cot80.
b) vuông tại A, có
Suy ra
vuông tại A, có AC=BC.sin B=10. sin 600 =5 cm;
AB = BC.cosB=10.cos 600 = 5cm
1,0
0,5
0,25
0,25
4Theo đề ta có hình vẽ
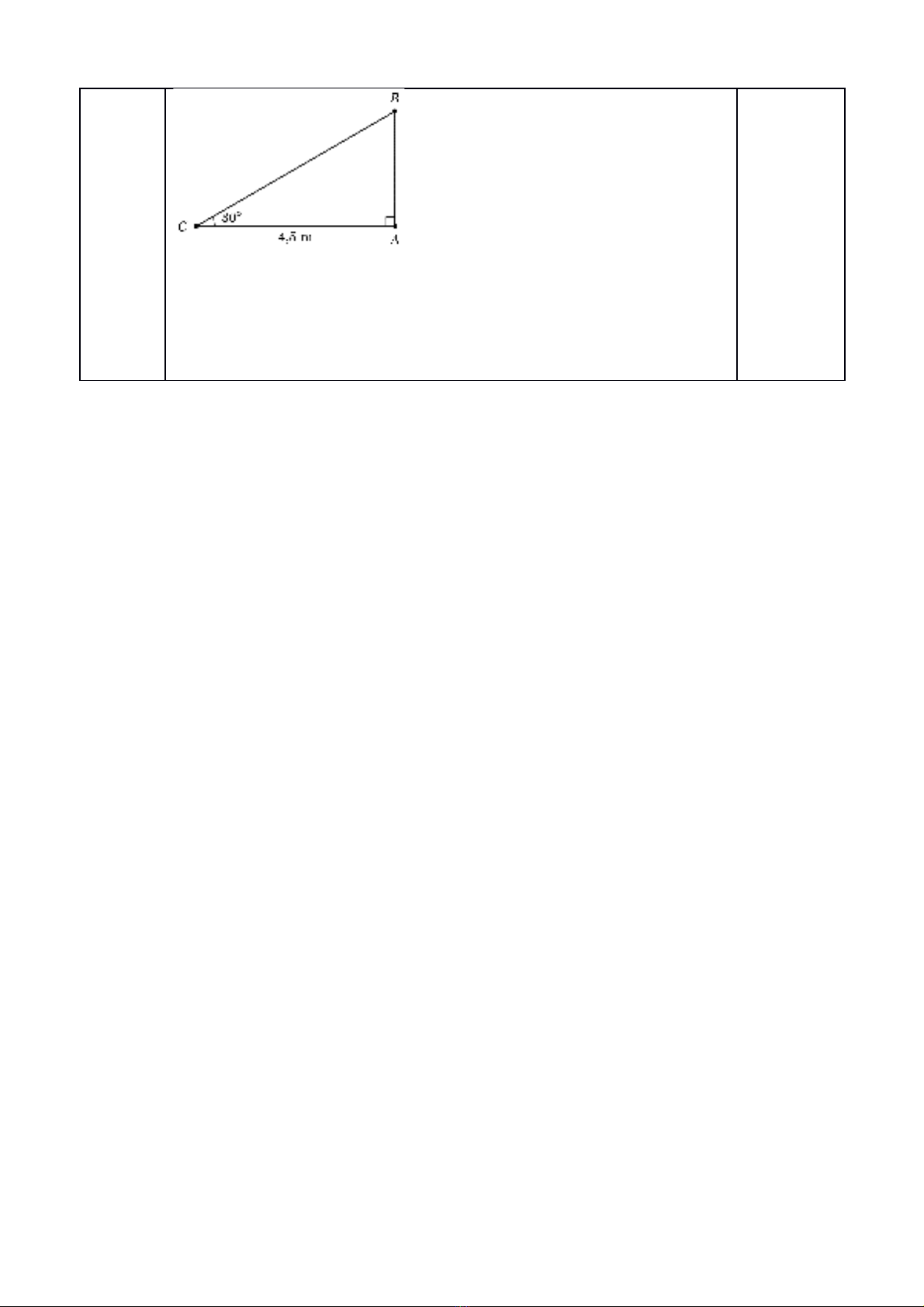
vuông tại A, ta có tanC= suy ra AB= AC.tanC=4,5.tan300= 2,60
vuông tại A, ta có cosC= suy ra BC= AC: cosC= 4,5:cos300= 5,20
Vậy chiều cao của cây tre là AB+BC= 2,60+ 5,20= 7,80 m.
0,25
0,25
0,25
0,25
(Lưu ý: Ở mỗi bài, học sinh có cách giải khác nhưng đúng và phù hợp với chương trình vẫn
cho điểm tối đa).
DUYỆT CỦA TỔ CHUYÊN MÔN GIÁO VIÊN RA ĐỀ
Nguyễn Đình Phương