TR NGTHCS KH NG ĐÌNHƯỜ ƯƠ
(Đ ki m tra g m 01 trang)ề ể ồ
KI M TRA GI A H C K II Ể Ữ Ọ Ỳ
NĂM H C: Ọ2020 – 2021
Môn: Toán 8
Th i gian làm bài: ờ90 phút
Bài 1(2,0 đi m) ểCho bi u th c : ể ứ
2
x -1
Ax 9 x -3
1
= +
−
và
x +3
2
B
=
v i x ≠ ± 3 ớ
a) Tính giá tr c a A khi ị ủ
1
23
x
= −
b) Rút g n bi u th c P =A:Bọ ể ứ
c) Tìm
x Z
đ P có giá tr là s nguyên.ể ị ố
Bài 2 (2,0 đi m) ểGi i ph ng trình sau:ả ươ
a)
2
( 1) ( 3 5) 0x x x x
− − − + =
b)
2
( 5) 6 30 0x x− + − =
c)
1 2
x 2 x x
2
2
x
x
− =
− −
Bài 3(2,0 đi m)ể. M t ôtô tr hàng đi t A đn B v i v n t c 50km/h. Sau khi đn B ôộ ở ừ ế ớ ậ ố ế
tô d ng l i đ giao hàng 30 phút r i quay v A v i v n t c 60 km/h. Tính quãngừ ạ ể ồ ề ớ ậ ố
đng AB, bi t r ng ườ ế ằ t ng ổth i gian ô tôờ đi, v và nghề ỉ là 6 gi .ờ
Bài 4(3,5 đi mể) Cho tam giác ABC vuông t i A. Qua A k đng cao AH (H ạ ẻ ườ
BC).
a) Ch ng minh r ng tam giác ABC đng d ng v i tam giác HAC.ứ ằ ồ ạ ớ
b) Khi cho AB=6cm; AC=8cm, tính đ dài đo n BC và AH?ộ ạ
c) T H kừ ẻ HE vuông góc v i AC t i E. Ch ng minh r ngớ ạ ứ ằ : HE2 = AE.AC.
d) G i I là trung đi m c a AH,EI c t AB t i F. Ch ng minh AHọ ể ủ ắ ạ ứ 2 = FA.FB + EA.EC
Bài 5(0,5 đi mể). Cho (a + b + c)2 = a2 + b2 + c2 và a, b, c khác 0.
Ch ng minh r ng: ứ ằ
.
………………….. H t……………………..ế
TR NG THCS KH NG ƯỜ ƯƠ
ĐÌNH
NĂM H C 2020-2021Ọ
H NG D N CH M Đ KI M TRAƯỚ Ẫ Ấ Ề Ể
GI A H C K II L P 8Ữ Ọ Ỳ Ớ
Môn ki m tra: ểTOÁN
Th i gian ki m tra: 90 phútờ ể
Bài Câu H ng d n ch mướ ẫ ấ Đi mể
1
(2đ)
a
o,5đ
T iạ x = -1 (tmđk) thay vào bi u th c A ta có:ể ứ
A= 0
0,25
0.25
b
0,5
2
2 2
2
2
1 1 2
:
9 3 3
1 3 3
9 9 2
1 3 3
9 2
2 2 3
9 2
1
3
x
P
x x x
x x x
x x
x x x
x
x x
x
x
x
−
� �
= +
� �
− − −
� �
− + −
� �
= +
� �
− −
� �
− + + −
=
−
+ −
=
−
+
=+
0,25
0,25
0.25
0.25
c
0,5
1 2
1
3 3
x
A Z
x x
+
= = −
+ +
=>
3x+
(2)Ư
=>
{ }
5; 4; 2; 1x− − − −�
0.25
0.25
2
(2đ)
A
(0.5)
x(x -1) -(x -3x +5)
2
2 2
0
3 5 0
2 4
2
x x x x
x
x
=
− − + − =�
=�
=�
V y nghi m c a pt là x = -1 và x = 5 ậ ệ ủ
0.25
0.25
B
0,75đ
b)
2
2
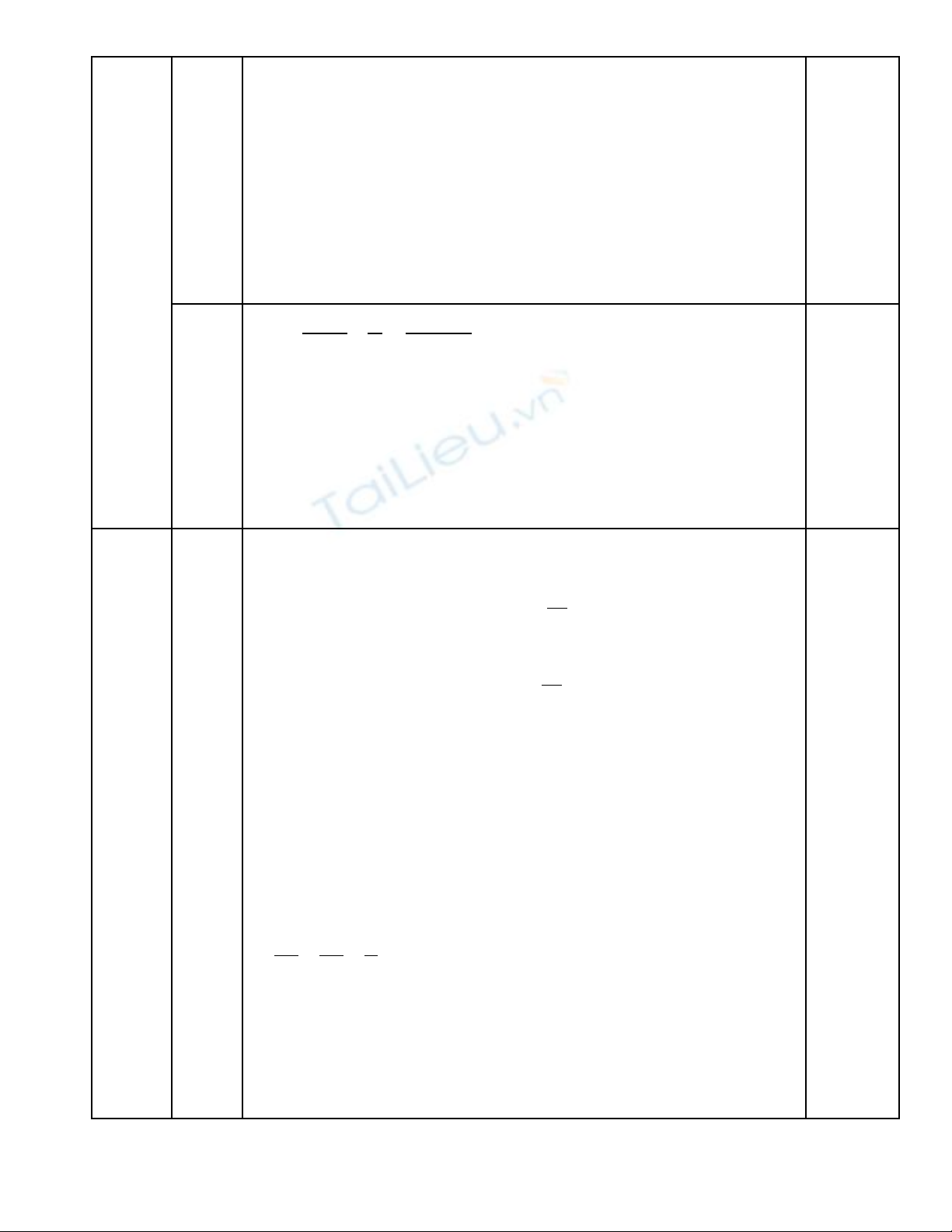
( 5) 6 30 0
( 5) 6( 5) 0
( 5)( 1) 0
5
1
x x
x x
x x
x
x
− + − =
− + − =�
− + =�
=
= −
V y nghi m c a pt là x = -1 và x = 5 ậ ệ ủ
0.25
0.25
0.25
C
0.75đ
c)
1 2
x 2 x x
2
2
2
x 0;x 2
2
- (x-2) = 2
x 0
x
x
x
x
− =
− −
− =�
x=0 và x=1( không th a mãn đi u ki n xác đnh)ỏ ề ệ ị
V y x=1 là nghi m c a ptậ ệ ủ
0.25
0,25
0.25
Bài 3
(2,0)
+ G i quãng đng AB là x (km) ( đi u ki n x>0).ọ ườ ề ệ
+Th i gian ô tô đi t A đn B là ờ ừ ế
( )
50
xh
.
+ Th i gian ô tô đi t B v A là ờ ừ ề
( )
60
xh
.
+ Do t lúc ô tô đi t A đn B lúc 7h, ngh B 30 phút r i ừ ừ ế ỉ ở ồ
quay v A lúc 13h , nên th i gian ô tô th c hi n là 13-ề ờ ự ệ
7=6(h).
V y ta có pt: ậ
V y quãng đng AB dài 150kmậ ườ
0,25
0,25
0,25
0,25
0,25
0,5
0,25
Bài 4
(3,5)
0,5đ
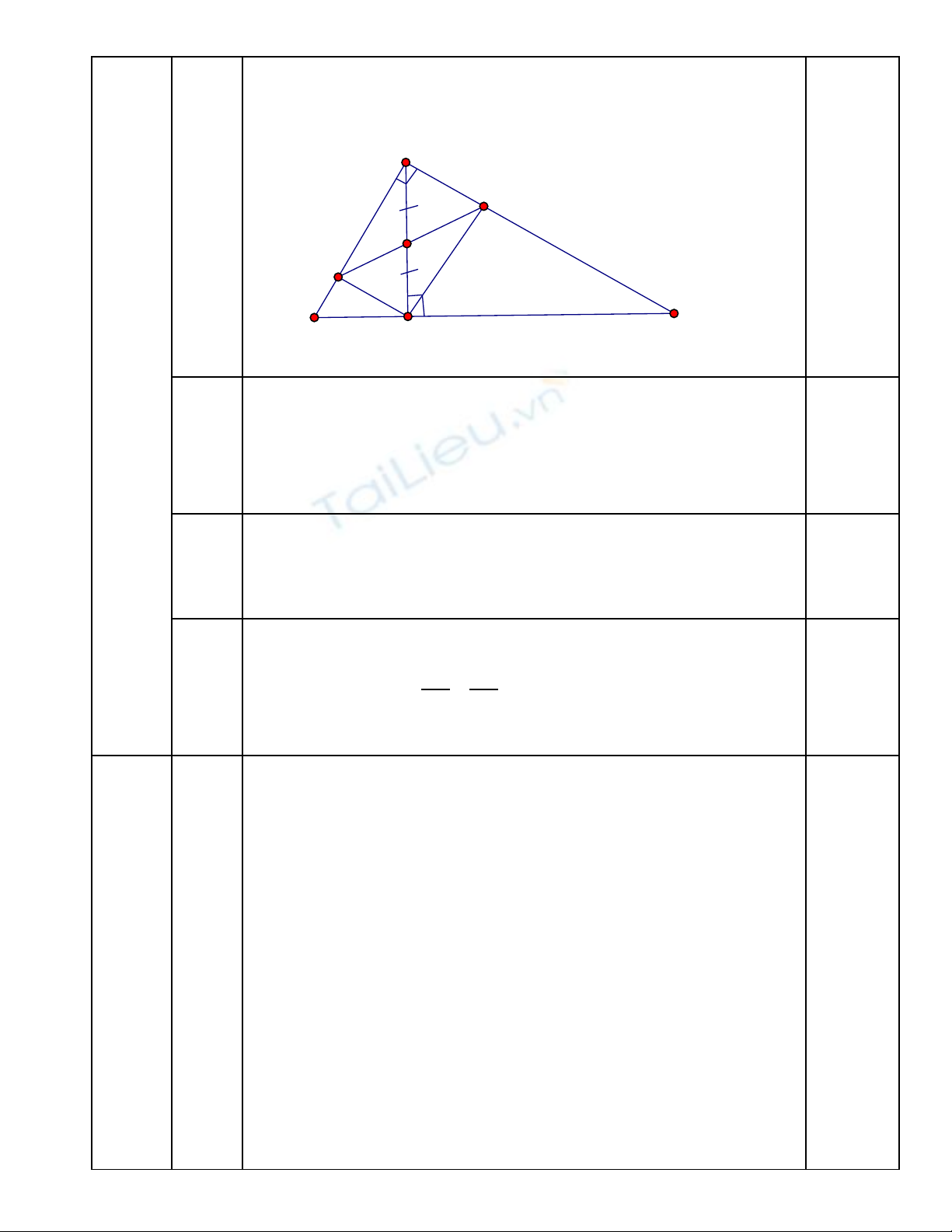
Ghi gi thi t, k t lu n và v hình đúng đn câu aả ế ế ậ ẽ ế
I
A
B
C
H
E
F
0,5đ
Câu a
1đ
a) Ch ng minh : ∆ABCứ ∽∆HAC
Ch ra đc hai c p góc b ng nhauỉ ượ ặ ằ
K t lu n : ∆ABCế ậ ∽∆HAC (g.g)
0,25
0,25
0,5
Câu b
0,75đ
+)Tính đc BC=10cm ượ
+)AH = 4,8cm
0,25
0,5
Câu c
0,75đ
Ch ng minh đc: ∆EAHứ ượ ∽∆EHC
Vi t đc t s : : ế ượ ỉ ố
2
.EC
EH EA EH EA
EC EH
= =�
0,25
0,25đ
0,25
Câu d
0,5đ
+) Ch ng minh tg AFHE là hình ch nh t:ứ ữ ậ
- Ch ng minh AF// HE ứ
- Ch ng minh tam giác AIF b ng tam giác HIEứ ằ
=>AF=HE mà AF// HE nên tg AFHE là hình bình hành,l i có ạ
góc AEH vuông nên tg AFHE là hình ch nh t => HF vuông ữ ậ
góc v i AB và AH=EF (1)ớ
+) CM đc ∆FAHượ ∽∆FHB (g.g) => HF2 = FA.FB (2)
0,25
0,25
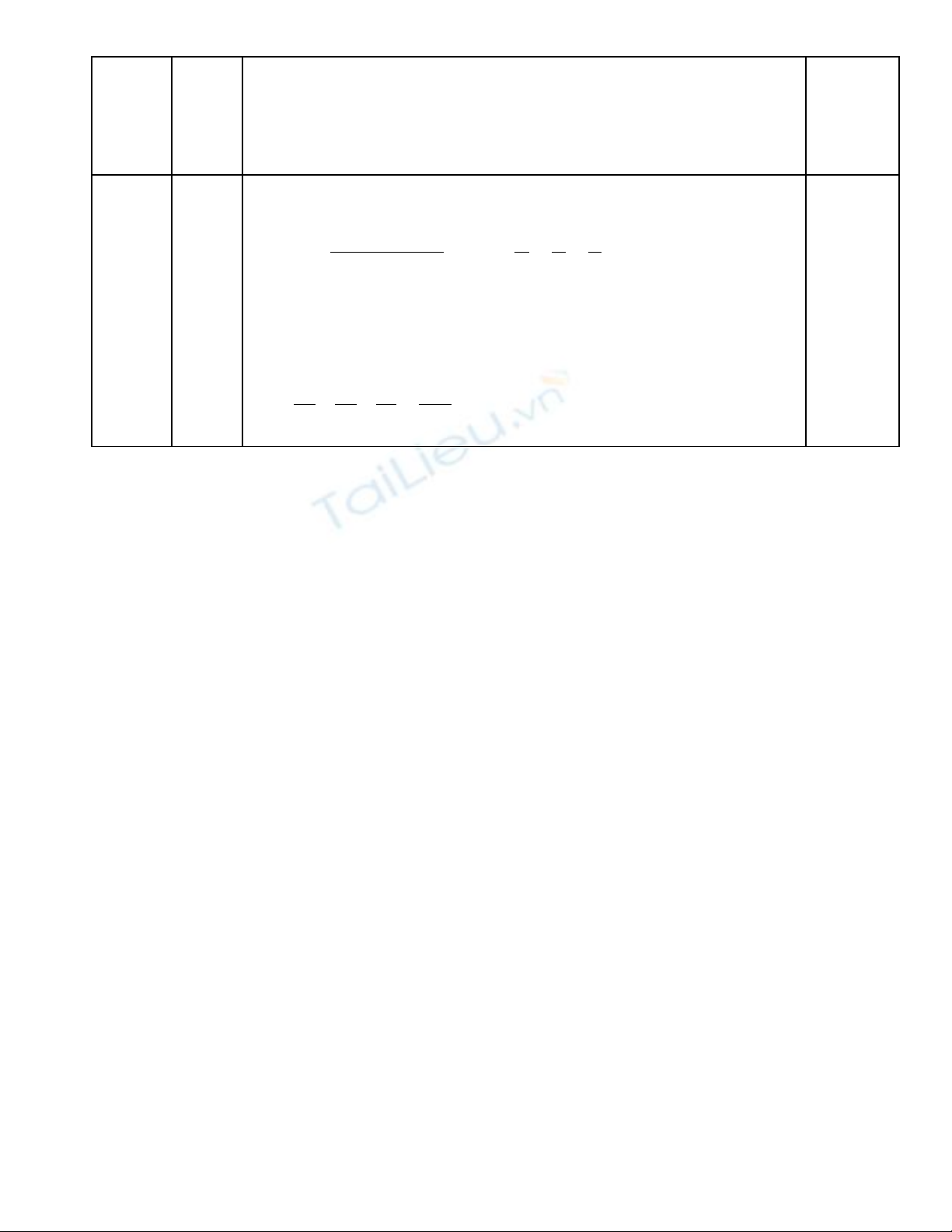
Theo (b) có HE2 = EA.EC (3) .
+) Xét tam giác HEF vuông t i H. Có EFạ2 = HF2 + HE2 (4)
Thay (1),(2),(3) vào (4) ta có: AH2 = FA.FB + EA.EC
Bài 5
(0,5)
0,5đ
T gi thi t ta có ab+bc+ca=0ừ ả ế
Do đó :
1 1 1
0 0
ab bc ca
abc a b c
+ + = + + =�
Sau đó ta ch ng minh n u x + y + z = 0 thì xứ ế 3 + y3 + z3 =
3xyz.
V yậ
3 3 3
1 1 1 3
a b c abc
++=
0,25
0,25
Ng i ra đ Nhóm tr ng chuyên môn T tr ng chuyên ườ ề ưở ổ ưở
môn
Tr n Th H i Y n Nguy n Th H ng Nguy n Th ầ ị ả ế ễ ị ườ ễ ế
Th ngắ