SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC NINH
(Đề có 01 trang)
ĐỀ KIỂM TRA GIỮA HỌC KỲ 2
NĂM HỌC 2023 – 2024
Môn: Toán – Lớp 8
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Phân thức đối của phân thức 3
2
5
y
x
là
A. 3
2
5
y
x
. B. 3
2
5
y
x
. C.
3
5
2
x
y
. D.
3
5
2
x
y
.
Câu 2. Điều kiện xác định của phân thức
5
2024
x
x
là
A.
5x
. B.
5x
. C.
2024x
. D.
2024x
.
Câu 3. Mẫu thức chung của hai phân thức 3 4
3
2x y
, 4 3
4
5x y
là
A. 4 4
10x y
. B. 4 3
10x y
. C. 3 4
10x y
. D. 4 4
x y
.
Câu 4. Cho
ABC
và
MNP
có
,A P B N
. Khẳng định nào sau đây đúng?
A.
ABC MNP
. B.
ABC NMP
. C.
ABC PMN
. D.
ABC PNM
.
Câu 5. Cho
ABC
vuông tại
A
. Khẳng định nào dưới đây đúng?
A. 2 2 2
AB BC AC
. B. 2 2 2
BC AC AB
.
C.2 2 2
AC BC AB
. D. 2 2 2
2AB AC BC
.
Câu 6. Cho các cặp hình sau, tìm cặp hình không đồng dạng?
A. Hình 3. B. Hình 1. C. Hình 4. D. Hình 2.
II. TỰ LUẬN (7,0 điểm)
Câu 7. (1,5 điểm) Thực hiện phép tính:
a)
3 6
2 2
x
x x
. b)
2
2
3 1
16
x x
xx
. c) 2 2
4 10
:
4 2x x x
.
Câu 8. (2,0 điểm) Cho biểu thức
2
2
5 2 3 2 9
3 3 9
x x
Ax x x
(với
3, 3x x
).
a) Rút gọn biểu thức
A
.
b) Tính giá trị biểu thức
A
khi
1x
.
c) Tìm các giá trị nguyên của
x
để biểu thức
A
có giá trị nguyên.
Câu 9. (3,0 điểm) Cho
ABC
vuông tại
A
(
AB AC
) có đường cao
AD
.
a) Chứng minh
DAB ACB
.
b) Tia phân giác của góc
ABC
cắt
AC
tại
E
. Từ
C
kẻ đường thẳng vuông góc với đường thẳng
BE
tại
F
.
Chứng minh rằng
. .AE AB EC BD
.
c) Chứng minh rằng 2
. .EC AC EB BF BC
.
Câu 10. (0,5 điểm) Một tàu thủy du lịch xuất phát từ Hà Nội đi đến Việt Trì, sau đó nghỉ lại tại Việt Trì
2
giờ
trước khi quay trở lại Hà Nội. Quãng đường từ Hà Nội tới Việt Trì là
74
km. Vận tốc của dòng nước là
5
km/h. Gọi vận tốc thực của tàu thủy là
x
(km/h). Viết biểu thức biểu thị thời gian kể từ lúc tàu xuất phát đến
khi quay trở về Hà Nội.
-------- Hết--------
Hình 1
Hình 2
Hình 3
Hình 4
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Mỗi câu đúng được 0,5 điểm.
Câu 1 2 3 4 5 6
Đáp án
B
C
A
D
B
C
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu
ớng dẫn
Đi
ểm
Câu 7
1,5
a)
3 6 3 6 3( 2)
3
2 2 2 2
x x x
x x x x
0,5
b)
2
2
2 2 2
3 1
3 1 3 ( 1)( 1) 1
1 2
6 ( 1)6 6 ( 1)
x x
x x x x x x
x x
x x x x x
0,5
c) 2 2
4 10 4 ( 2) 2
:
( 2)( 2) 10 5( 2)
4 2
x x x
x x x
x x x
0,5
Câu 8
2,0
a)
2
2
5 2 3 2 9
3 3
9
x x
A
x x
x
2
5( 3) 2( 3) 3 2 9
( 3)( 3) ( 3)( 3) ( 3)( 3)
x x x x
x x x x x x
0,5
2 2
5 15 2 6 3 2 9 3 9 3 ( 3) 3
( 3)( 3) ( 3)( 3) ( 3)( 3) 3
x x x x x x x x x
x x x x x x x
0,5
b) Thay
1
x
(thỏa mãn) vào biểu thức
A
ta được
3.1 3
1 3 4
A
0,5
c) Ta có
3 9
3
3 3
x
A
x x
0,25
Biểu thức
A
có giá trị nguyên khi
9
3
x
có giá trị nguyên. Khi
3 { 9; 3; 1;1; 3;9}
x
giải ra được
{ 12; 6; 4; 2;0;6}
x
(thỏa mãn)
0,25
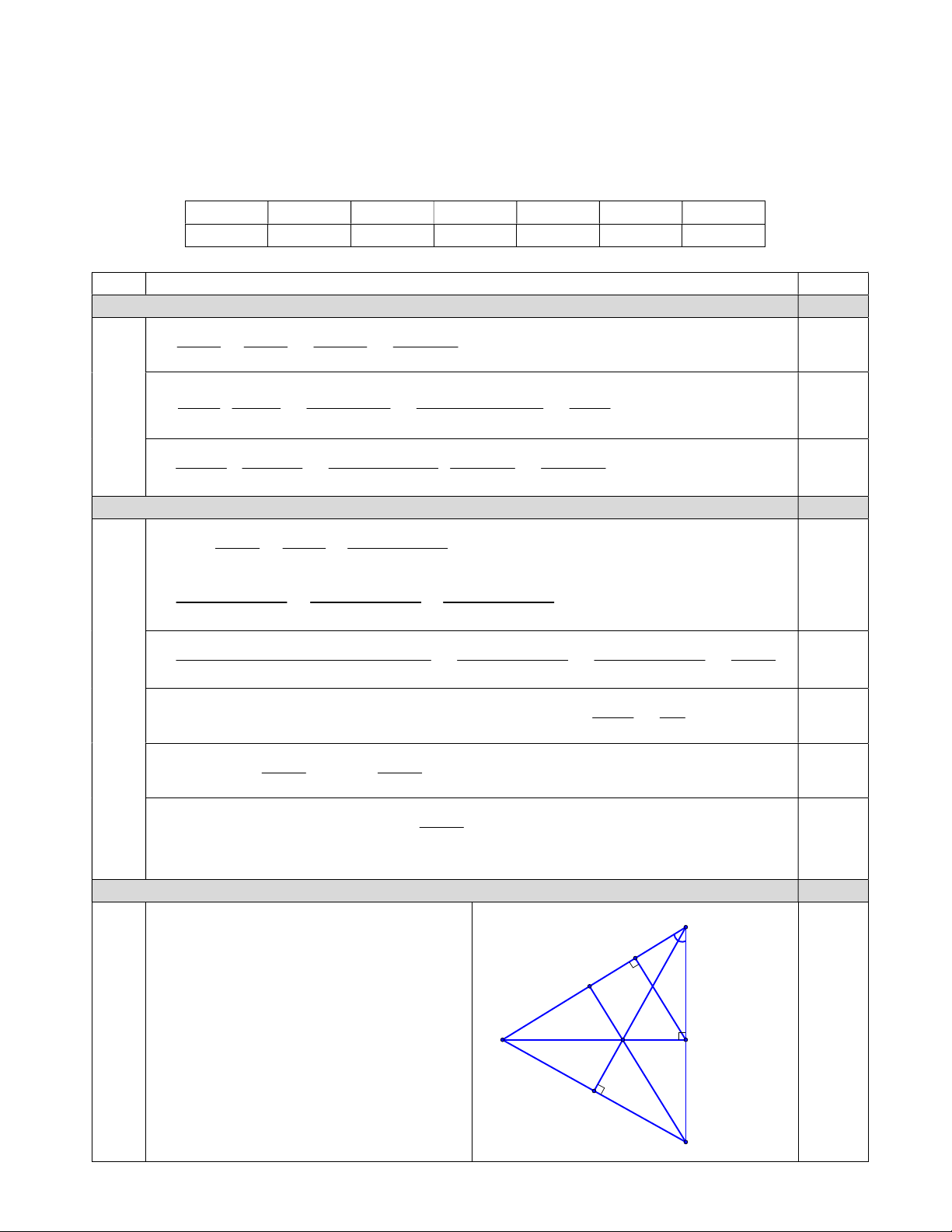
Câu 9.a
1,5
Vẽ hình ghi GT, KL đúng
0,5
N
M
F
E
D
C
B
A
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC NINH
¯¯¯¯¯¯¯¯¯¯
HƯỚNG DẪN CHẤM
KIỂM TRA GIỮA HỌC KỲ 2
NĂM HỌC 2023 – 2024
Môn: Toán – Lớp 8
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Xét
DAB
và
ACB
có
CBA
chung
0,5
90 ( )
ADB CAB DAB ACB g g
0,5
Câu 9.b
1,0
Từ
AB BD
DAB ACB
BC AB
(1) 0,25
Do
BE
là đường phân giác của
AB AE
ABC
BC EC
(2) (tính chất đường phân
giác c
ủ
a tam giác)
0,5
Từ (1) và
(2) . .
BD AE
AE AB EC BD
AB EC
0,25
Câu 9
.
c
0
,5
Gọi
M
là giao điểm của
AB
và
CF
.
Gọi
N
là giao điểm của
ME
và
BC
.
Chỉ ra
E
là trực tâm của
BCM
suy ra
ME
vuông góc với
BC
tại
N
.
Chứng minh
( ) . .
ECN BCA g g EC AC CN BC
( ) . .
ENB CFB g g EB BF NB BC
(4)
0,25
Cộng vế với vế của (3) và (4) ta được
. . . .
EC AC EB BF CN BC NB BC
. . ( ).
EC AC EB BF CN NB BC
2
. .
EC AC EB BF BC
(
đpcm)
0,25
Câu 10.
0
,5
Vận tốc xuôi dòng là
5
x
(km/h)
Vận tốc ngược dòng là
5
x
(km/h) 0,25
Biểu thức biểu thị thời gian kể từ lúc tàu xuất phát đến khi quay trở về Hà Nội là
74 74
2
5 5
x x
(giờ). 0,25
Lưu ý: Học sinh làm cách khác đúng cho điểm tối đa