UBND QUẬN BÌNH THẠNH
TRƯỜNG TRUNG HỌC CƠ SỞ
NGUYỄN VĂN BÉ
ĐỀ THAM KHẢO
(Đề kiểm tra có 02 trang)
KIỂM TRA GIỮA KỲ HỌC KỲ 2
NĂM HỌC: 2023 - 2024
MÔN: TOÁN - LỚP 8
Thời gian làm bài: 90 phút, không kể thời gian phát đề
I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm). Hãy chọn đáp án đúng nhất
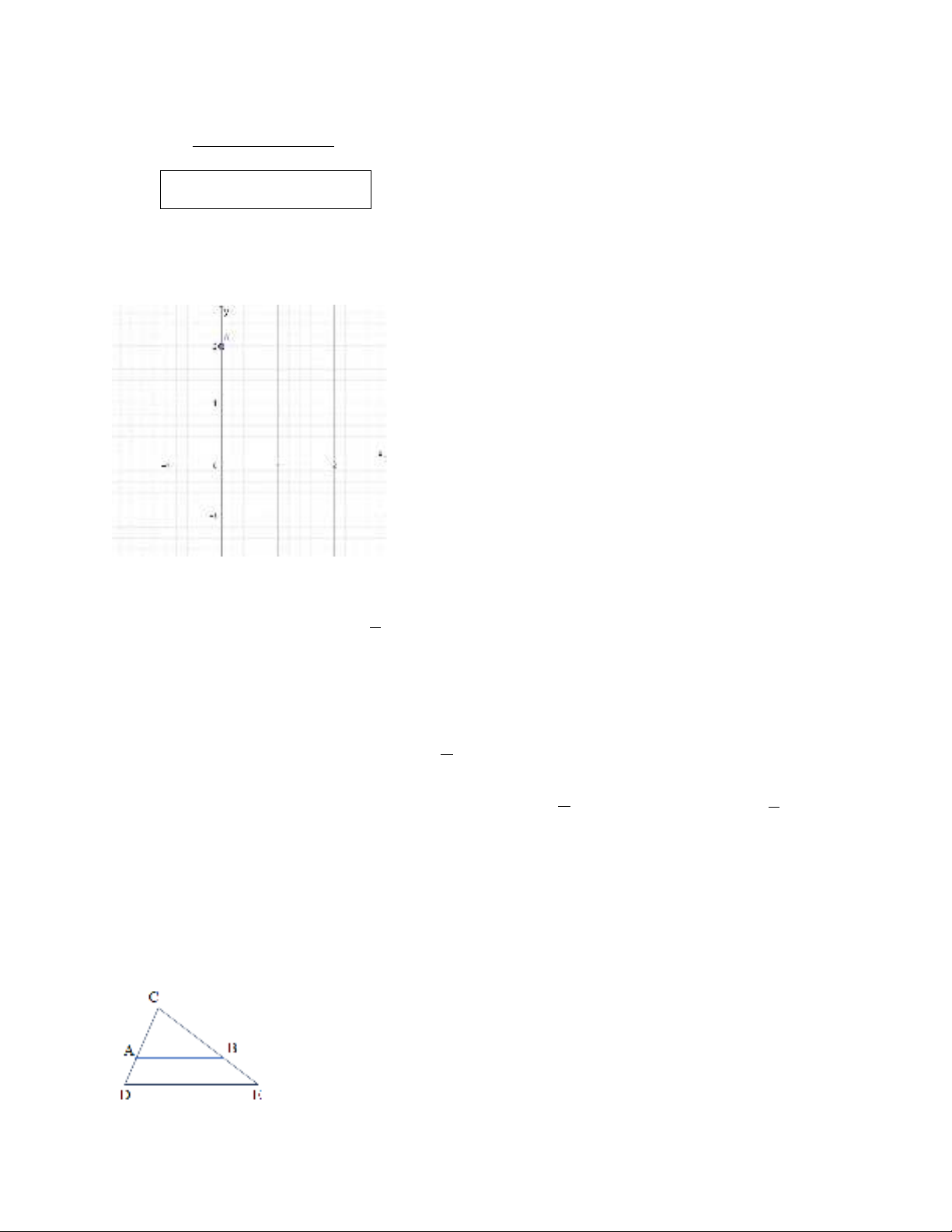
Câu 1. Cho mặt phẳng tọa độ
Oxy
và điểm
A
(như hình vẽ).
Khi đó tọa độ của điểm
A
là:
A. A(0;0) B. A(2;2) C. A(2;0) D. A(0;2)
Câu 2. Đồ thị của hàm số y =
1
3
x là đường thẳng OM với O ( 0 ; 0 ) và
A. M( 1 ; 3 ) B. M( -1 ; -3 ) C. M( 3 ; 1 ) D. M(-3 ; 1 )
Câu 3. Hệ số a, b trong hàm số bậc nhất
45yx
lần lượt là
A.
4 ; -5x
B.
C.
4; 5
D.
4; 5
Câu 4. Hệ số góc của đường thẳng
1
2

x
y
là
A. 1 B. 2 C.
2
x
D.
1
2
Câu 5. Đồ thị của hàm số
21yx
và hàm số
3y ax
là hai đường thẳng song song.
Hãy tìm hệ số a
A.
3a
B.
2a
C.
0a
D.
1a
Câu 6. Điểm nào sau đây thuộc đồ thị hàm số
24yx
A.
0; 4M
B.
0; 4N
C.
4; 0N
D.
4; 0N
Câu 7. Cho hình vẽ:
Biết
//AB DE
, áp dụng định lí Thales ta có hệ thức đúng là
A.
CD AB
CE DE
B.
AC BC
CD CE
C.
CA AB
CD DE
D.
AC CE
BC CD
Câu 8. Cho hình vẽ:
Khẳng định nào sau đây là sai?
A. MN là đường trung bình của ∆ABC B. MP là đường trung bình của ∆ABC
C. PQ là đường trung bình của ∆BCI D. MN là đường trung bình của ∆ABI
Câu 9. Cho tam giác ABC biết AM là đường phân giác (M ∈ BC). Trong các khẳng định sau,
khẳng định nào đúng?
A.
AM AB
MC AC
=
B.
BM AB
MC AC
=
C.
BM AM
MC AC
=
D.
AB AM
AC BC
=
Câu 10. Cho
ABC
có
4; 9AB cm AC cm
. Gọi AD là tia phân giác của
BAC
. Tính tỉ
số
CD
BD
A.
9
4
B.
4
9
C.
4
5
D.
5
4
Câu 11. Nếu
~ABC A B C


theo tỉ số
2k
thì
~A B C ABC


theo tỉ số là
A. 2 B.
1
2
C.
1
4
D. 4
Câu 12. Nếu tam giác ABC có MN // BC (với M Є AB, N Є AC) thì
A. ΔAMN đồng dạng với ΔACB B. ΔABC đồng dạng với MNA
C. ΔMAN đồng dạng với ΔBAC D. ΔABC đồng dạng với ΔANM
II. TỰ LUẬN: (7,0 điểm)
Bài 1 (1,5 điểm)
a) Cho hàm số
2
31y fx x 
. Tính các giá trị sau:
1; ( 1)
2


ff
b) Cho hàm số y = (m − 1)x + m. Tìm m để hàm số đã cho là hàm số bậc nhất.
c) Tìm m để hai hàm số bậc nhất
y 2mx 3
(với m ≠ 0) và
y 6x 1
có đồ thị là hai
đường thẳng song song với nhau.
Bài 2 (2,0 điểm)
a) Vẽ các đồ thị hàm số sau trên cùng một mặt phẳng tọa độ
( )
1
: 35dyx= +
và
2
1
:3
dy x
b) Xác định đường thẳng (d) :
y ax b a 0
đi qua A(1;5) và cắt trục tung tại điểm có tung
độ bằng 1.
Bài 3 (0,75 điểm) Nhà máy A sản xuất lô áo với giá vốn là
45000000 đồng và giá bán lẻ mỗi chiếc áo là 300000 đồng. Khi đó
gọi y (đồng) là số tiền lời (hoặc lỗ) của nhà máy thu được khi bán x
cái áo .
a/ Viết hàm số y biểu diễn số tiền lời (hoặc lỗ) của nhà máy thu
được khi bán x cái áo.
b/ Hỏi nhà máy A phải bán bao nhiêu cái áo để có số tiền lời 15000000
đồng?
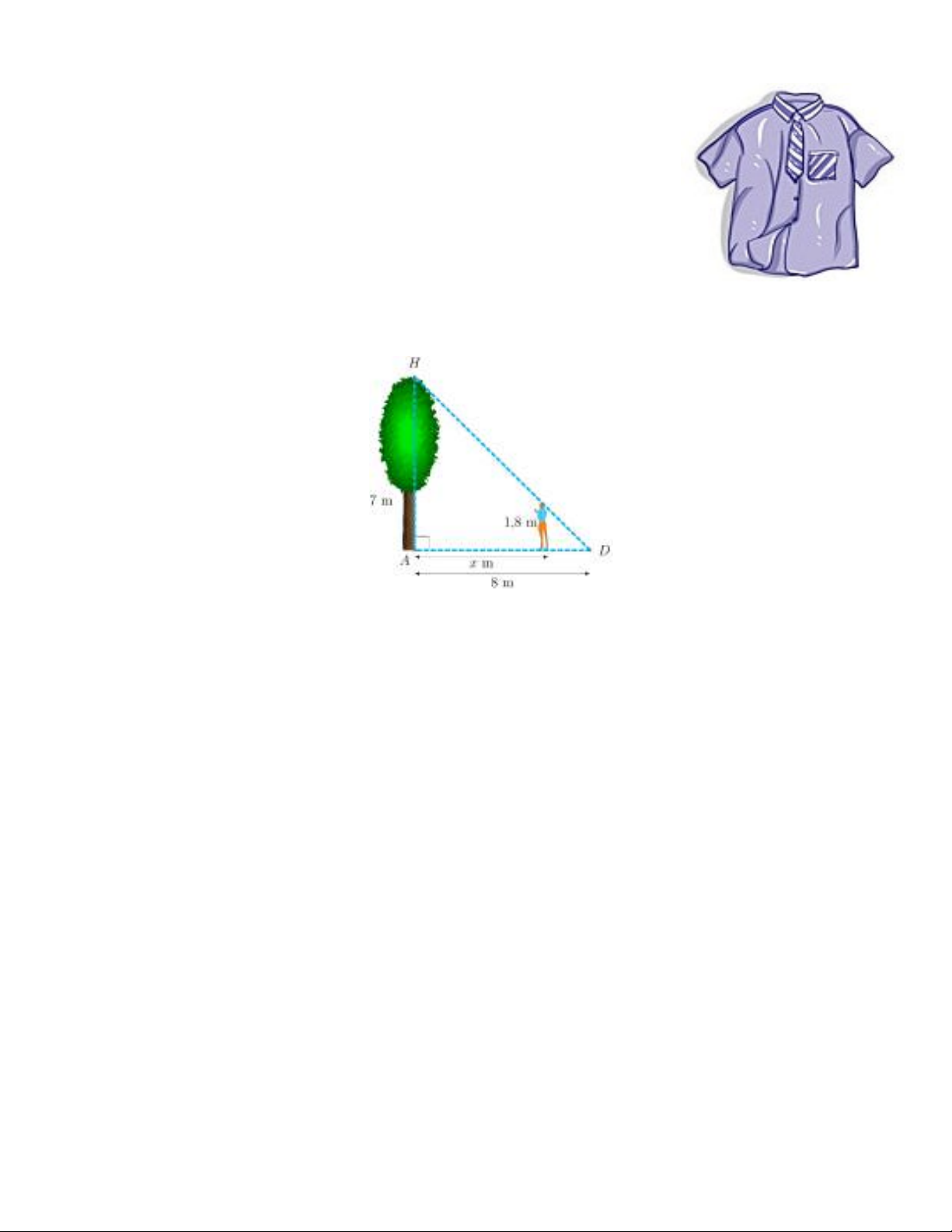
Bài 4 (0,75 điểm) Một cây xanh cao 7m, đổ bóng nắng dài 8m trên
đường như hình bên dưới. Một người cao 1,8m muốn đứng trong bóng râm của cây. Hỏi
người đó có thể đứng cách gốc cây xa nhất bao nhiêu mét? (kết quả làm tròn đến chữ số thập
phân thứ nhất)
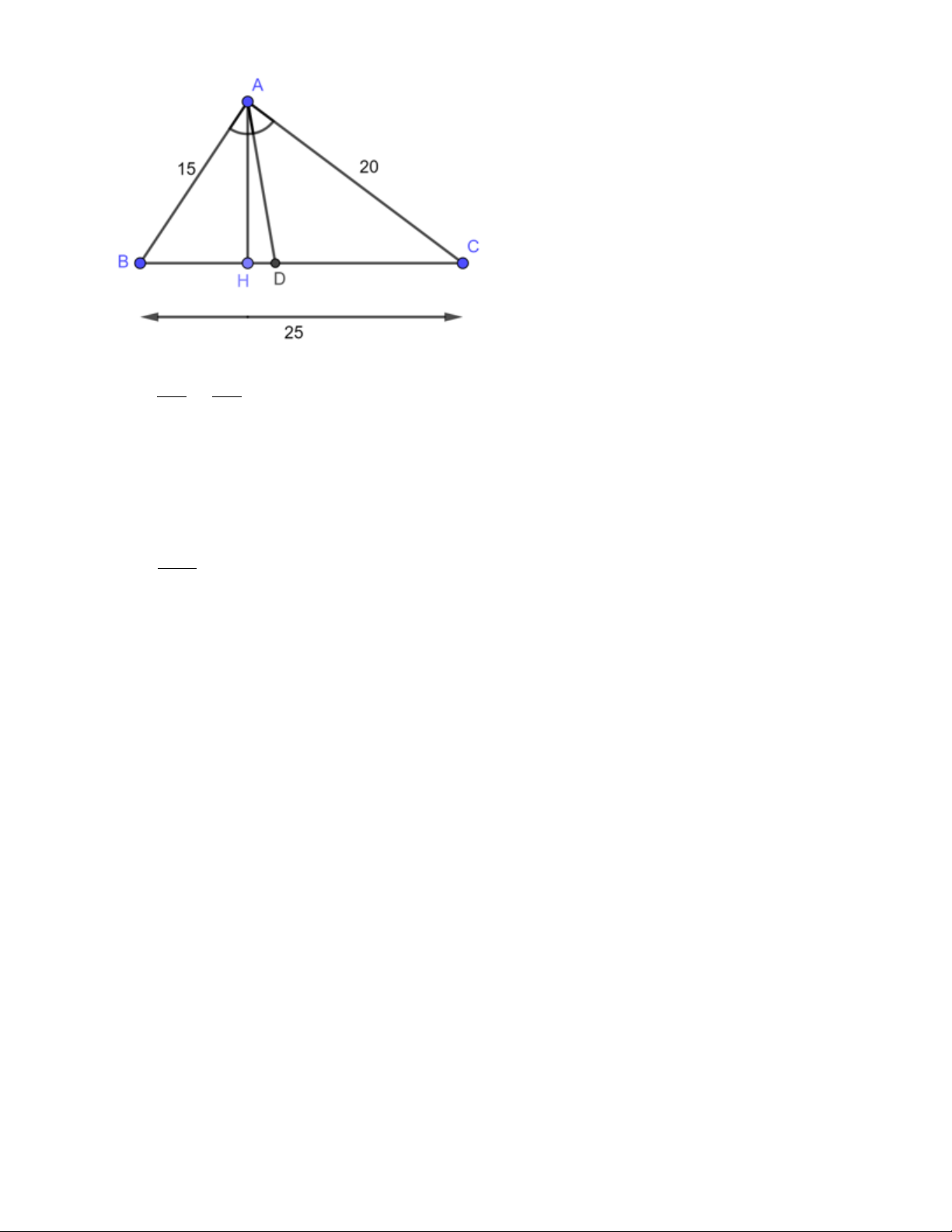
Bài 5 (2,0 điểm) Cho tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân
giác của góc BAC cắt BC tại D.
a) Tính độ dài các đoạn thẳng DB, DC
b) Tính diện tích các tam giác ABD, ACD
---HẾT---
ĐÁP ÁN
I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Trả lời
D
C
C
D
B
A
B
A
B
A
B
C
II. TỰ LUẬN: (7,0 điểm)
Bài 1 (1,5 điểm)
a)
2
31y fx x 
2
11 7
3. 1
22 4
f 









 
0,25 đ
2
1 3. 1 1 4f 
0,25 đ
b) y = (m − 1)x + m là hàm số bậc nhất
⇒ m – 1 ≠ 0 ⇒ m ≠ 1 0,5 đ
c) Để hai hàm số
y 2mx 3
(với m ≠ 0) và
y 6x 1
có đồ thị là hai đường thẳng
song song với nhau thì 2m = 6 ⇒ m = 3 0,5 đ
Bài 2 (2,0 điểm)
a) Bảng giá trị 0,5 đ
Vẽ
( )
1
: 35dyx= +
và
2
1
:3
dy x
0,5 đ
b) đường thẳng (d) :
y ax b a 0
đi qua A(1;5) ⇒ 5 = a + b 0,5 đ
đường thẳng (d) :
y ax b a 0
cắt trục tung tại điểm có tung độ bằng 1
⇒ b = 1 0,25 đ
a = 2, b = 1
y = 2x + 1 0,25 đ
Bài 3 (0,75 điểm)
a) Công thức biểu diễn y theo x là : y = 50 000 000 – 400 000.x
b) Ta có :
45 000 000 – 300 000. x = 15 000 000
300 000. x = 45 000 000 – 15 000 000
300 000 . x = 30 000 000
x = 30 000 000 : 300 000 = 100
Vậy nhà máy A phải bán được 100 cái áo để có số tiền lời 15000000 đồng
Bài 4 (0,75 điểm)
Công thức 0,25 đ
Thay số 0,25 đ
Kết quả 0,25 đ
Kết luận 0,25 đ
Bài 5 (2,0 điểm)
a) Tính DB, DC
CM:
DB AB
DC AC
0,25 đ
Tính DB 0,5 đ
Tính DC 0,25 đ
b) Tính diện tích các tam giác ABD, ACD
CM: ∆ABC vuông 0,25 đ
Tính SABC 0,25 đ
Tính
ABD
ACD
S
S
0,25 đ
Tính
ABD ACD
S ,S
0,25 đ