SỞ GD ĐT NAM ĐỊNH ĐỀ KIỂM TRA GIỮA KÌ II
TRƯỜNG THCS ĐÀO SƯ TÍCH NĂM HỌC 2022 -2023
MÔN TOÁN LỚP 9
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
PHÂ'N TRĂ(C NGHIÊ*M (2 điêm)
Hay chon phương an tra lơi đung băng cach viêt chư cai đưng trươc phương an đo vao bai
lam cua minh:
Câu 1: Gia# tri% cua biêu thư#c
2 8
+
bă*ng:
A.
10
B.
3 2
C.
6
D.
2 4
+
Câu 2: Biêu thư#c
1 2x x
− + −
co# y# nghi4a khi:
A.
2x
<
B.
2x
C.
1x
D.
Câu 3: Đươ*ng thăng
(2 1) 3y m x
= − +
song song vơ#i đươ*ng thăng
3 2y x= −
khi:
A.
2m
=
B.
2m
= −
C.
2m
D.
2m
−
Câu 4: Hê% phương tri*nh
2 3
3
x y
x y
− =
+ =
co# nghiê%m
( ; )x y
bă*ng:
A.
( 2;5)
−
B.
(0; 3)
−
C.
(1;2)
D.
(2;1)
Câu 5: Đô* thi% ha*m sô#
2
y x= −
đi qua điêm:
A.
(1;1)
B.
( 2;4)−
C.
(2; 4)−
D.
( 2; 1)
−
Câu 6: Tam gia#c ABC vuông ta%i A co# AB=4cm, AC=3cm thi* đô% da*i đươ*ng cao AH cua tam
gia#c ABC bă*ng:
A.
3
4
cm B.
12
5
cm C.
5
12
cm D.
4
3
cm
Câu 7: Tam gia#c ABC vuông ta%i A, biê#t AC=3cm, BC=5cm, khi đo# tanB co# gia# tri% bă*ng:
A.
3
4
B.
3
5
C.
4
3
D.
5
3
Câu 8: Đươ*ng tro*n la* hi*nh:
A.Không co# tru%c đô#i xư#ng C.Co# 2 tru%c đô#i xư#ng
B.Co# 1 tru%c đô#i xư#ng D.Co# vô sô# tru%c đô#i xư#ng
PHÂ'N TƯ* LUÂ*N (8 điêm)
Ba*i 1 : (1,5 điêm)
1)Ti#nh:
1
3 2 2 2 1
+ + +
2)Ru#t go%n
3 3
.9
3 3
x x
Ax
x x
+
= +
+
+ −
vơ#i
0x
va*
9x
Ba*i 2: (1,5 điêm)
Cho ha*m sô#
2
3y kx k= − + +
(d)
1)Ti*m
k
đê đô* thi% ha*m sô# că#t tru%c hoa*nh ta%i điêm co# hoa*nh đô% la* 4
2)Ti*m
k
biê#t đô* thi% ha*m sô# (d) la* đươ*ng thăng song song vơ#i đươ*ng thăng
5 6y x= +
Ba*i 3: (1,0 điêm)
Cho hê% phương tri*nh:
1
2 4
mx y
x my
− = −
+ =
Ti*m tâ#t ca ca#c gia# tri% cua
m
đê hê% phương tri*nh co# nghiê%m duy nhâ#t
( ; )x y
thoa ma4n
2x y+ =
Ba*i 4: (3,0 điêm)
Cho đươ*ng tro*n
( ; )O R
va* 1 điêm A nă*m ngoa*i đươ*ng tro*n. Tư* A ve4 2 tiê#p tuyê#n AB va*
AC (B,C la* tiê#p điêm). Ve4 đươ*ng ki#nh BD, đươ*ng thăng vuông go#c vơ#i BD ta%i O că#t đươ*ng
thăng DC ta%i E.
a) Chư#ng minh: DC//OA
b) Chư#ng minh: Tư# gia#c AEDO la* hi*nh bi*nh ha*nh
c) Đươ*ng thăng BC că#t OA va* OE lâ*n lươ%t ta%i I va* K
Ba*i 5: (1,0 điêm)
Giai phương tri*nh:
2
2 2 ( 2) 3 2 0x x x x− − − + + =
------------HÊ#T------------
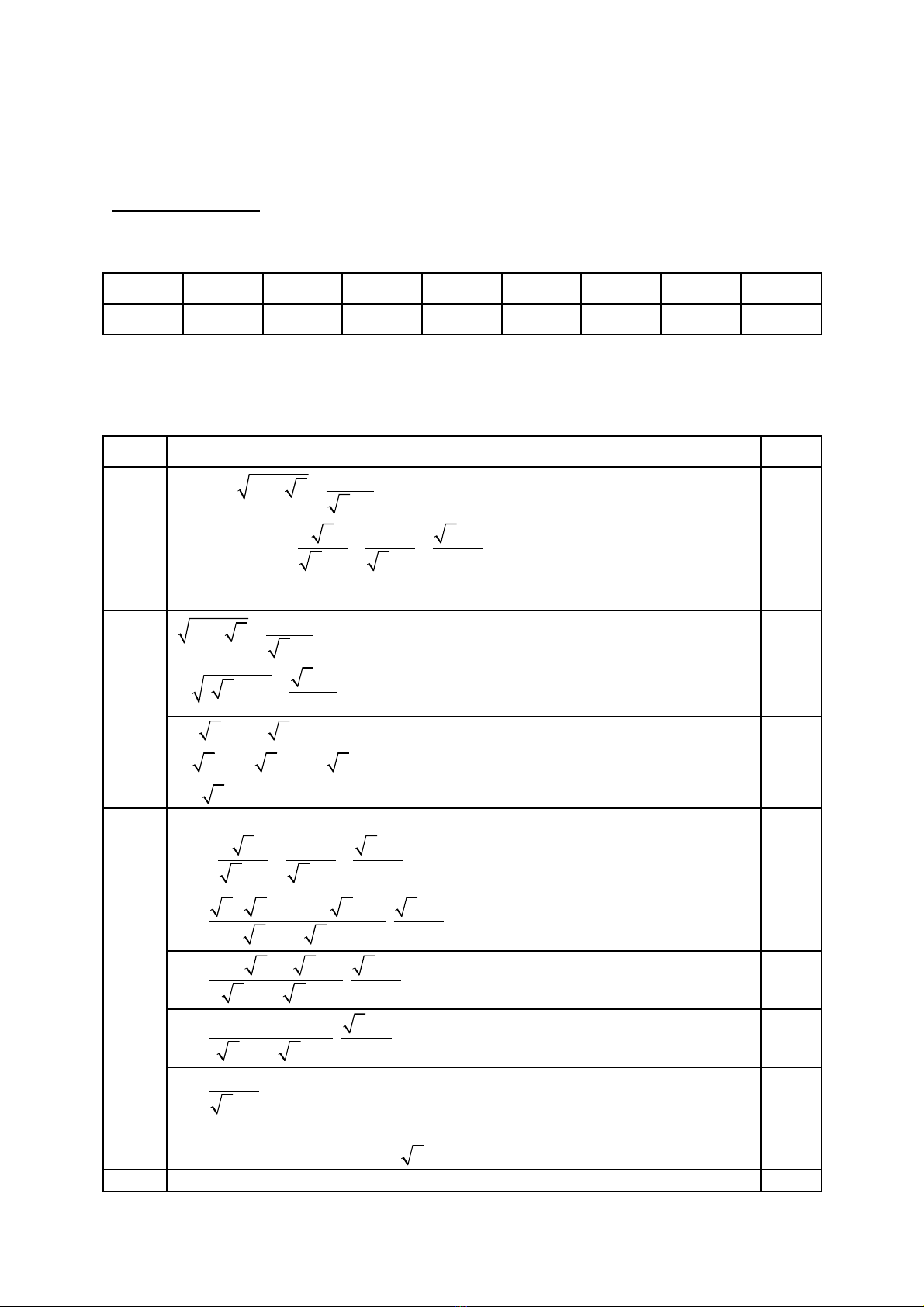
HƯỚNG DẪN CHẤM
Phâ'n tră(c nghiê*m: (2,0 điêm)
Môi đap an đung đươc 0,25 điêm
Câu 1 2 3 4 5 6 7 8
Đa#p a#n B A A D C B A D
Phâ'n tư* luâ*n: (8,0 điêm)
Nô*i dung Điê?m
Ba*i 1 1)Ti#nh:
1
3 2 2 2 1
+ + +
2)Ru#t go%n
3 3
.9
3 3
x x
Ax
x x
+
= +
+
+ −
vơ#i
0x
va*
9x
1,5
điêm
1)
(0,5
điêm)
2
1
3 2 2 2 1
2 1
( 2 1) 2 1
+ + +
−
= + + −
0,25
( 2 1) 2 1
2 1 2 1( 2 1 0)
2 2
vi
= + + −
= + + − − >
=
#
0,25
2)
(1,0
điêm)
Vơ#i
0x
;
9x
, ta co#:
3 3
.9
3 3
.( 3) 3( 3) 3
.9
( 3)( 3)
x x
Ax
x x
x x x x
Ax
x x
+
= +
+
+ −
− + + +
=+
+ −
0,25
3 3 9 3
.9
( 3)( 3)
x x x x
Ax
x x
− + + +
=+
+ −
0,25
9 3
.9
( 3)( 3)
x x
Ax
x x
+ +
=+
+ −
0,25
1
3
Ax
=−
Vâ%y vơ#i
0x
;
9x
thi*
1
3
Ax
=−
0,25
Ba*i 2
Cho ha*m sô#
2
3y kx k= − + +
(d)
1)Ti*m
k
đê đô* thi% ha*m sô# că#t tru%c hoa*nh ta%i điêm co# hoa*nh đô% la* 4
2)Ti*m
k
biê#t đô* thi% ha*m sô# (d) la* đươ*ng thăng song song vơ#i đươ*ng thăng
5 6y x= +
1,5
điêm
1)
(0,75
điêm)
Đô* thi% ha*m sô# (d) că#t tru%c hoa*nh ta%i điêm co# hoa*nh đô% la* 4 tư#c la* đô* thi% ha*m
sô# (d) đi qua điêm (4;0)
2
0 .4 3k k
= − + +
0,25
2
4 3 0
( 1)( 3) 0
k k
k k
− + =
− − =
1 0
3 0
k
k
− =
− =
1
3
k
k
=
=
0,25
Vâ%y
1k
=
;
3k
=
la* gia# tri% câ*n ti*m 0,25
2)
(0,75
điêm)
Đô* thi% ha*m sô# (d) la* đươ*ng thăng song song vơ#i đươ*ng thăng
5 6y x= +
2
5
3 6
k
k
− =
+
0,25
2
5
3
k
k
= −
5
3
k
k
= −
5k
= −
0,25
Vâ%y
5k
= −
la* gia# tri% câ*n ti*m 0,25
Ba*i 3 Cho hê% phương tri*nh:
1
2 4
mx y
x my
− = −
+ =
Ti*m tâ#t ca ca#c gia# tri% cua
m
đê hê% phương tri*nh co# nghiê%m duy nhâ#t
( ; )x y
thoa ma4n
2x y+ =
1,0
điêm
Tư* phương tri*nh
1mx y
− = −
(1), ta co#
1y mx= +
(*)
Thay (*) va*o phương tri*nh:
2 4x my
+ =
(2), ta co#:
0,25
0,25
0,25
0,25
Ba*i 4 Cho đươ*ng tro*n
( ; )O R
va* 1 điêm A nă*m ngoa*i đươ*ng tro*n. Tư* A ve4 2 tiê#p
tuyê#n AB va* AC (B,C la* tiê#p điêm). Ve4 đươ*ng ki#nh BD, đươ*ng thăng vuông
go#c vơ#i BD ta%i O că#t đươ*ng thăng DC ta%i E.
a) Chư#ng minh: DC//OA
b) Chư#ng minh: Tư# gia#c AEDO la* hi*nh bi*nh ha*nh
c) Đươ*ng thăng BC că#t OA va* OE lâ*n lươ%t ta%i I va* K
3
điêm
1đ Xét (O) có AB, AC là 2 tiếp tuyến cắt nhau tại A tại hai tiếp điểm B, C
ﾷ
=
=>
AB AC
AOla�pha�ngia�cBAC
0,25
Suy ra
∆
ABC cân tại A và phân giác AO đồng thời là đường trung trực của
BC
OA
⊥
BC
0,25
Xét (O) có
∆
BCD nội tiếp và cạnh BD là đường kính
∆
BCD vuông tại C
DC
⊥
BC
0,25
Do đó CD//OA 0,25
1đ Từ DC//OA
ﾷ
ﾷ
=BOA ODE
(hai góc đồng vị) 0,25
Xét (O) có AB là tiếp tuyến tại B
AB
⊥
OB 0,25
Xét
∆
OBA và
∆
DOE có
ﾷ
ﾷ
=BOA ODE
(cmt)
OB=OB (bán kính (O))
ﾷ
ﾷ
= =
0
OBA DOE 90
Do đó
∆
OBA =
∆
DOE (g.c.g) suy ra OA=DE
0,25
Xét tứ giác OAED có
OA//ED và OA=ED
Vậy tứ giác OAED là hình bình hành
0,25
1đ Xét
∆
OBA vuông tại O có BI
⊥
BA (I
OA)
IO.IA=IB2 (hệ thức cạnh và đường cao trong
∆
vuông ) (1)
0,25
Xét
∆
OBK vuông tại O có OI
⊥
BK (I
KB)
IK.IB=IO2 (hệ thức cạnh và đường cao trong
∆
vuông )
0,25
Vì OA là đường trung trực của BC (cmt)
IB=IC
Do đó OI2=IK.IC (2)
0,25
Xét
∆
OBI vuông tại I có
OI2+IB2=OB2 (định lý Pitago)
OI2+IB2=R2 (vì OB=R) (3)
Từ (1), (2) và (3) suy ra IO.IA+IK.IC=R2
0,25
Ba*i 5 Giai phương tri*nh:
2
2 2 ( 2) 3 2 0x x x x− − − + + =
1
điêm
ĐKXĐ:
2
3
x
−
2
2 2
2 2 ( 2) 3 2 0
( 3 2) (2 2 3 2) (3 2) 0
( 3 2) 2( 3 2) ( 3 2)( 3 2) 0
( 3 2)( 2 3 2) 0
( 3 2)(2 2 3 2) 0
3 2 0 (1)
2 2 3 2 0 (2)
x x x x
x x x x x x x
x x x x x x x x x
x x x x x
x x x x
x x
x x
− − − + + =
− + + − + + − + =
− + + − + + − + + + =
− + + + + + =
− + + + + =
− + =
+ + + =
+ Giai (1):