SỞ GIÁO DỤC ĐÀO TẠO HÀ TĨNH
TRƯỜNG THPT CẨM XUYÊN
KIỂM TRA GIỮA KỲ 1
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút;
(Đề có 4 trang)
Họ tên : .................................................................
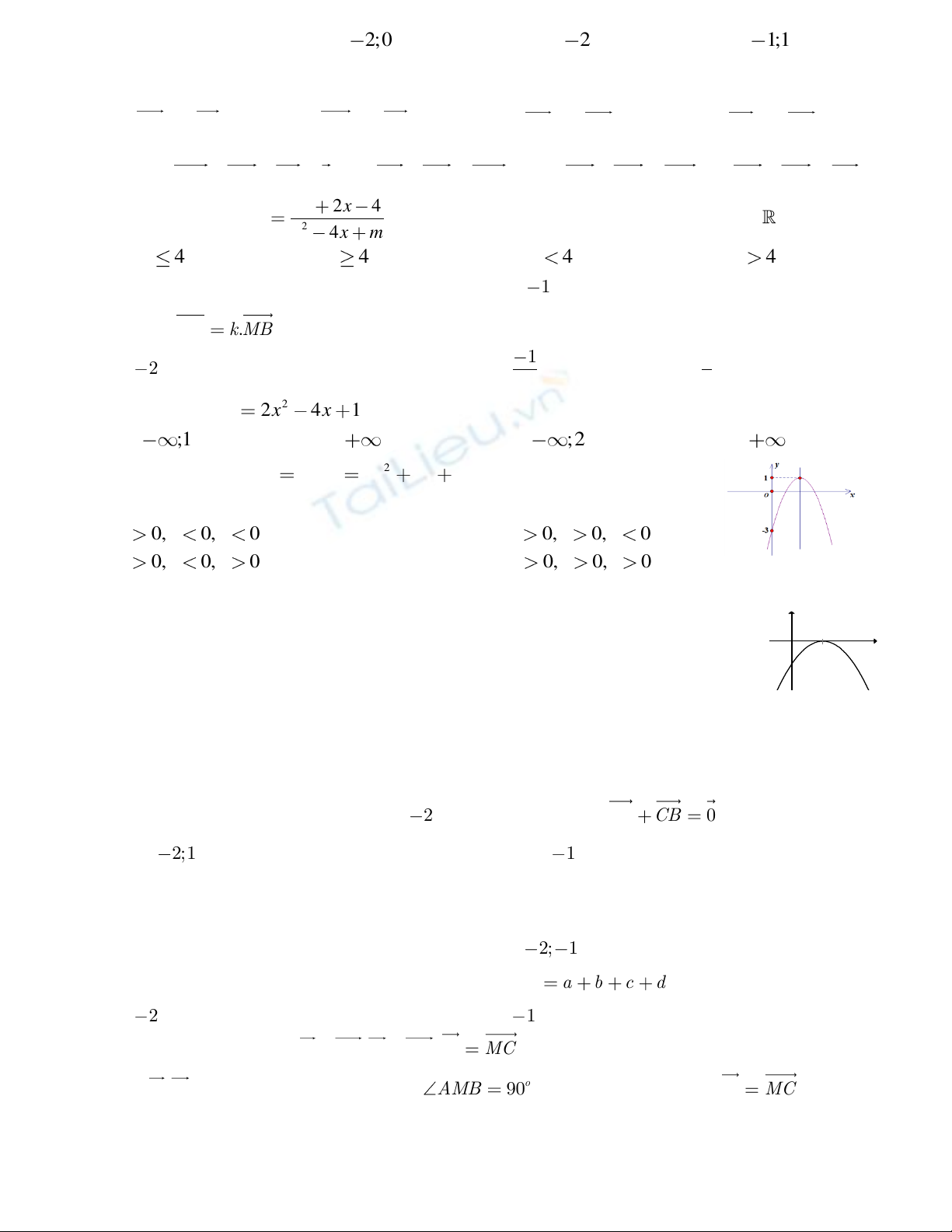
Câu 1: Đồ thị hàm số:
2
y ax bx c
như hình bên. Trong các hệ số a, b, c có bao
nhiêu giá trị dương?
A.
B.
0
C.
2
D.
3
Câu 2: Cho tam giác đều ABC, cạnh
3a
. Mệnh đề nào sau đây đúng:
A.
3AC a
B.
AC BC
C.
AB AC
D.
3AC a
Câu 3: Hoành độ đỉnh parabol
243y x x
là
A.
1x
B.
2x
C.
1x
D.
2x
Câu 4: Cho hai tập hợp
1;3;5;7 , 1;2;4;7AB
. Tìm giao của hai tập hợp
A
và
B
.
A.
2;4AB
B.
{1;7}AB
C.
1;2;3;4;5;7AB
D.
3;5AB
Câu 5: Tọa độ giao điểm của đồ thị hàm số
22y x x
với trục tung là
A.
0; 2
B.
2;0
C.
0;2Q
D.
1;0
Câu 6: Cho hai tập hợp
1;3;5;7 , 1;2;4;7AB
. Tìm hiệu của tập hợp
A
và
B
.
A.
\ 1;2;3;4;5;7AB
B.
\ 2;4AB
C.
\ {3;5}AB
D.
\ 1;7AB
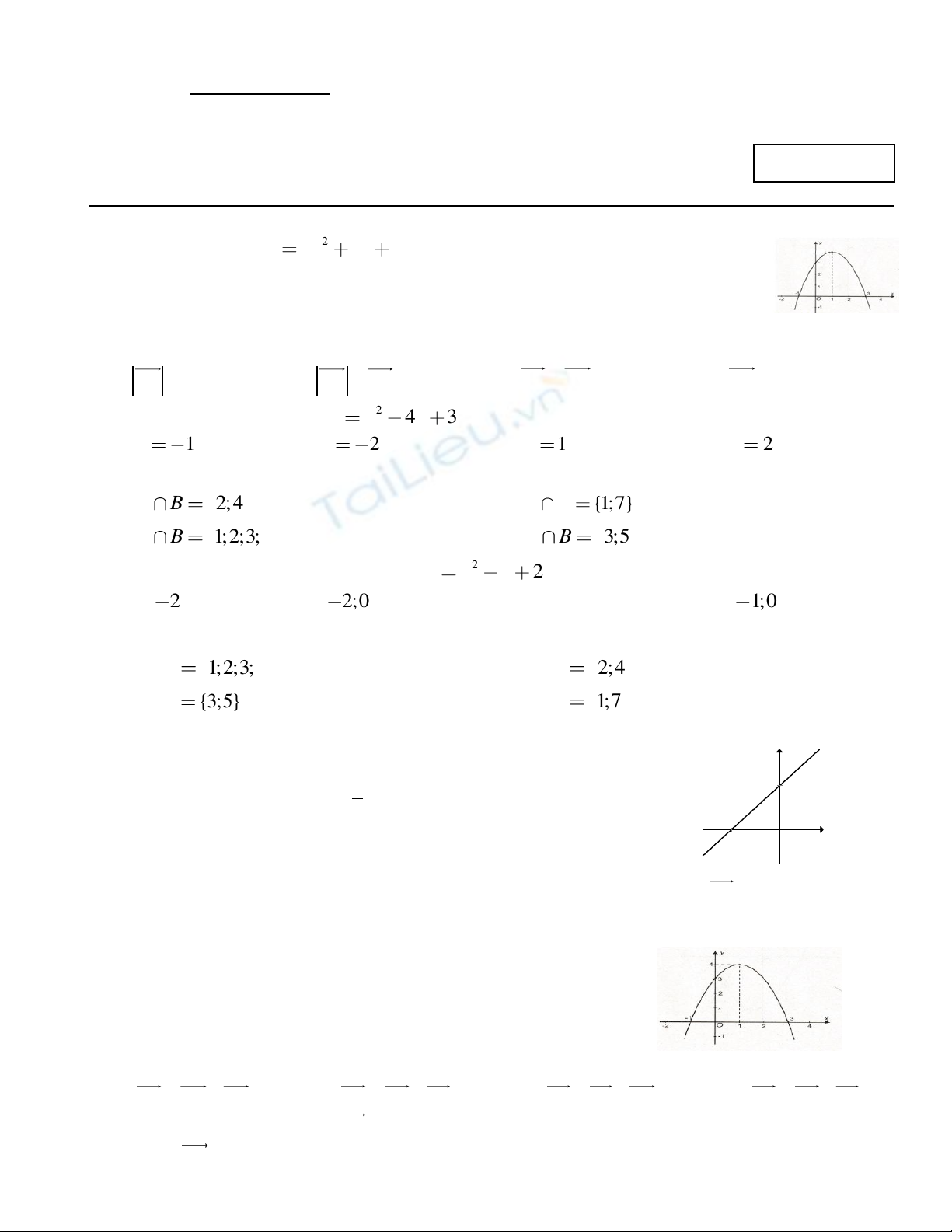
Câu 7: Cho hàm số có đồ thị là hình bên.
Tìm và
A. và . B. và
C. và . D. và .
Câu 8: Trong mặt phẳng tọa độ , cho , . Tìm tọa độ của véctơ .
A. . B. . C. . D. .
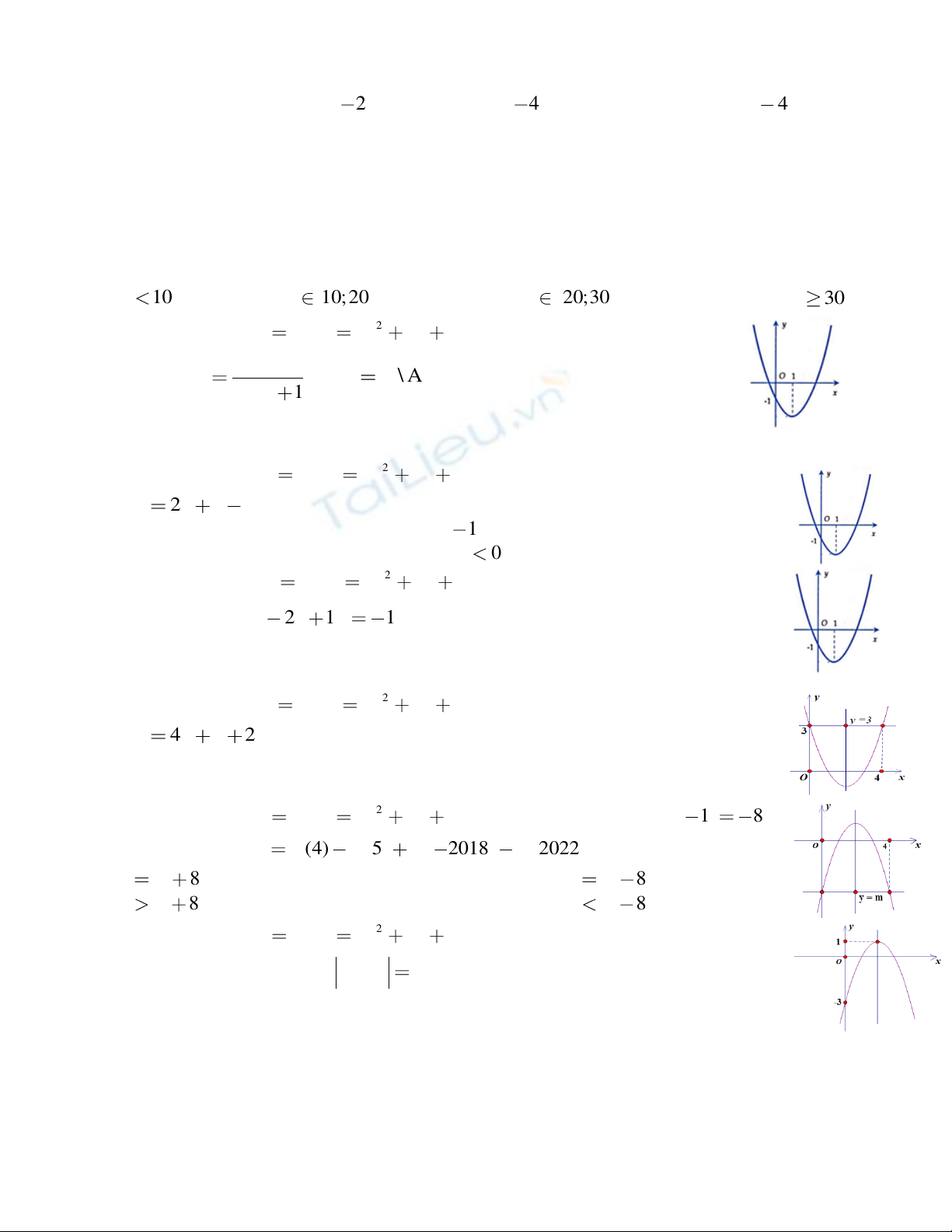
Câu 9: Hình bên là đồ thị của hàm số nào sau đây ?
A.
22 3.y x x
B.
22 3.y x x
C.
22 3.y x x
D.
22 3.y x x
Câu 10: Cho 4 điểm bất kỳ . Đẳng thức nào sau đây là đúng?
A. . B. . C. . D. .
Câu 11: Có bao nhiêu vectơ khác
0
có điểm đầu, điểm cuối là các đỉnh của hình bình hành
ABCD
cùng
phương với
AB
?
A.
4
B.
1
C.
3
D.
2
y ax b
a
.b
2a
3b
3
2
a
3b
3
2
a
2b
3a
3b
x
y
O
-2
Oxy
5;3A
7;8B
AB
15;10
2; 5
2;5
2;6
, , ,A B C O
AB AC BC
AB OB OA
OA CA CO
OA OB BA
Mã đề : 02
Câu 12: : Hàm số nào dưới đây là hàm số lẻ?
A.
2
21y x x
B.
42
5 7 3y x x
C.
3
26y x x
D.
43
5y x x
Câu 13: Đẳng thức nào dưới đây SAI?
A.
MN MP NP
B.
MN MP PN
C.
NM NP PM
D.
MN NP MP
Câu 14: Hàm số nào dưới đây nghịch biến trên ?
A.
32yx
B.
56yx
C.
2 1 1yx
D.
65yx
Câu 15: Cho vectơ
u
khác
0
. Vectơ nào dưới đây ngược hướng với
u
?
A.
3.u
B.
( 5 2).u
C.
3.u
D.
0,5.u
Câu 16: Trong hệ tọa độ Oxy, cho . Tọa độ trung điểm đoạn AB là:
A. B. C. D.
Câu 17: Cho tam giác có trọng tâm G, biết
1;2 ; 1; 2 ; 4; 3A B G
. Tọa độ điểm
C
là:
A.
2;1C
B.
2; 9C
C.
10;2C
D.
10; 9C
Câu 18: Cho tam giá
ABC
có trọng tâm
G
. Đẳng thức nào dưới đây đúng?
A.
0AG GB GC
B.
0GA GB GC
C.
0GA GB GC
D.
0GA GB GC
Câu 19: Hàm số nào sau đây đồng biến trên R:
A.
21yx
B.
2
y x x
C.
1yx
D.
1yx
Câu 20: Trong hệ tọa độ Oxy, cho điểm
2; 3A
. Hình chiếu vuông góc của A lên truc tung, trục hoành lần
lượt là
12
(a; b); (c; d)AA
. Giá trị của
T a b c d
là:
A.
3
B.
2
C.
1
D.
0
Câu 21: Tìm tham số
m
để hàm số
212y x m x m
đồng biến trên khoảng
1;
.
A.
3m
B.
3m
C.
3m
D.
3m
Câu 22: Tìm tham số
m
để hàm số
22 1 2y x m x m
nghịch biến trên khoảng
1;2
.
A.
1m
B.
1m
C.
0m
D.
0m
Câu 23: Cho tam giác
ABC
có
G
là trọng tâm,
I
là trung điểm
.BC
Đẳng thức nào đúng?
A.
1
3
IG IA
B.
2GA GI
C.
GB GC GA
D.
2GB GC GI
Câu 24: Tập xác định của hàm số
34
24

x
yxx
A.
[ 4; ) \ 2D 
B.
\2D
C.
( 4; ) \ 2D 
D.
D
Câu 25: Tìm
m
để hai đường thẳng
1: 2 3d y x
và
2
2: 2 1d y m x m
song song với nhau.
A. Không tồn tại
m
B.
2m
C.
2m
D.
2m
Câu 26: Cho hai hàm số
33f x x x
và
22021g x x
. Khi đó:
A.
fx
chẵn,
gx
lẻ B.
fx
lẻ,
gx
chẵn
C.
fx
và
gx
cùng lẻ D.
fx
lẻ,
gx
không chẵn không lẻ
Câu 27: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
242y x x
trên đoạn
[0;3]
.
Tính giá trị biểu thức
Mm
.
A.
1
B.
4
C.
0
D.
1
Câu 28: Điểm nào dưới đây thuộc đồ thị hàm số
32yx
?
(4;2), (10; 8)AB
6; 10
7; 3
6;10
14; 6
ABC
A.
2;4N
B.
2;0M
C.
3; 2Q
D.
1;1P
Câu 29: Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC. Hỏi cặp vectơ nào
sau đây cùng hướng?
A.
AN
và
CA
. B.
MN
và
CB
. C.
MA
và
MB
. D.
AB
và
MB
.
Câu 30: : Cho tam giác
ABC
, với
M
là trung điểm
BC
. Mệnh đề nào sau đây đúng?
A.
0AM MB BA
B.
AB AC AM
C.
MA MB MC
D.
MA MB AB
Câu 31: Cho hàm số
2
2
24
4
xx
yx x m
(
m
là tham số). Tìm
m
để hàm số xác định trên .
A.
4m
B.
4m
C.
4m
D.
4m
Câu 32: Trong hệ tọa độ Oxy, cho hai điểm
2; 3 ; 4; 1AB
.Giao điểm của đường thẳng AB với trục tung
tại
M
, đặt
.MA k MB
, giá trị của
k
là:
A.
2
B.
2
C.
1
2
D.
1
2
Câu 33: Hàm số
2
2 4 1y x x
nghịch biến trên khoảng nào dưới đây?
A.
;1
B.
2;
C.
;2
D.
1;
Câu 34: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Giá trị
của hệ số
,,abc
thỏa mãn:
A.
0, 0, 0a b c
B.
0, 0, 0abc
C.
0, 0, 0a b c
D.
0, 0, 0abc
Câu 35: Hàm số
y f x
có đồ thị như sau. Mệnh đề nào sau đây là mệnh đề SAI?
A. Hàm số đạt giá trị lớn nhất tại
1x
. B. Hàm số đồng biến trên
;1
.
C.
( ) 0f x x R
. D.
()f x m
có nghiệm khi và chỉ khi
0m
x
y
O
Câu 36: Hàm số
2 2 2
2 . 2 2 1y f x x m m x m m
. Mệnh đề nào sau đây là mệnh đề SAI?
A. Hàm số đạt giá trị lớn nhất trên
[ 1;0]
bằng
0f
. B. Hàm số nghịc biến biến trên
0;;
.
C. Hàm số đạt giá trị nhỏ nhất trên
[ 1;0]
bằng
1f
. D. Hàm số đồng biến trên
;0
.
Câu 37: Trong mp Oxy, cho
1;2 ; 5; 2AB
. Điểm
C
thỏa mãn:
30CA CB
, tọa độ điểm
C
là:
A.
2;1C
B.
2; 9C
C.
4; 1C
D.
2;1C
Câu 38: Trong hệ tọa độ Oxy, cho . Giá trị của m để ba điểm A, B, C
thẳng hàng là: A. B. C. D.
Câu 39: Trong hệ tọa độ Oxy, cho hai điểm
2; 3 ; 2; 1AB
.Giao điểm của đường thẳng AB với trục
tung, trục hoành lần lượt tại
(a; b); (c; d)MN
, giá trị của
T a b c d
là:
A.
2
B.
2
C.
1
D.
0
Câu 40: Giả sử có hai lực ,
3
F MC
cùng tác động vào một vật tại điểm Cường độ
hai lực lần lượt là
300N
,
400N
và
90o
AMB
. Tìm cường độ của lực
3
F MC
biết vật đứng
yên.
A.
700N
B.
250N
C.
500N
D.
1000N
1;2 , 2;5 2 , 3;4A m B m C m
1m
3m
2m
2m
12
, F MA F MB
.M
12
, FF
Câu 41: Đồ thị hàm số:
22y x x
cắt đường thẳng
22y m x
tại hai điểm phân biệt có hoành độ lần
lượt là
12
;xx
. Giá trị của
12
T x x
là:
A.
2
B.
2
C.
4
D.
24m
Câu 42: Số các giá trị nguyên dương của tham số
m
để đồ thị hàm
2y x m
cắt parabol
22y x x
tại
hai điểm phân biệt.
A.
2
B.
C.
4
D.
3
Câu 43: Cho đồ thị hàm số:
22
2 2 1y x mx m
cắt đồ thị hàm số:
2yx
tại hai điểm có hoành độ
lần lượt là
12
;xx
. Gọi
;Mm
là giá trị lớn nhất, nhỏ nhất của
22
1 2 1 2
.H x x x x
,giá trị
T M m
thỏa
mãn:
A.
10T
B.
10;20T
C.
20;30T
D.
30T
Câu 44: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Tập xác
định hàm số:
1
1
yfx
là
\ADR
, số phần tử của tập hợp A là:
A.
B.
0
C.
2
D.
3
Câu 45: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Giá trị của biểu
thức:
2T a b c
bằng:
A.
B.
1
C.
0
D.
0m
Câu 46: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Số nghiệm của
phương trình:
22 1 1f f x x
bằng:
A.
B.
2
C.
3
D.
4
Câu 47: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Giá trị của biểu
thức:
42T a b c
bằng:
A.
8
B.
6
C.
3
D.
4
Câu 48: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên và
18f
Giá trị của biểu thức:
(4) 5 2018 2022T f f f f
bằng:
A.
8Tm
B.
8Tm
C.
8Tm
D.
8Tm
Câu 49: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên. Số giá trị
nguyên của
m
để phương trình
2
f x m
có đúng 4 nghiệm phân biệt là:
A.
B.
2
C.
3
D.
4
Câu 50: Tìm tất cả các giá trị nguyên của tham số
m
để đồ thị hàm
2y m x
cắt parabol
22y x x
tại
hai điểm phân biệt cùng có hoành độ nhỏ hơn 1.
A.
7
B.
8
C.
9
D.
10
-------------------HẾT ------------------