Trang 1/5 - Mã đề 004
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG DÂN TỘC NỘI TRÚ
TỈNH
(Đề có 3 trang)
ĐỀ GIỮA KỲ I– NĂM HỌC 2023 - 2024
MÔN TOÁN - KHỐI LỚP 10
Thời gian làm bài : 90 Phút
Đề 01
Họ tên : ............................................................... Số báo danh : ...................
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A.
2 2
5x y
.B.
3 4 0x y z
.C.
2
2 0x y
. D.
2
2 2x y
.
Câu 2: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
A.
0
2 1
x y
x y
. B.
.
C.
3 0
2 5
x y z
x y
. D.
2 2
5 3
5 4
x y
x y
.
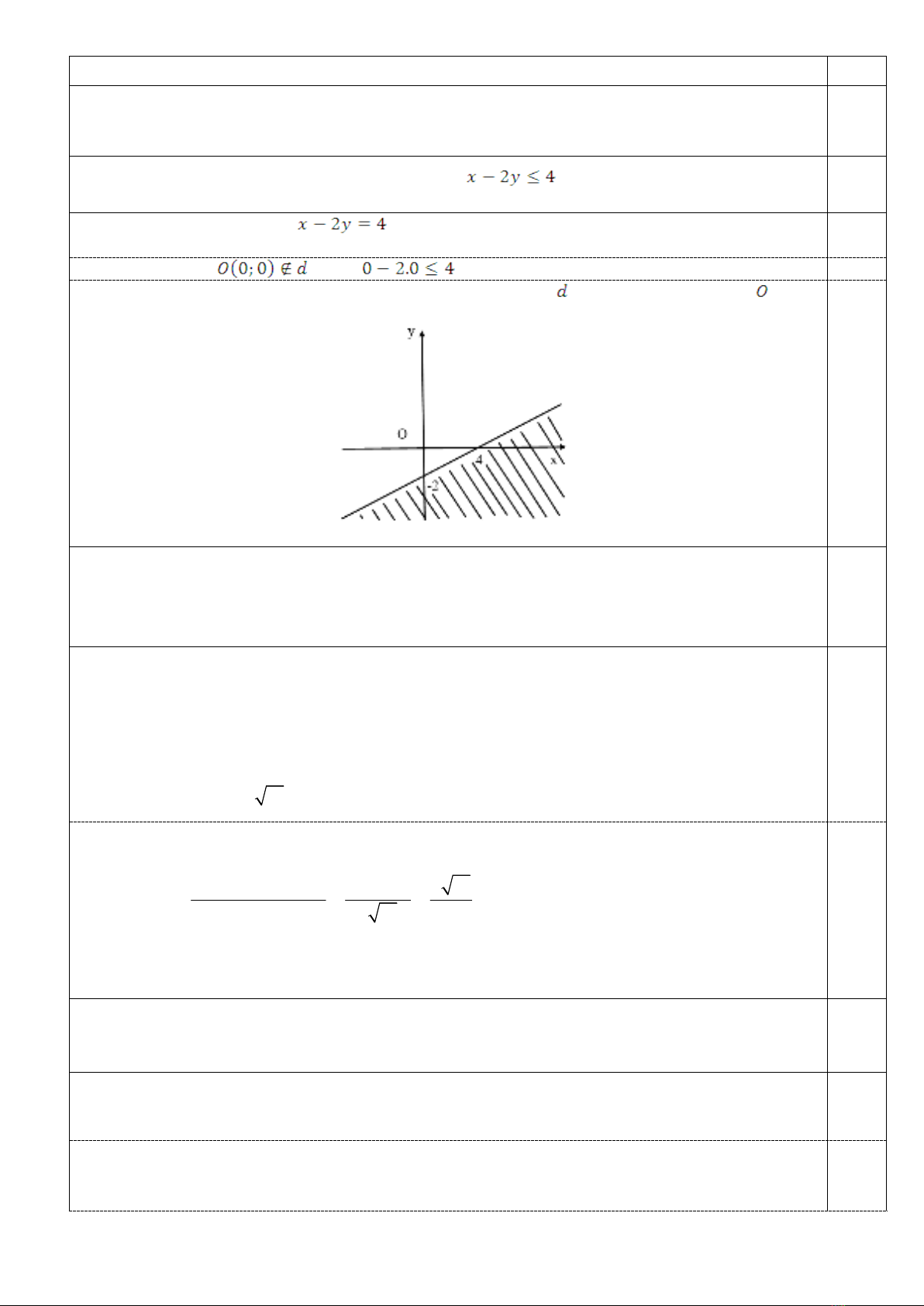
Câu 3: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình:
2 1
6 4
x y
x y
A. (0;1). B. (1;1) C. (-1;1) D. (-2;2)
Câu 4: Mệnh đề phủ định của mệnh đề “2023 là số tự nhiên lẻ” là
A. 2023 là số chính phương. B. 2023 không là số tự nhiên lẻ.
C. 2023 là số nguyên tố. D. 2023 là số lẻ.
Câu 5: Giá trị của
sin 45 cos 45
là
A.
2
2
. B. 1. C.
2 2
. D.
2
.
Câu 6: Cho tập hợp
|10 15A x N x
. Tập hợp
A
được viết dưới dạng liệt kê các phần tử là:
A.
11;12;13;14;15A
. B.
10;11;12;13;14;15A
.
C.
10;11;12;13;14A
. D.
11;12;13;14A
.
Câu 7: Cho tam giác
ABC
. Trong các hệ thức sau, hệ thức nào đúng?
A.
2 2 2 . .cosBC AB AC AB AC A
. B.
2 2 2
2 . .cosBC AB AC AB AC A
.
C.
2 2 2 2 . .cosAB CA CB CA CB C
. D.
2 2 2 2 . .cosAC BA BC BA BC A
.
Câu 8: Trong tam giác
ABC
gọi
R
là bán kính đường tròn ngoại tiếp tam giác. Trong các hệ thức
sau, hệ thức nào đúng?
A.
sin sin
BC AB R
A C
. B.
sin sin 2
A C R
BC AB
.
C.
sin AR
BC
. D.
2
sin
BC R
A
.
Câu 9: Cho tam giác
ABC
có độ dài ba cạnh là
, ,BC a AC b AB c
. Gọi
R
là bán kính đường
tròn ngoại tiếp tam giác và
S
là diện tích tam giác đó. Mệnh đề nào dưới đây đúng?
A.
abc
SR
. B.
4
abc
SR
. C.
4
R
Sabc
. D.
4
ac
SR
.
Câu 10: Cho
A
= {1; 3; 5}. Tập hợp nào sau đây là tập con của tập
A
?
A.
0
. B.
1;3;5;6
.
Trang 2/5 - Mã đề 004
C.
1;3
.D.
0;1;5
.
Câu 11: Trong các câu sau, câu nào không phải là một mệnh đề?
A. Số 19 là số lẻ phải không? B. Số 12 chia hết cho 5.
C. 17 là số nguyên tố. D. 25 là số chính phương.
Câu 12: Hình vẽ nào sau đây (phần không bị gạch) biểu diễn đoạn
[1;4]
?
A. B.
C. D.
Câu 13: Mệnh đề đảo của mệnh đề
P Q
là mệnh đề nào?
A.
Q P
. B.
Q P
. C.
Q P
. D.
Q P
.
Câu 14: Trong các đẳng thức sau đây, đẳng thức nào sai?
A.
tan 180 tan
90
. B.
cos 180 cos
.
C.
sin 180 sin
. D.
cot 180 cot
0 180
.
Câu 15: Miền nghiệm của hệ bất phương trình
1
2
1
x
x y
y
là:
A. Miền ngũ giác. B. Miền tứ giác.
C. Một nửa mặt phẳng.
D. Miền tam giác.
Câu 16: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình
nào trong bốn hệ A, B, C, D ?
A. .
1
4
y
x y
B. .
1
4
y
x y
C. .
1
4
y
x y
D. .
1
4
y
x y
Câu 17: Cho 2 tập hợp
5;0A
và
2;B 
. Mệnh đề nào sau đây đúng?
A.
2;0A B
. B.
5;A B 
.
C.
\ 5; 2A B
. D.
\ 0;B A
.
Câu 18: Với giá trị thực nào của
x
mệnh đề chứa biến
2
:3 2 0P x x
là mệnh đề đúng:
A.
2.x
B.
0x
. C.
1x
D.
1x
.
Câu 19: Trong các câu sau, câu nào là một mệnh đề chứa biến?
A. Số 9 là số nguyên tố B. 12 +2=1 5.
Trang 3/5 - Mã đề 004
C.
2 6.x
. D.
là số hữu tỉ
. Câu 20: Cho tập hợp
1;5 , 1;3;5X Y
. Tập
X Y
là tập hợp nào sau đây?
A.
1
B.
1;3
C.
{1;3;5}
D.
1;5
Câu 21: Trong các đẳng thức sau đây, đẳng thức nào đúng?
A.
3
sin150 2
°=-
.B.
tan150 3°=
.C.
1
cos150 2
°=
.D.
cot150 3°=-
.
Câu 22: Cho góc
a
thỏa mãn
0 180
a
°£ £ °
. Khẳng định nào sau đây đúng?
A.
sin 1
a
>
.B.
0 sin 1
a
£ £
.
C.
0 cos 1
a
£ £
.D.
cos 1
a
<-
.
Câu 23: Cho
ABC
vuông tại
A
, góc
B
bằng
30
. Khẳng định nào sau đây là sai?
A.
cos 3
2
B
.B.
3
sin 2
C
.C.
cos 2
2
C
.D.
1
sin 2
B
Câu 24 : Tính diện tích tam giác
ABC
biết
3, 5, 6AB BC CA
.
A.
2 14
B.
4 3
.C.
6
.D.
8
.
Câu 25: Cho tam giác
ABC
có góc
60BAC
và cạnh
3BC
. Tính bán kính của đường tròn
ngoại tiếp tam giác
ABC
.
A.
4R
.B.
1R
.C.
2R
.D.
3R
.
PHẦN CÂU HỎI TỰ LUẬN
Câu 1: (1,0 điểm). Tìm phủ định các mệnh đề sau:
a)
:A
“ Hà Nội là thủ đô của Việt Nam”.
b)
B:
2
" , 0"3 1xx x
Câu 2:(1,0 điểm). Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
Câu 3: (1 điểm) .Cho tam giác
ABC
có
3BC
,
1BA
,
120B
.
a) Tính độ dài cạnh
AC
.
b) Tính số đo góc
C
(làm tròn đến phút).
Câu 4: (1 điểm). Lớp 10A1 có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh
giỏi cả môn Toán và Lý, 6 học sinh không giỏi môn nào trong cả hai môn nói trên. Hỏi lớp 10A1 có
bao nhiêu học sinh?
Câu 5: (1,0 điểm). Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất140 kg chất A và
9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và
0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A
và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít
nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I
và không quá 9 tấn loại II.
------ HẾT ------
.
ĐÁP ÁN PHẦN TỰ LUẬN
Đáp án
Điểm
Câu 1. Phủ định các mệnh đề sau:
a) “ Hà Nội là thủ đô của Việt Nam”.
Trang 4/5 - Mã đề 004
b)
2
" , 0"3 1xx x
.
a) “ Hà Nội không phải là thủ đô của Việt Nam”,
b)
2
" , 0"3 1xx x
1,0 đ
Câu 2.Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
1,0
điểm
Bước 1: Vẽ đường thẳng (d):
Đường thẳng đi qua hai điểm (0; -2) và (4;0)
0,25
Bước 2: Lấy điểm , ta có:
0,25
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng bờ (tính cả d ) chứa điểm (miền
không bị gạch)
0,5
Câu 3: (1 điểm) Cho tam giác
ABC
có
3BC
,
1BA
,
120B
.
a) Tính độ dài cạnh
AC
.
b) Tính số đo góc
C
(làm tròn đến phút).
1,0
điểm
a) Tính độ dài cạnh
AC
.
Gợi ý làm bài:
Áp dụng định lí côsin cho tam giác
ABC
, ta có:
2 2 2 0
2 .BC.c os120AC AB BC AB
2 2 0
1 3 2.1.3.c os120 13
Vậy
13AC
0,5
b) Tính số đo góc
C
.
Gợi ý làm bài:
Ta có
2 2 13 9 1 7 13
cosC= 2. .BC 26
6 13
AC BC AB
AC
.
Vậy
13 54'C
.
0,5
Câu 4: (1 điểm) Lớp 10A1 có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học
sinh giỏi cả môn Toán và Lý, 6 học sinh không giỏi môn nào trong cả hai môn nói trên. Hỏi
lớp 10A1 có bao nhiêu học sinh?
1,0
điểm
Số học sinh giỏi Toán là: 25-14 =11(học sinh).
Số học sinh giỏi Lý là : 23-14 =9(học sinh).
0,25
Số học sinh giỏi cả hai môn là: 14 (học sinh).
Số học sinh không giỏi môn nào trong cả hai môn là: 6(học sinh).
0,25
Trang 5/5 - Mã đề 004
Vậy số học sinh lớp 10A1 là: 11+9+14+6 = 40(học sinh).
0,5
Câu 30(1,0 điểm). Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất140 kg chất A
và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A
và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất
A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu
là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu
loại I và không quá 9 tấn loại II.
1,0
điểm
Gọi x(tấn) nguyên liệu loại I và y(tấn) nguyên liệu loại II dùng để chiết xuất ra ít nhất 140 kg chất
A và 9 kg chất B ( Đk: ).
Theo giả thiết , có thể chiết xuất được (20x+10y) kg chất A và (0,6x+1,5y) kg chất B
Theo bài ra ta có hệ bất phương trình:
0,25
Trên hệ trục tọa độ , vẽ các đường thẳng
.
Ta có miền nghiệm của hệ bất phương trình là miền trong tứ giác và kể cả tứ giác ABCD
(phần không bị gạch).
Ta có: A , B , C và D .
0,5
Số tiền mua nguyên liệu là (triệu đồng)
Ta lại có: , ; ,
Suy ra, đạt giá trị nhỏ nhất khi .
Vậy cần dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chiết xuất ít nhất140 kg chất
A và 9 kg chất B với chi phí 32 triệu .
0,25