Trang 1/3 - Mã đề 122
SỞ GD & ĐT QUẢNG NAM
TRƯỜNG THPT HÙNG VƯƠNG
KIỂM TRA CUỐI HỌC KỲ I - NĂM HỌC 2024 - 2025
MÔN: TOÁN 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐỀ CHÍNH THỨC
(Đề có 3 trang)
Họ tên : ............................................................... Số báo danh : ...................
PHẦN I. (5,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 15.
Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1: Cho hình lập phương
.ABCD A B C D
. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
AB AD AA AC
+ + =
. B.
.
C.
AB AC AA AC

+ + =
. D.
AC AD AA AC

+ + =
.
Câu 2: Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con nai và thu được kết quả như sau:
Nhóm chứa tứ phân vị thứ ba là
A.
[16;17)
. B.
[17;18)
. C.
[15;16)
. D.
[18;19)
.
Câu 3: Xét mẫu số liệu ghép nhóm có phương sai bằng
64
. Độ lệch chuẩn của mẫu số liệu đó bằng
A.
256
. B.
32
. C.
8
. D.
4
.
Câu 4: Mỗi ngày anh Hùng đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: km) của
anh Hùng trong 20 ngày được thống kê lại ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm là
A. 1,5. B. 0,9. C. 0,3. D. 0,8.
Câu 5: Trong không gian với hệ tọa độ
,Oxyz
cho tam giác
ABC
có trọng tâm
( )
3;1;4G−
và
( ) ( )
1;0; 1 , 2;3;5AB−
. Tọa độ điểm
C
là
A.
( )
6;2;0C−
. B.
( )
3; 1; 5 .C−−
C.
( )
4;2; 1 .C−
D.
( )
12;0;8 .C−
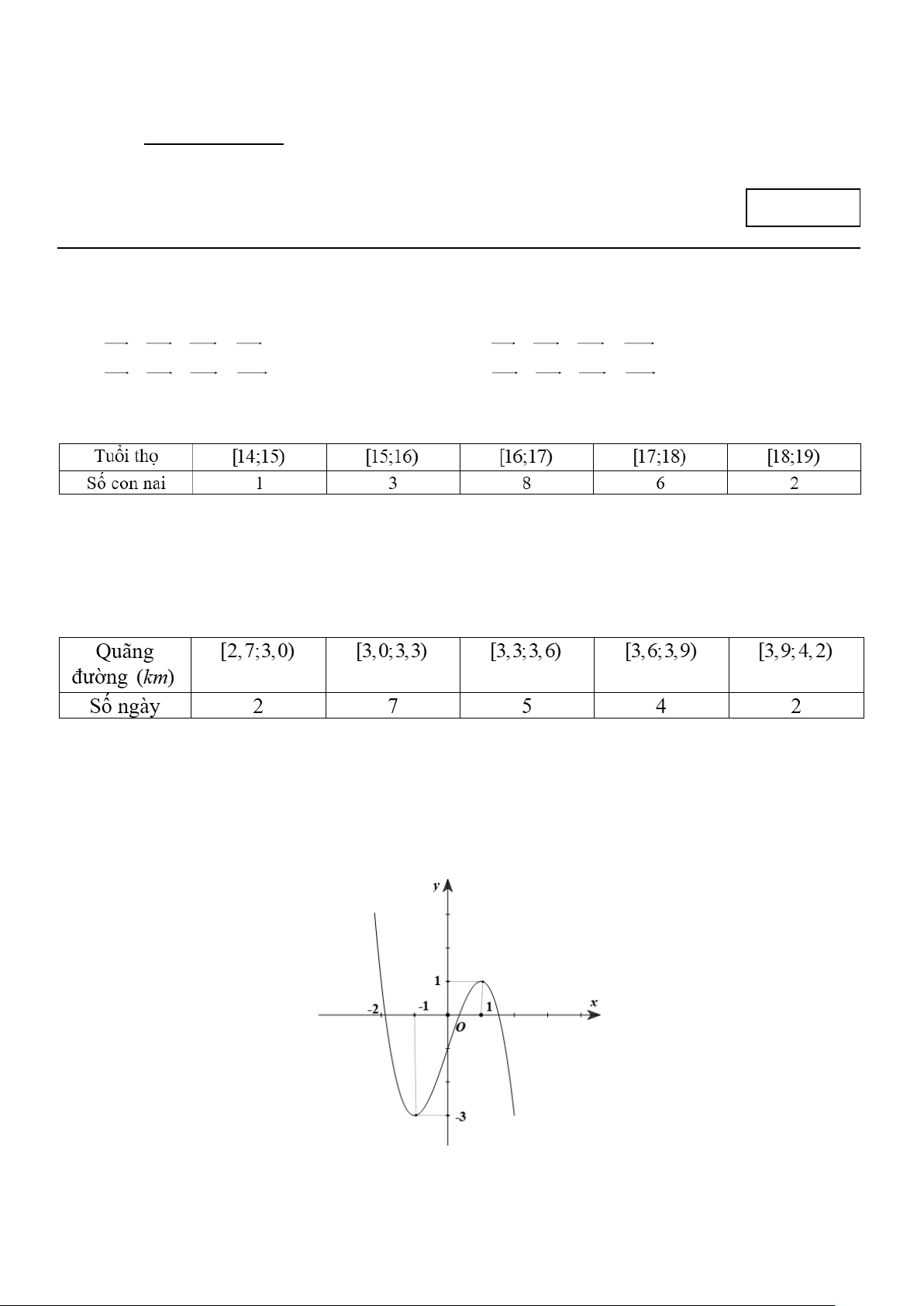
Câu 6: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây
A.
331y x x= − −
. B.
331y x x= − + −
. C.
42
1y x x= − + −
. D.
31y x x= − + −
.
Câu 7: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Mã đề 122
Trang 2/3 - Mã đề 122
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A.
( 1;1).−
B.
( )
;1 .−
C.
( )
1; .− +
D.
( )
3; 1 .−−
Câu 8: Giá trị nhỏ nhất của hàm số
( )
321f x x x=−
trên đoạn
2;19
bằng
A.
14 7−
. B.
34−
. C.
36−
. D.
14 7
.
Câu 9: Tìm tiệm cận xiên của đồ thị hàm số
222
1
xx
yx
+−
=−
.
A.
1yx=+
. B.
3yx=+
. C.
1y=
. D.
2yx=+
.
Câu 10: Trong không gian
Oxyz
với hệ tọa độ
( )
; ; ;O i j k
cho
2 5 .OA j i k= − +
Tìm tọa độ điểm
A
.
A.
( )
5; 2;1A−
. B.
( )
2;1;5A−
. C.
( )
2;5;1A−
. D.
( )
1; 2;5A−
.
Câu 11: Trong không gian với hệ tọa độ
,Oxyz
hình chiếu vuông góc của điểm
( )
3;2;1M−
trên mặt phẳng
( )
Oxz
có tọa độ là
A.
( )
3; 2;1−−
. B.
( )
3;2;0−
. C.
( )
0;2;1
. D.
( )
3;0;1−
.
Câu 12: Trong các khẳng định sau, khẳng định nào sai?
A. Phương sai luôn luôn là số không âm.
B. Phương sai là bình phương của độ lệch chuẩn.
C. Phương sai luôn luôn lớn hơn độ lệch chuẩn.
D. Phương sai càng lớn thì độ phân tán của các giá trị quanh số trung bình càng lớn.
Câu 13: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2
1 4 ,f x x x x x
= + −
. Số điểm cực trị của hàm số đã
cho là
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 14: Trong không gian với hệ tọa độ
,Oxyz
cho ba điểm
( )
4;1; 5A−−
;
( )
2; 4;7B−
;
( )
3; 2;9C−
. Tọa độ
điểm
D
sao cho tứ giác
ACBD
là hình bình hành là
A.
( )
2;3; 3D−
. B.
( )
3;3; 3D−−
. C.
( )
3; 3;3D−−
. D.
( )
5; 1; 7D− − −
.
Câu 15: Cho tứ diện
ABCD
. Gọi
G
là trọng tâm của tam giác
BCD
. Khẳng định nào sau đây là đúng?
A.
2AB AC AD AG+ − =
. B.
3AB AC AD AG+ + = −
.
C.
2AB AC AD AG+ + =
. D.
3AB AC AD AG+ + =
.
Trang 3/3 - Mã đề 122
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b),
c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số
221
2
xx
yx
− + −
=+
A. Hàm số đồng biến trên khoảng
( )
5;1−
B. Giá trị lớn nhất của hàm số trên
( )
2;− +
bằng
0.
C. Đồ thị hàm số có tiệm cận đứng là
2.x=
D. Đồ thị hàm số đi qua điểm
( )
1;2
.
Câu 2: Trong không gian
Oxyz
, cho hình bình hành
ABCD
. Biết
( ) ( ) ( )
1;1;2 , 1;0;3 , 1;2; 2A B C −
.
A. Trọng tâm
G
của tam giác
ABC
có tọa độ là
( )
1;1;1G
.
B. Vectơ
2BC i j k= − +
.
C. Tọa độ điểm
D
là
( )
2;3; 3D−
.
D. Góc
ABC
là góc tù
PHẦN III. (1,0 điểm) Trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 2.
Câu 1. Một công ty tiến hành khai thác 14 giếng dầu trong khu vực được chỉ định. Trung bình mỗi giếng
dầu chiết xuất được 138 thùng dầu mỗi ngày. Công ty có thể khai thác nhiều hơn 14 giếng dầu nhưng cứ
khai thác thêm một giếng thì lượng dầu mỗi giếng chiết xuất được hằng ngày sẽ giảm 8 thùng. Để công ty có
thể quyết định số giếng cần thêm cho phù hợp với tài chính, hãy chỉ ra số giếng công ty có thể khai thác
thêm để sản lượng dầu chiết xuất đạt lớn nhất.
Câu 2. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo là kilômét, một máy bay chiến đấu di
chuyển với vận tốc và hướng không đổi từ điểm
(55;126;10)A
đến điểm
(201;238;4)D
trong 30 phút. Nếu
máy bay tiếp tục giữ nguyên vận tốc và hướng bay sau phút tiếp theo thì tọa độ của máy bay lúc này là
( ; ; )P a b c
. Kết quả của phép tính
2025
abc++
(làm tròn đến hàng phần mười) bằng bao nhiêu?
PHẦN IV. (2,0 điểm) Tự luận.
Câu 1. Tìm giá trị lớn nhất của hàm số
2
( ) 2024 2y f x x x= = −
.
Câu 2. Trong không gian Oxyz, cho tam giác ABC có
(2; 1;3)A−
,
(1;2; 1)B−
,
( 4;7;5)C−
. Gọi D là điểm
thuộc cạnh BC sao cho D cách đều hai đường thẳng AB và AC. Tính độ dài đoạn thẳng AD.
==== HẾT ====
(Giám thị không giải thích gì thêm!)