MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I, TOÁN 9
Năm học: 2024 – 2025
Thời gian làm bài: 90 phút
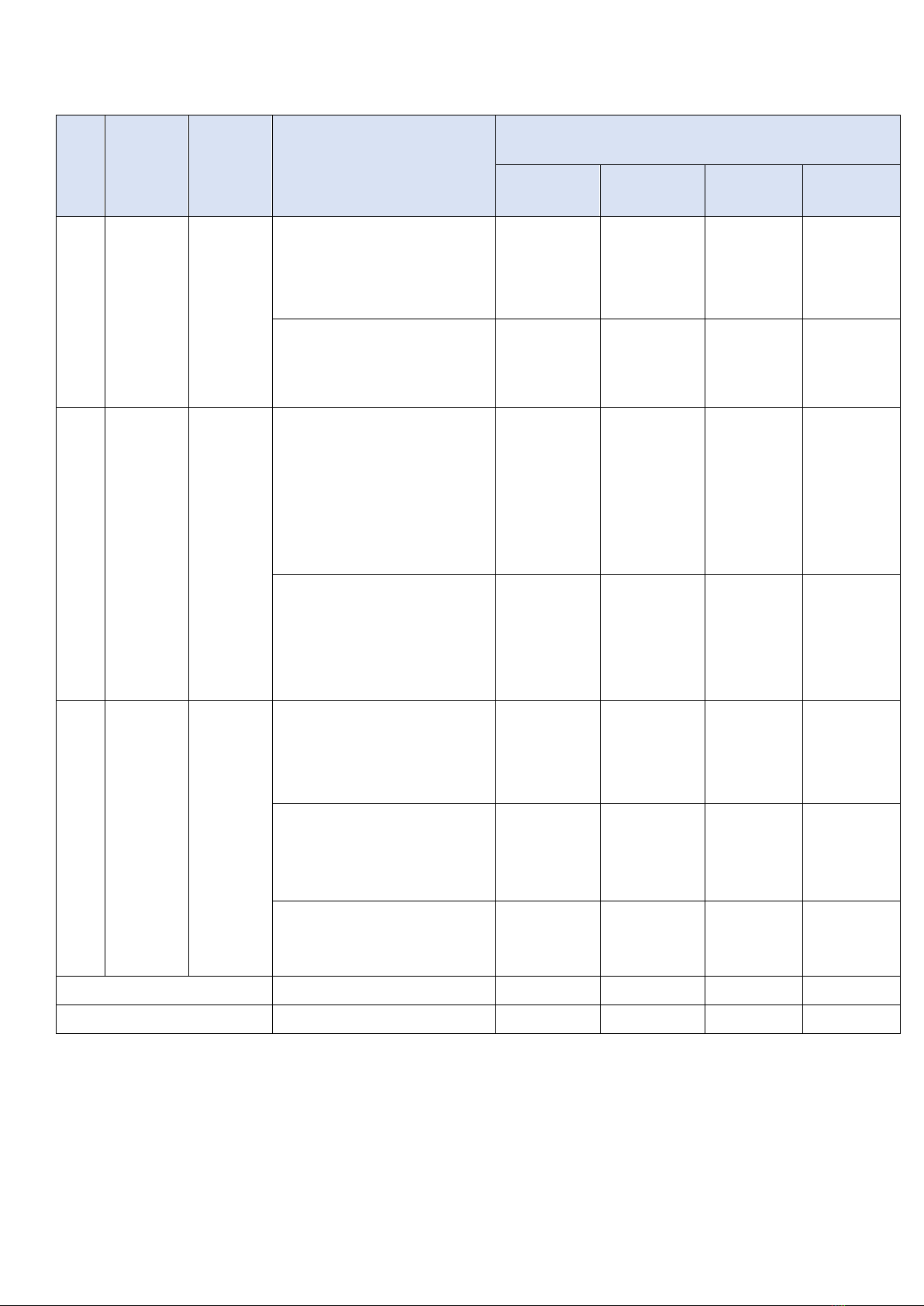
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Tổng
Bất đẳng thức
Bất phương
trình bậc nhất
- Nhận biết được BĐT, mô tả được một số tính chất cơ bản
của BĐT
- Bài toán nâng cao về bất đẳng thức
- Giải bất phương trình bậc nhất một ẩn
1
1,0
1
0,5
3
2,5
Căn thức
- Định nghĩa, ĐKXĐ, các tính chất của phép khai phương
- Tính và biến đổi đơn giản biểu thức chứa căn thức bậc
hai, bậc ba
Số câu
Số điểm
3
2,5
1
0,5
5
4,0
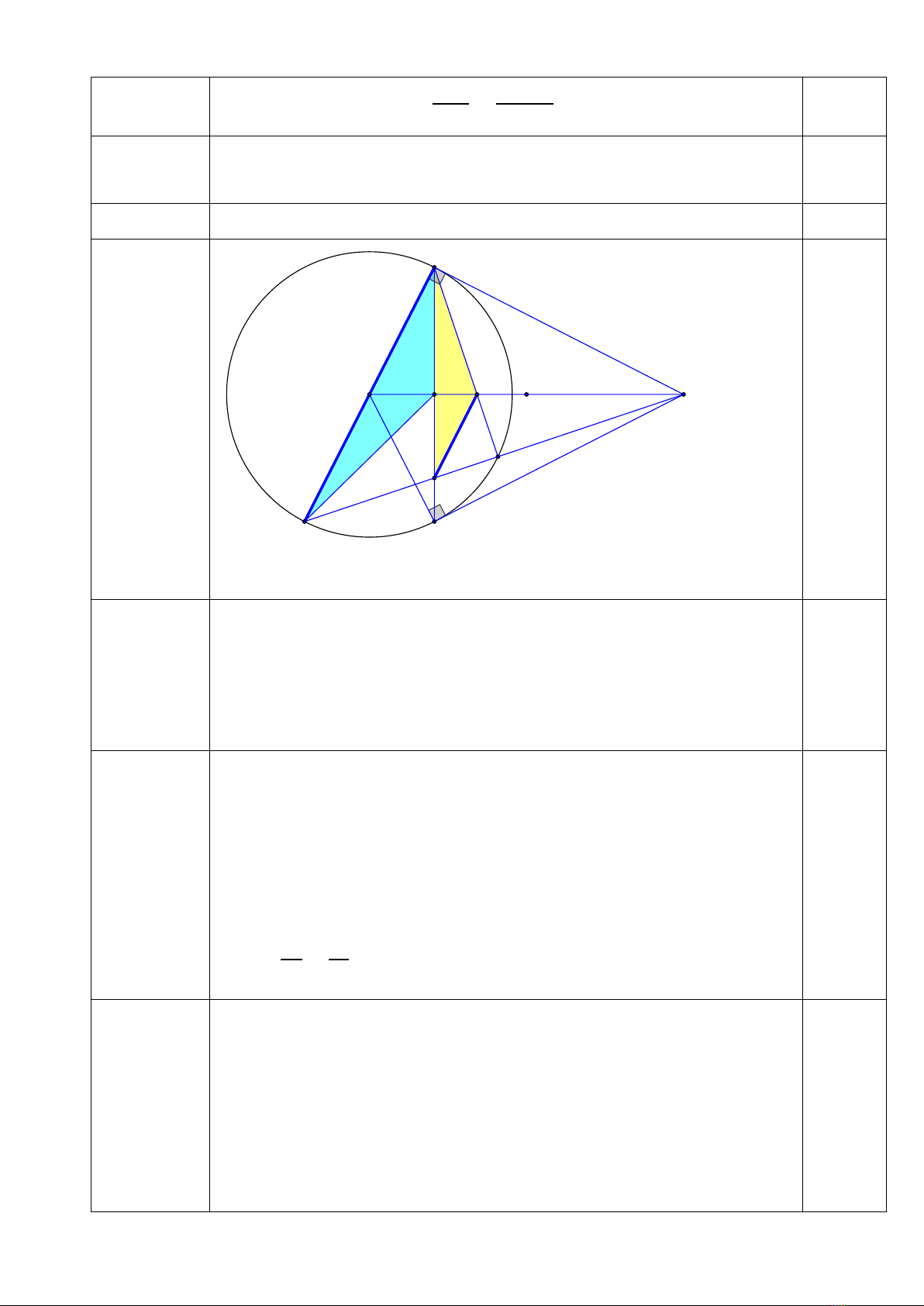
Đường tròn
- Định nghĩa, tính chất của góc ở tâm, góc nội tiếp số đo cung.
- Sử dụng tính chất tiếp tuyến, góc nội tiếp, góc ở tâm
- Độ dài cung tròn, diện tích hình quạt tròn, hình vành
khăn
Số câu
Số điểm
3
1,5
1
0,5
1
0,5
6
3,5
Tổng số câu
Số điểm
6
4,0
3
2,0
2
1,0
14
10
Tỉ lệ %
40%
20%
10%
100%
Ký duyệt của tổ chuyên môn Phước Bửu, ngày 11/12/2024
Tổ trưởng Nhóm trưởng
(Đã ký) (Đã ký)
Lưu Quang Diện Nguyễn Thị Tính
BẢNG ĐẶC TẢ ĐỀ KIỂM TRA HK 1, MÔN TOÁN 9, NĂM HỌC 2024 – 2025
TT
Chương
Nội
dung
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Vận dụng
cao
1
Bất
đẳng
thức
Bất
phương
trình
bậc
nhất
- Nhận biết được bất PT
bậc nhất 1 ẩn
- Nhận biết nghiệm của
bất phương trình.
- Giải bất phương trình.
- Bài toán nâng cao về
BĐT
Bài 2b
(TL-1,0đ)
Bài 2c
(TL-1,0đ)
Bài 5
(TL-0,5đ)
2
Căn
thức
Căn bậc
hai, căn
bậc ba.
Biến
đổi đơn
giản và
rút gọn
căn
thức
bậc hai
- Hiểu được cách tìm điều
kiện của căn thức bậc hai.
- Hiểu được định nghĩa
căn bậc ba để tính giá trị
biểu thức số với căn bậc
ba
Bài 1a,b
(TL-1,5đ)
Bài 2a
(TL-1,0đ)
- Sử dụng được các kiến
thức về phép biến đổi căn
thức bậc hai để rút gọn
được biểu thức chứa căn
bậc hai.
Bài 1c
(TL-1,0đ)
Bài 1d
(TL-0,5đ)
3
Đường
tròn.
Nhận biết góc ở tâm, góc
nội tiếp của đường tròn
Tính góc ở tâm, góc nội
tiếp của đường tròn
Nhận biết: công thức tính
độ dài dây cung, diện tích
hình quạt tròn, hình vành
khuyên.
Bài 3ab
(TL-1,0đ)
Vận dụng: Tính chất tiếp
tuyến của đường tròn
chứng minh hình học
V hình
0,5đ
Bài 4a
(TL-1,0đ)
Bài 4b
(TL-0,5đ)
Bài 4c
(TL-0,5đ)
Số câu
6
3
3
2
Số điểm
4,0
3,0
2,0
1,0
Ký duyệt của tổ chuyên môn Phước Bửu, ngày 6/12/2024
Tổ trưởng Nhóm trưởng
Lưu Quang Diện Nguyễn Thị Tính
TRƯỜNG THCS PHƯỚC BỬU ĐỀ KIỂM TRA HỌC KỲ 1
TỔ TOÁN - TIN MÔN: TOÁN 9
NĂM HỌC 2024 – 2025
ĐỀ CHẴN Thời gian làm bài 90 phút (không kể thời gian giao đề)
(Đề này gồm 1 trang) Kiểm tra, ngày 3 tháng 1 năm 2025
Bài 1 (3 điểm). Rút gọn các biểu thức sau
a)√27
3+√16 b)√(√7−2)2+√(√7+2)2
c) 5
√7−√2−√10−√2
√5−1 d) √49𝑎−√72−𝑎√16
𝑎+√32 𝑣ớ𝑖 𝑎 >0
Bài 2 (3,0 điểm). Giải phương trình và các bất phương trình sau :
a) √𝑥−6 = 3 b) 3x + 7 > 10
c)
2𝑥+1
3≥𝑥−2
4
Bài 3 (1,0 điểm).
a) Tính độ dài cung 500 của một đường tròn có bán kính 8cm
b) Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn ( O; 9 cm) và (O; 12 cm)
Bài 4 (2,5 điểm).
Từ điểm A ở ngoài đường tròn (O), v hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai
tiếp điểm). Gọi H là giao điểm của BC và OA. V đường kính BM của đường tròn (O).
a/ Chứng minh OA BC
b/ Gọi N là giao điểm của AM với (O). Chứng minh : AM.AN = AB2
c/ Gọi E là giao điểm của MA và BC, I là giao điểm của AO và BN.
Chứng minh : EI.HM = BI.BH
Bài 5 (0,5 điểm). Cho a ≥ 1; b ≥ 1. Chứng minh : 𝑎√𝑏−1+𝑏√𝑎−1 ≤ 𝑎𝑏
----- Hết -----
Họ và tên học sinh ......................................................................
Chữ ký giám thị ..........................................................................
TRƯỜNG THCS PHƯỚC BỬU KIỂM TRA HỌC KỲ I, TOÁN 9
TỔ TOÁN – TIN NĂM HỌC 2024 - 2025
HƯỚNG DẪN CHẤM ĐỀ CHẴN (gồm 3 trang)
Hướng dẫn
Điểm
Bài 1(3đ)
a
(1 đ )
a)√27
3+√16 = 3 + 4 = 7
1,0
b
( 0,5 đ )
b)√(√7−2)2+√(√7+2)2
= |√7−2|+|√7+2|
= √7 − 2 + √7+2 = 2√7
0,25
0,25
c
( 1 đ )
d
(0,5 đ )
c) 5
√7−√2−√10−√2
√5−1 = 5(√7+√2)
5−√2(√5−1)
√5−1
= √7+√2−√2 = √7
d) √49𝑎−√72−𝑎√16
𝑎+√32 𝑣ớ𝑖 𝑎 > 0
=7√𝑎−6√2−4√𝑎+4√2 = 3√𝑎−2√2
0,5
0,25x2
0,25 x2
Bài 2(3,0đ)
a) √𝑥−6 = 3 ( đk : x ≥ 6 )
√𝑥−6 =√9
𝑥− 6 = 9
𝑥 = 15
0,25
0,25 x 3
b) 3x + 7 > 10
3x > 3
x> 1
vậy nghiệm của bpt là x > 1
0,5
0,5
𝑐)2𝑥+1
3≥𝑥−2
4
4(2𝑥+1)
12 ≥3(𝑥−2)
12
8𝑥+4 ≥ 3𝑥 −6
5𝑥 ≥ −10
𝑥 ≥−2
Vậy nghiệm của bpt là x ≥ -2
0,25
Bài 3 (1,0đ)
a
Độ dài cung 500 của một đường tròn có bán kính 8cm
0,5
𝑙 = 𝜋𝑅𝑛
180 =𝜋.8.50
180 ≈ 6,98
b
Diện tích hình vành khuyên giới hạn bởi hai đường tròn ( O; 9 cm) và
(O; 12 cm) là S = 𝜋.(122−92 ) ≈ 197,92
0,5
Bài 4 (2,5đ)
a
Hs v hình đến câu a được 0,5 đ
0,5
a
Ta có: AB = AC (tc 2tt cắt nhau )
OB = OC (bán kính)
Do đó: OA là đường trung trực của BC
Suy ra: OA
BC tại H
0,25x2
0,25x2
b
Xét ∆ANB và ∆ABM, ta có:
𝐴𝑁𝐵
= 𝐴𝐵𝑀
=900
𝐵𝐴𝑁
là góc chung
Vậy ∆ANB ∽ ∆ABM (g.g)
Suy ra: 𝐴𝑀
𝐴𝐵 =𝐴𝐵
𝐴𝑁
suy ra: AB2 = AM.AN
0,25
0,25
c
Xét ∆BEA có:
AH và BN là đường cao, AH cắt BN tại I
Suy ra: I là trực tâm của ∆BEA
Suy ra: EI
AB
Mà BM
AB nên EI // BM
Chứng minh: ∆OHB ∽ ∆OBA (g.g)
0,25
I
E
N
M
H
C
B
S
O
A