S GIÁO D C VÀ ĐÀO T O TP.H CHÍ MINHỞ Ụ Ạ Ồ
TR NG THPT PHÚ NHU NƯỜ Ậ
Đ THI H C KÌ II – NĂM H C: 201Ề Ọ Ọ 3 – 2014
Môn: Toán – Kh i 12ố
Th i gian làm bài: 120 phút ờ
A . PH N CHUNG CHO T T C H C SINH: Ầ Ấ Ả Ọ (7 đi m)ể
Câu 1: (3,5đ) Cho hàm s : ố
2 1
1
x
yx
−
=−
có đ th (C)ồ ị
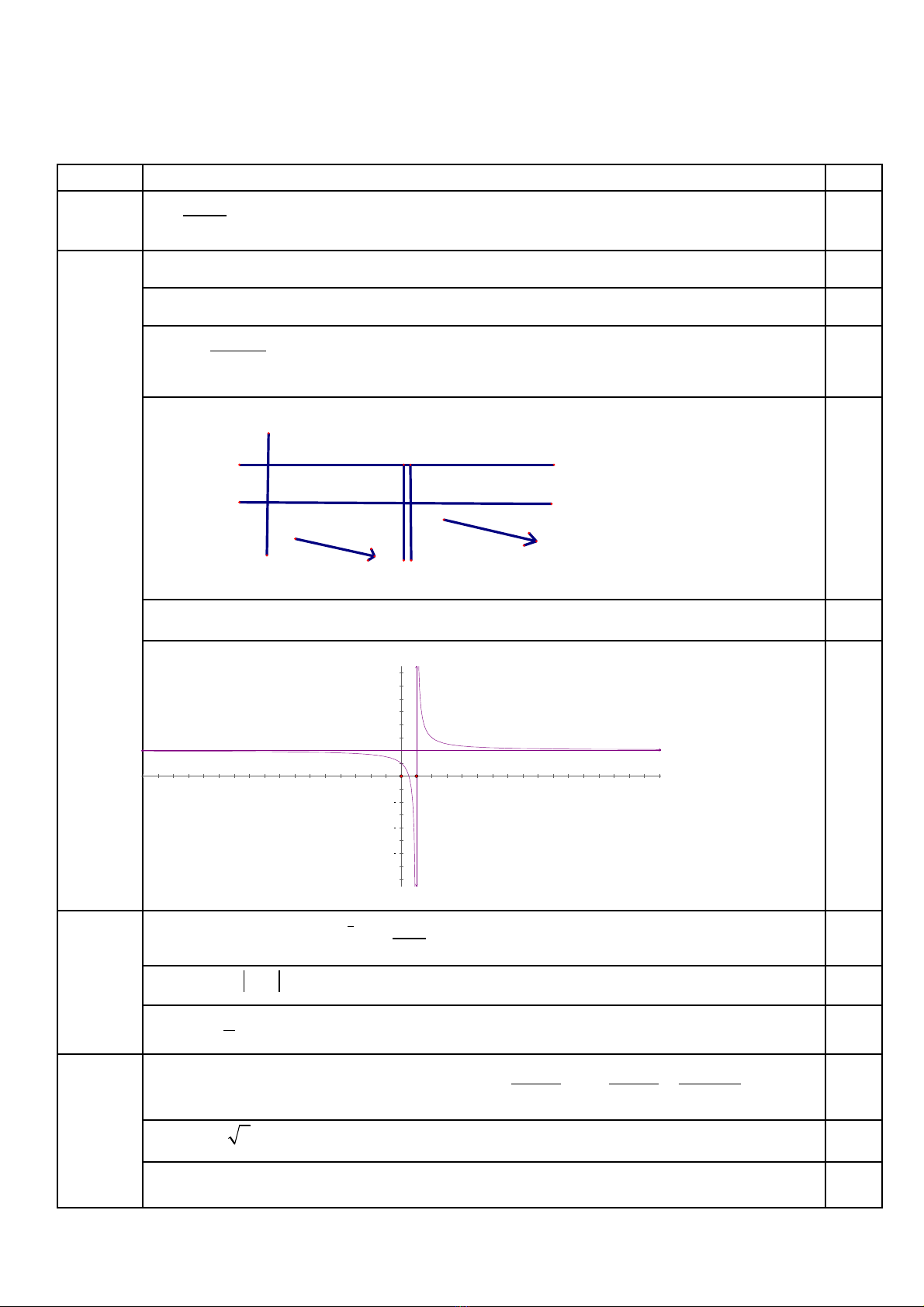
a) Kh o sát và v đ th (C).ả ẽ ồ ị
b) Tính di n tích hình ph ng gi i h n b i (C) và hai tr c t a đ.ệ ẳ ớ ạ ở ụ ọ ộ
c) Tìm đi m M thu c (C) sao cho kho ng cách t đi m A(1 ; 2) đn ti p tuy n v i ể ộ ả ừ ể ế ế ế ớ
đ th (C) t i M b ng ồ ị ạ ằ
2
Câu 2: (1,5đ) Tính các tích phân sau:
a)
4
0
I x cos 2xdx
π
=
b)
1
ln
. 1 ln
e
x
I dx
x x
=+
Câu 3: (2đ) Trong không gian Oxyz ,cho hai đng th ngườ ẳ
1 2
1 1 2 2
1 2
23 8 3 2
: 10 4 , : 2 2
x t x t
d y t d y t
z t z t
= − + = +
� �
� �
= − + = − −
� �
� �
= =
� �
a) Vi t ph ng trình m t ph ng (P) ch a dế ươ ặ ẳ ứ 1 và song song v i dớ2. Tính d(d1,d2).
b) Vi t ph ng trình đng th ng ế ươ ườ ẳ song song v i Oz và c t c hai đng th ng dớ ắ ả ườ ẳ 1, d2
B . PH N RIÊNG: Ầ(3 đi m)ể
H c sinh ch đc làm m t trong hai ph n ( Ph n I hay ph n II)ọ ỉ ượ ộ ầ ầ ầ
I Theo ch ng trình chu nươ ẩ
Câu 1: ( 2đ)
a) Gi i ph ng trình trên t p s ph c: zả ươ ậ ố ứ 2 – 4iz + 5 = 0
b) Tìm s ph c z th a ố ứ ỏ
z 5
=
và (z + i)2 là s thu n oố ầ ả
Câu 2: (1đ)
Trong không gian Oxyz, cho b n đi m ố ể
( )
A 1, 0, 2
,
( )
B 3, 2,1−
,
,
( )
D 2,0,0−
,
vi t ph ng trình ế ươ m t cặ ầu qua C, D và có tâm n m trên đng th ng AB.ằ ườ ẳ
II Theo ch ng trình nâng caoươ
Câu 1: (2đ)
a) Tìm ph n th c và ph n o c a s ph c z th a: ầ ự ầ ả ủ ố ứ ỏ
2 i
z 2i 1
3 2i
+
= + −
−
.
b) Tìm s ph c z bi t ố ứ ế
( )
( )
z 1 z 2i
− +
là s th c và ố ự
z
nh nh t ỏ ấ
Câu 2: (1đ) Trong không gian v i h tr c Oxyz cho đng th ngớ ệ ụ ườ ẳ (d) :
x 1 y z 2
121
+ −
= =
.
Tìm kho ng cách tả ừ đi m I(0, 0, 3)ể đn (d). Suy ra ế ph ng trìnhươ m t c u ặ ầ (S) tâm I, bi t (S) ế
c t d t i 2 đi m M, N ắ ạ ể th a ỏ
ﾷ
0
MIN 90
=
–------- H t ế–-------
Đáp án toán 12 – HK2 - 2014
A PH N CHUNGẦ7Đ
Câu 1
3,5đ
2 1
1
x
yx
−
=−
1a) 2đ
{ }
\ 1D R=
0.25
x
lim y 2
=
suy ra TCN y = 2 ;
x 1 x 1
lim y , lim y
+ −
= + = −
suy ra TCĐ x = 1 0.25
( )
2
1
' 0
1
y
x
−
= <
−
0.25
B ng bi n thiên ả ế
0.5
Hàm s ngh ch bi n trên (–ố ị ế ; 1) và (1 ; +∞)0.25
Đ th : (C) c t Ox t i (1/2 ; 0) , Oy t i (0 ; 1)ồ ị ắ ạ ạ
0.5
1b)
0,75đNhìn đ th ta có ồ ị
1
2
0
1
21
S dx
x
� �
= +
� �
−
� �
0.25
S =
1/2
0
(2 ln 1) |x x+ −
0.25
S =
1
1 ln 2
+
0.25
1c)
0,75đPh ng trình ti p tuy n (d) v i (C) t i ươ ế ế ớ ạ
( ) ( )
0 0
0 0
2
0 0 0
2 1 2 1 1
; :
1 1 1
x x
M x y x x
x x x
� �
− − −
− = −
� �
− − −
� �
0.25
( ) ( )
2
0
, 2 1 1d I x∆ = − =�
0.25
Tìm đc Mượ 1
(2 ; 3) , M
2
(0 ; 1) 0.25
8
6
4
2
2
4
6
8
15
10
5
5
10
15
2
2
-
-
y
y'
x
-
∞
+
∞
+
∞
-
∞
1
Câu 2a
(0.75đ) Đt ặ
du dx
u x
1
dv cos 2xdx v sin 2x
2
=
=
� �
==
0.25
4 4
4
0
0 0
1 1
I x cos 2xdx x sin 2x sin 2xdx
2 2
π π
π
= = −
� �
0.25
4 4
0 0
1 1 1
I x sin 2x cos 2x
2 4 8 4
π π
π
= + = −
0.25
Câu 2b
(0.75đ)
1
ln
. 1 ln
e
x
I dx
x x
=+
.Đt ặ
1 ln 2
dx
t x tdt
x
= + =�
0.25
I =
( )
23
2 2
1
1
2 1 2 |
3
t
t dt t
� �
− = −
� �
� �
0.25
4 2 2
3 3
I= −
0.25
Câu3a
1đMp (P) ch a dứ1 và song song d2 nên (P) có VTPT là
1 2
, (6; 6; 24)n u u
� �
= = − −
� �
r r r
0.25
Tìm đc pt mp(P): x – y – 4z + 13 = 0ượ 0.25
d(d1;d2) = d(M,(P))
18 3 2
18
= =
, (M(3;-2;0)d2) 0. 5
Câu3b
1đG i (P) là mp đi qua dọ1 và song song Oz nên (P) có VTPT là
1 1
; (1; 2;0)n u k
� �
= = −
� �
ur ur r
(P) : x – 2y + 3 = 0 0.5
G i A là giao đi m c a dọ ể ủ 2 và (P) suy ra
1 4 5
; ;
3 3 3
A� �
− −
� �
� �
0.25
Khi đó : qua A ,VTCP
( )
0;0;1k=
r
( )
1/ 3
4 / 3
5 / 3
x
y
z t
= −
∆ =
= − +
0.25
Chú ý : n u hs ếchỉ tìm đc VTCP Δ : (0 ;0 ;1) cho 0,25
Cách 2 : Δ c t dắ1 , d2 t i Mạ1, M2 . đk
1 2
M M
uuuuuur
cùng ph ng ươ
k
r
tìm đc M1 , M2 . cho thang
đi m t ng ngể ươ ứ
B PH N RIÊNG C B NẦ Ơ Ả
Câu 1a
1đ
x2 -4ix + 5 = 0 : = - 36 = 36i20. 5
Ch n căn b c 2 c a Δ là 6i . Khi đó ọ ậ ủ
5x i
x i
=
= −
0. 5
Câu 1b
1đ
a) z = a + bi (a, b ﾷ)
(z + i)2 = [a + (b + 1)i]2 = a2 – (b + 1)2 + 2a(b + 1)i 0.25
2
z 5
(z i) thuan ao
=
+
2 2
2 2
a b 5
a (b 1) 0
+ =
− + =
0. 25
a 2 a 1
b 1 b 2
= =
� �
� �
� �
= = −
� �
0. 25
V yậ
{ }
z 2 i, 2 i,1 2i, 1 2i
+ − + − − −�
0. 25
Câu 2
1đG i I là tâm m t c u c n tìm. ọ ặ ầ ầ
( )
AB 4, 2, 1= − −
uuur
x 1 4t
AB : y 2t
z 2 t
= −
=�= −
,
( )
I AB I 1 4t, 2t, 2 t− −� �
0.25
Do m t c u qua C và D nên ặ ầ
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
IC ID 2 4t 1 2t 2 t 3 4t 2t 2 t= + + − + − = − + + −�
0.25
1 5 2 17
36t 4 0 t I , ,
9 9 9 9
� �
− = =� � � � �
� �
2 2
274
R ID 27
= =�
0.25
V y m t c u c n tìm: ậ ặ ầ ầ
( )
2 2 2
5 2 17 274
S : x y z
9 9 9 27
� � � � � �
− + − + − =
� � � � � �
� � � � � �
0.25
B PH N RIÊNG NÂNG CAOẦ
Câu 1a
1đ.
( ) ( ) ( )
2 i 3 2i
2 i
z 2i 1 1 2i
3 2i 9 4
+ +
+
= + − = + − −
− +
0. 5
4 7 9 19
i 1 2i i
13 13 13 13
= + − − = − −
0.25
V y ph n th c c a z là: ậ ầ ự ủ
9
13
−
, ph n o c a z là ầ ả ủ
19
13
−
0.25
Câu 1b
1đG i z = a +bi Ta có ọ
( )
( )
( ) ( )
[ ]
z 1 z 2i a a 1 b b 2 ab (a 1)(b 2) i
− + = − + − + − − −
0.25
Mà
( )
( )
z 1 z 2i
− +
là s th c nên ố ự
ab (a 1)(b 2) 0 b 2 2a
− − − = = −�
0.25
( )
2
2
2 2
4 4 5
z a 2 2a 5a 8a 4 5 a 2
5 5 5
� �
= + − = − + = − +
� �
� �
0.25
z
nh nh t khi ỏ ấ
4 2 4 2
a ;b z i
5 5 5 5
= = = +�
0.25
Câu 2
1đVTCP
d
u (1, 2,1)
=
uur
. Ch n A( -1 ; 0 ; 2) thu c d ọ ộ
( ) ( )
1;0; 1 , 2;0; 2
d
AI AI u
� �
= − − = −�� �
uur uur uur
0.25
( )
( )
,2 3
,3
d
d
AI u
d I d
u
� �
� �
= =
uur uur
uur
0.25
MIN vuông cân t i I ạ MHI vuông cân t i Hạ (H trung đi m M , N)ể
Nên bán kính m t c u ặ ầ
2 2
R IM IH 2 3
= = =
0.25
Pt m t c u: ặ ầ
2 2 2
8
x y (z 3) 3
+ + − =
0.25