Trường THCS và THPT Đinh Thiện Lý
Năm học 2024 – 2025
ĐỀ THAM KHẢO KIỂM TRA TẬP TRUNG CUỐI HK2 MÔN TOÁN 8
Thời gian: 90 phút
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Câu 1: Trong mặt phẳng Oxy như hình vẽ, tọa độ điểm A là:
A.
( )
3; 2A−
B.
( )
2;3A−
C.
( )
3;2A−
D.
( )
3;2A
Câu 2: Đường thẳng
25yx=−+
có hệ số góc là:
A.
5
B.
2
C.
2x−
D.
2−
Câu 3: Đường thẳng
31yx= +
song song với đường thẳng nào dưới đây:
A.
B.
21yx= +
C.
31yx= −
D.
31yx=−−
Câu 4: Điểm nào dưới đây thuộc đồ thị hàm số
23yx= +
:
A.
( )
0; 3M−
B.
( )
1; 5N
C.
( )
1; 2P−
D.
( )
3; 0A
Câu 5: Lan có một giá sách với 10 quyển sách. Mỗi tuần Lan mua thêm 3 quyển sách mới. Gọi y là số sách
Lan có sau x tuần. Hàm số y theo biến x là :
A.
3yx=
B.
10yx=
C.
10yx= +
D.
3 10yx= +
Câu 6: Cho tam giác ABC có MN song song với BC như hình bên.
Chọn phát biểu đúng:
A.
AM AN MN
MB NC BC
= =
B.
AM AN MN
AB AC BC
= =
C.
AM AN BC
AB NC MN
= =
D.
MB NC MN
AB AC BC
= =
Câu 7: Cho tam giác ABC có I, K lần lượt là trung điểm của AB và AC. Chọn phát biểu đúng:
A. IK // BC và
1
2
IK AC=
B. IK // AC và
1
2
IK AC=
C. IK // BC và
1
2
IK BC=
D. IK // BC và
1
3
IK BC=
Câu 8: Cho tam giác ABC có số đo các cạnh và BJ là đường phân giác như hình
bên. Tính giá trị của x.
A.
3x=
B.
1.92x=
C.
3.5x=
D.
2.6x=
Câu 9: Gieo một con xúc sắc cân đối và đồng chất. Các kết quả thuận lợi để xuất hiện mặt có sô chấm nhỏ
hơn 3 là:
A.
{ }
1
B.
{ }
1; 2
C.
{ }
1; 2; 3
D.
{ }
2;3
Câu 10: Một hộp có 30 quả bóng xanh và 20 quả bóng đỏ. Chọn ngẫu nhiên 1 quả bóng từ hộp. Biết rằng
mỗi quả bóng có khả năng được chọn như nhau. Xác suất để chọn được quả bóng màu xanh là:
A.
2
3
B.
2
5
C.
3
5
D.
1
50
PHẦN II. TỰ LUẬN (8,0 điểm)
Câu 1 (1,5 điểm): Giải các phương trình sau:
a.
( ) ( )
−
−− =
35
22 5
2
x
x
b.
( )
( )
( )
− − + ++ =−
322
2 1 8 4 1 20 85x xx x
Câu 2: (0,5 điểm): Xác định hàm số, biết đồ thị của nó là đường thẳng
d
song song với đường thẳng
': 3 6dy x−=
và đi qua điểm
( )
1; 5A
.
Câu 3: (1,0 điểm) Xe I khởi hành từ A đến B. Sau đó 1 giờ 30 phút, trên cùng tuyến đường đó xe II khởi
hành từ B đi về A với vận tốc lớn hơn vận tốc xe I 5km/h. Sau khi xe I đi được 3 giờ 30 phút thì hai xe gặp
nhau. Tính vận tốc mỗi xe biết rằng quãng đường AB dài 175 km.
Câu 4: (1,5 điểm) Bác Tuấn gửi tiết kiệm một số tiền tại ngân hàng theo thể thức kì hạn một năm với lãi suất
4,8%/năm, tiền lãi sau mỗi năm sẽ gộp vào với tiền gốc để tính lãi cho năm tiếp theo. Sau hai năm, bác Tuấn
rút hết tiền về và nhận được cả vốn lẫn lãi là 549 152 000 đồng. Hỏi số tiền ban đầu bác Tuấn gửi tiết kiệm
là bao nhiêu?
Câu 5: (1,0 điểm) Cho tam giác ABC cân tại B có
9BA BC= =
,
4AC =
, đường phân giác của góc
BAC
cắt BC tại M, đường phân giác của
BCA
cắt BA tại N.
a. Hãy tính
MB
MC
. b. Chứng minh
MN AC
∥
.
Câu 6: (2,5 điểm) Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với đường thẳng AB tại E, CF
vuông góc với đường thẳng AD tại F, BH vuông góc với đường thẳng AC tại H.
a. Chứng minh:
∆∆ABH ACE∽
.
b. Chứng minh:
=..CB CF BH AC
.
c. Tia BH cắt đường thẳng CD tại Q, cắt cạnh AD tại K. Chứng minh:
=
2
.BH HK HQ
.
-- HẾT –
ĐÁP ÁN
Câu
Điểm
1
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2 điểm)
1.B 2.D 3.C 4.B 5.D 6B 7.C 8.A 9.B 10.C
0.2x10
PHẦN II. TỰ LUẬN (8 điểm)
Câu 1: (1,5 điểm) Giải phương trình
b.
( ) ( )
35
22 5
2
x
x−
−− =
( ) ( )
2.2 2 3 5 5
2
4 8 3 15 10
3
xx
xx
x
−− −=
−− + =
=
0.25
0.25
0.25
c.
( )
( )
( )
322
2 1 8 4 1 20 85x xx x− − + ++ =−
3 2 32 2
8 12 6 1 8 8 32 32 20 85
26 52
2
x xx xx x x
x
x
− + −− − − − + =−
−=−
=
0.25
0.25
0.25
2
Câu 2: (0,5 điểm) Xác định hàm số, biết đồ thị của nó là đường thẳng
d
song song với đường
thẳng
': 3 6dy x−=
và đi qua điểm
( )
1; 5A
Ta có:
:d y ax b= +
• d song song
': 3 6dy x= +
3a⇒=
• d đi qua điểm
( )
1; 5A
1, 5xy⇒= =
• Thế
3, 1, 5axy= = =
vào
:d y ax b= +
5 3.1
2
b
b
= +
=
Vậy
: 32dy x= +
0.25
0.25
3
Câu 3: (1 điểm) Xe I khởi hành từ A đến B. Sau đó 1 giờ 30 phút, trên cùng tuyến đường đó xe
II khởi hành từ B đi về A với vận tốc lớn hơn vận tốc xe I 5km/h. Sau khi xe I đi được 3 giờ 30
phút thì hai xe gặp nhau. Tính vận tốc mỗi xe biết rằng quãng đường AB dài 175 km.
Gọi x (km/h) là vận tốc của xe I (x > 0)
Ta có bảng
Xe I Xe II
0.25
0.25
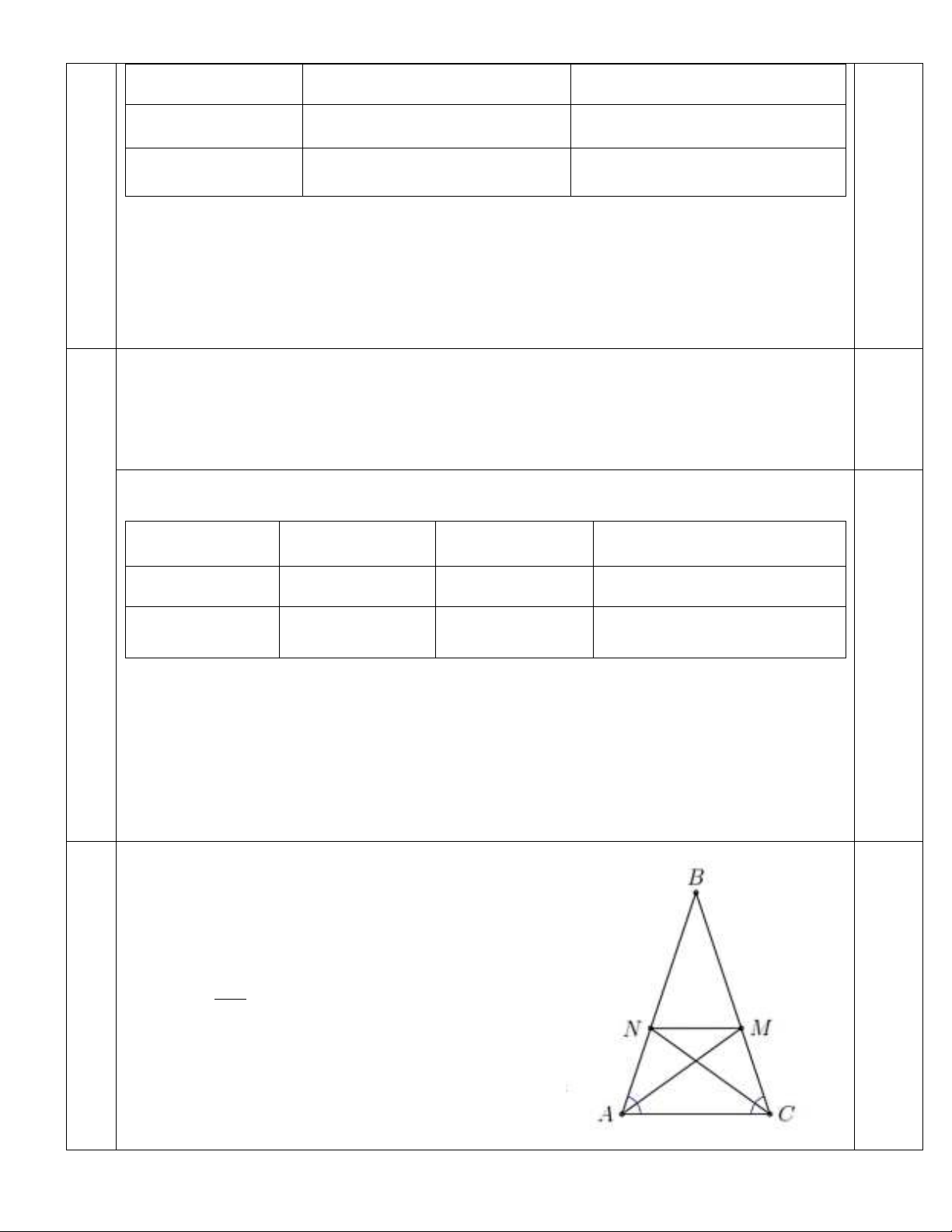
Vận tốc (km/h)
x
5x+
Thời gian (h)
3, 5
(3h30’)
2
Quãng đường (km)
3, 5x
( )
25x+
Theo đề ta có phương trình
( )
3,5 2 5 175xx+ +=
30( )xN⇔=
Vậy vận tốc của xe I là 30 km/h, vận tốc của xe II là 35 km/h.
0.25
0.25
4
Câu 4: (1,5 điểm) Bác Tuấn gửi tiết kiệm một số tiền tại ngân hàng theo thể thức kì hạn một năm
với lãi suất 4,8%/năm, tiền lãi sau mỗi năm sẽ gộp vào với tiền gốc để tính lãi cho năm tiếp theo.
Sau hai năm gửi, bác Huy rút hết tiền về và nhận được cả vốn lẫn lãi là 549 152 000 đồng. Hỏi số
tiền ban đầu bác Tuấn gửi tiết kiệm là bao nhiêu?
Gọi
x
(đồng) là số tiền ban đầu bác Tuấn gửi tiết kiệm
( )
0x>
Gốc Lãi Tổng
Năm I
x
4,8%x
4,8%xx+
Năm II
4,8%xx+
( )
4,8% 4,8%xx+
( )
4,8% 4,8% 4,8%xx xx++ +
Theo đề bài, ta có:
( )
4,8% 4,8% 4,8% 549 152 000
1,098304 549 152 000
500 000 000 (nhan)
xx xx
x
x
++ + =
=
=
Vậy số tiền ban đầu bác Tuấn gửi tiết kiệm là 500 000 000 đồng.
0.25
0.25
0.25
0.25
0.25
0.25
5
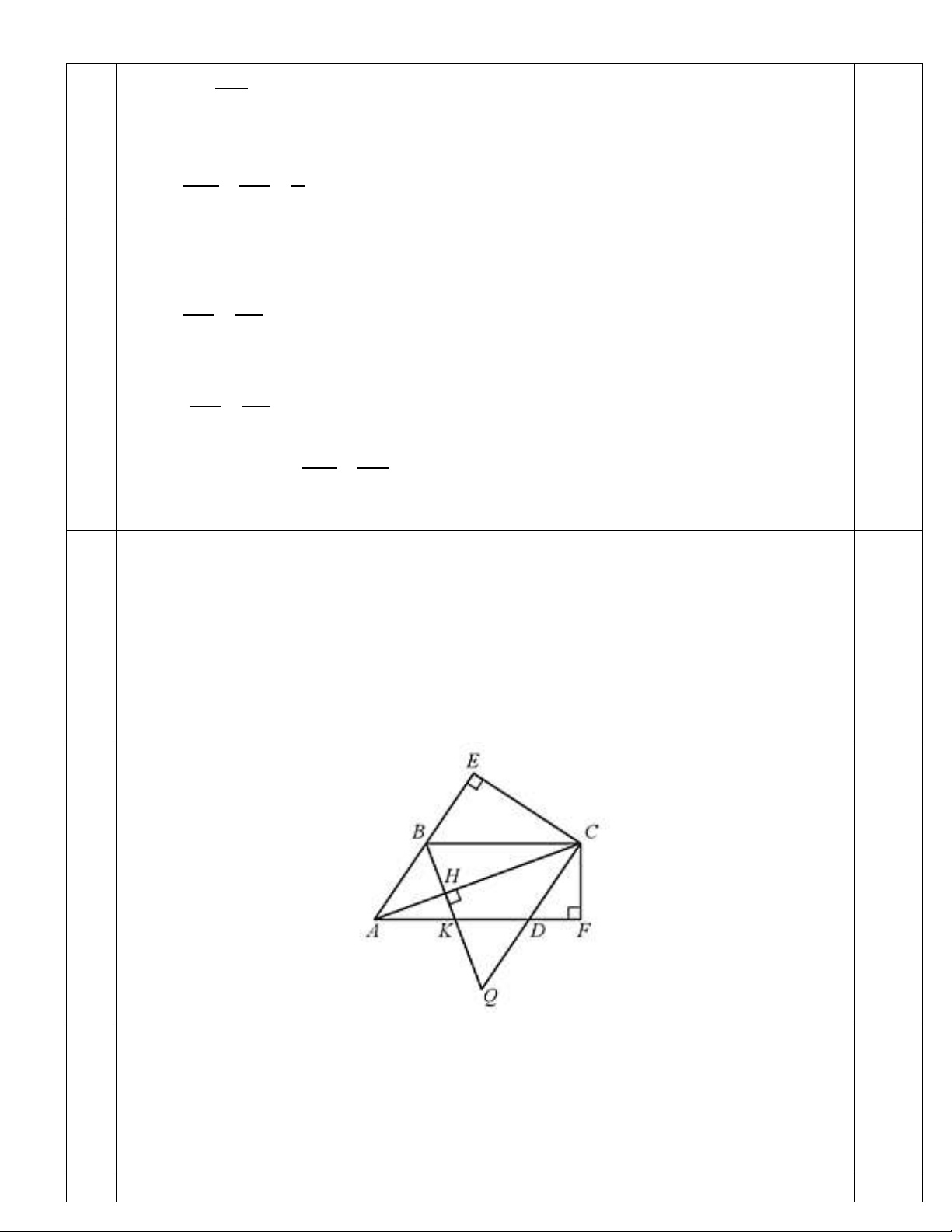
Câu 5: (1.0 điểm)
Cho tam giác ABC cân tại B,
9BA BC= =
,
4AC =
đường phân giác
BAC
cắt BC tại M, đường phân giác
BCA
cắt BA tại N. (hình vẽ minh họa bên dưới)
a. Hãy tính
MB
MC
.
b. Chứng minh
MN AC
∥
.
a. Hãy tính
MB
MC
.
Xét
ABC∆
, có AM là đường phân giác
BAC
(gt):
= = 9
4
MB AB
MC AC
(tính chất đường phân giác trong tam giác) (1)
0.25
0,25
b. Chứng minh
MN AC
∥
.
Xét
ABC∆
, có CN là đường phân giác
BCA
:
NB CB
NC CA
=
(tính chất đường phân giác trong tam giác)
Mà CB = BA (gt)
Suy ra:
NB BA
NC CA
=
(2)
Từ (1) và (2), suy ra:
MB NB
MC NC
=
Suy ra:
MN AC
∥
(định lý Thales đảo)
0.25
0.25
6
Câu 6: (2,5 điểm) Cho hình bình hành ABCD (AC>BD). Vẽ CE vuông góc với đường
thẳng AB tại E, CF vuông góc với đường thẳng AD tại F, BH vuông góc với đường thẳng
AC tại H. Chứng minh:
a.
ABH ACE∆∆∽
b.
..CB CF BH AC=
c.
2.BH HK HQ=
, biết tia BH cắt đường thẳng CD tại Q, cắt cạnh AD tại K.
a.
ABH ACE∆∆∽
• Xét
ABH∆
và
ACE∆
có:
A
: góc chung
0
90AHB AEC= =
Suy ra
ABH ACE∆∆∽
(g.g).
0.25
0.25
0.25
b.
..CB CF BH AC=