Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Hòa Phú (Đề tham khảo)

Chia sẻ: _ _ | Ngày: | Loại File: DOC | Số trang:4

Thêm vào BST

Báo xấu

6
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Các bạn hãy tham khảo và tải về “Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Hòa Phú (Đề tham khảo)” sau đây để biết được cấu trúc đề thi cũng như những nội dung chính được đề cập trong đề thi để từ đó có kế hoạch học tập và ôn thi một cách hiệu quả hơn. Chúc các bạn thi tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Hòa Phú (Đề tham khảo)

UBND HUYỆN CỦ CHI TRƯỜNG THCS HÒA PHÚ ĐỀ THAM KHẢO KIỂM TRA HKII NĂM HỌC 2022 – 2023 MÔN TOÁN LỚP 9 Thời gian làm bài : 90 phút (không kể thời gian phát đề) Bài 1: (1,5 điểm) Giải các phương trình sau: a) 5 x 2 − 8 x + 3 = 0 b) x 4 − 3x 2 − 10 = 0 Bài 2: (1,5 điểm) Cho hàm số y = x 2 có đồ thị (P) và hàm số y = −2 x + 3 có đồ thị (D). a) Vẽ đồ thị (P). b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. Bài 3: (1,5 điểm) Cho phương trình: 2 x 2 − 7 x + 6 = 0 (*) (x là ẩn số). a) Chứng minh: Phương trình (*) có hai nghiệm phân biệt. b) Gọi x1 , x2 là hai nghiệm của phương trình (*). Không giải phương trình (*), tính giá trị biểu thức: A = ( x1 + 2 x2 ) ( x2 + 2 x1 ) − x1 x2 . 2 2 Bài 4: (1 điểm) Bạn Nam mua hai cái áo sơmi và một cái nón ở cửa hàng thời trang. Nếu trả theo giá niêm yết thì Nam phải trả tổng cộng 1220 000 đồng, nhưng do cửa hàng đang có chương trình khuyến mãi nên áo sơmi được giảm 20% và nón được giảm 15% nên Nam trả số tiền ít hơn ban đầu là 228 000 đồng. Tính giá niêm yết của áo sơmi và nón ? Bài 5: (1 điểm) Bác An gửi tiền tiết kiệm vào ngân hàng kỳ hạn 1 năm với số tiền ban đầu là 100.000.000 đồng. Sau 2 năm, bác An nhận được tổng số tiền cả vốn lẫn lãi là 113.422.500 đồng. Biết rằng trong thời gian đó, lãi suất không thay đổi và bác An không rút lãi ra trong kỳ hạn trước đó. Hỏi lãi suất ngân hàng kỳ hạn 1 năm là bao nhiêu ? 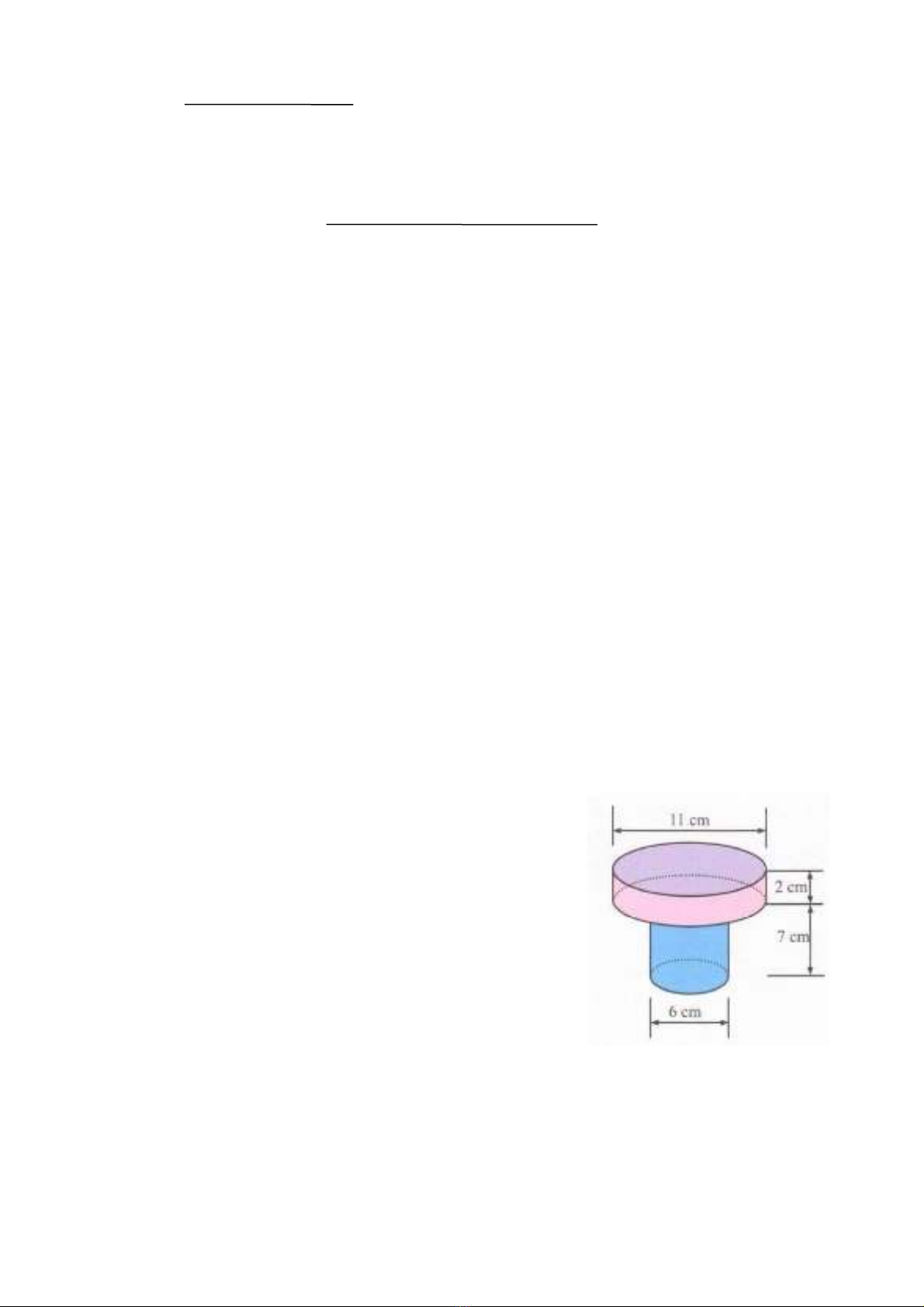Bài 6: (0,5 điểm) Một chi tiết máy có các kích thước như hình bên. Em hãy tính thể tích của chi tiết máy đó (làm tròn kết quả đến hàng đơn vị). Biết thể tích hình trụ là π r 2 h Bài 7: (3 điểm) Từ điểm M nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến MA, MB (với A, B là hai tiếp điểm) và cát tuyến MCD (điểm O nằm trong góc DMB, MC < MD). Gọi E là trung điểm của CD. a) Chứng minh: OE CD và 5 điểm A, E, O, B, M cùng thuộc một đường tròn. b) Vẽ CF song song với AM (F thuộc AE). Chứng minh: EM là phân giác của góc AEB và EFC đồng dạng với EIB. c) Gọi I là giao điểm của AB và CD. Chứng minh: FI // AC. – Hết –
ĐÁP ÁN Điểm Bài 1: (1,5 điểm) a) 5 x 2 − 8 x + 3 = 0 = 4 hoặc a + b + c = 0 0,25 x1 = 1 0,25 c 3 x2 = = 0,25 a 5 b) x 4 − 3x 2 − 10 = 0 (*) Đặt: t = x ( t 0) 2 Khi đó, (*) trở thành: t 2 − 3t − 10 = 0 (1) 0,25 = 49 0,25 ( 1) t = 5 ( nhan ) hay t = −2 ( loai ) Với t = 5 x2 = 5 x= 5 0,25 Bài 2: (1,5 điểm) a) Lập bảng giá trị đúng 0,25 Vẽ đồ thị (P) đúng 0,25 b) Phương trình hoành độ giao điểm của (P) và (D) x 2 = −2 x + 3 0,25 x2 + 2x − 3 = 0 x = 1 hay x = −3 0,25 Thay x = 1 vào (P): y = x 2 , ta được: y = 1 0,25 Thay x = −3 vào (P): y = x 2 , ta được: y = 9 0,25 Vậy: Tọa độ giao điểm của (P) và (D) là: (1; 1) , (–3; 9). Bài 3: (1,5 điểm) 2 x 2 − 7 x + 6 = 0 (*) a) ∆ = 1 > 0 Phương trình (*) có 2 nghiệm phân biệt với mọi m. 0,25 −b 7 S = x1 + x2 = = a 2 0,5 b) Theo định lý Vi – ét, ta có: c P = x1.x2 = = 3 a Ta có: A = ( x1 + 2 x2 ) ( x2 + 2 x1 ) − x1 x2 2 2 A = x1 x2 + 2 x12 + 2 x2 + 4 x1 x2 − x12 x2 2 2 0,25 A = 5 x1 x2 + 2 ( x12 + x2 ) − x12 x2 2 2 A = 5P + 2 ( S 2 − 2 P ) − P 2 A = 2S 2 + P − P 2 2 0,25 7 37 A = 2. + 3 − 32 = 2 2 0,25
Bài 4: (1 điểm) Gọi x, y (nghìn đồng) lần lượt là giá niêm yết của áo sơ mi và nón (Điều kiện: x , y > 0) Nam mua 2 áo sơ mi và 1 cái nón theo giá niêm yết trả tổng cộng 1 220 000 đồng. 2 x + y = 1220 (1) 0,25 Áo sơ mi được giảm 20%, nón được giảm 15% nên Nam trả số tiền ít hơn ban đầu là 228 000 đồng. 2.20% x + 15% y = 228 (2) 0,25 Từ (1) và (2), ta có hệ phương trình: 2 x + y = 1220 x = 450 (Nhận) 0,25 40% x + 15% y = 228 y = 320 Vậy: Giá niêm yết của áo sơ mi là 450 000 đồng, nón là 320 000 đồng. 0,25 Bài 5: (1 điểm) Gọi: x là lãi suất ngân hàng kỳ hạn 1 năm (0 < x < 1) Số tiền bác An nhận được cả vốn lẫn lãi sau 1 năm: ( 1 + x ) .100 000 000 0,25 Số tiền bác An nhận được cả vốn lẫn lãi sau 2 năm: ( 1 + x ) .100 000 000 2 Vì: sau 2 năm, bác An nhận được tổng số tiền cả vốn lẫn lãi là 113.422.500 đồng, nên: (1+ x) 2 .100 000 000 = 113 422 500 0,25 1 + x = 1,065 0,25 1 + x = −1,065 ( loai, vi :1 + x > 0 ) x = 0,065 = 6,5% Vậy: Lãi suất ngân hàng kỳ hạn 1 năm là 6,5% 0,25 Bài 6: (0,5 điểm) d1 = 11cm, h1 = 2cm d2 = 6cm, h2 = 7cm Thể tích của chi tiết máy: 2 2 11 6 247 V1 + V2 = π r h + π r h = π 2 1 1 2 2 2 .2 + π .7 = π 388 ( cm3 ) 0,5 2 2 2
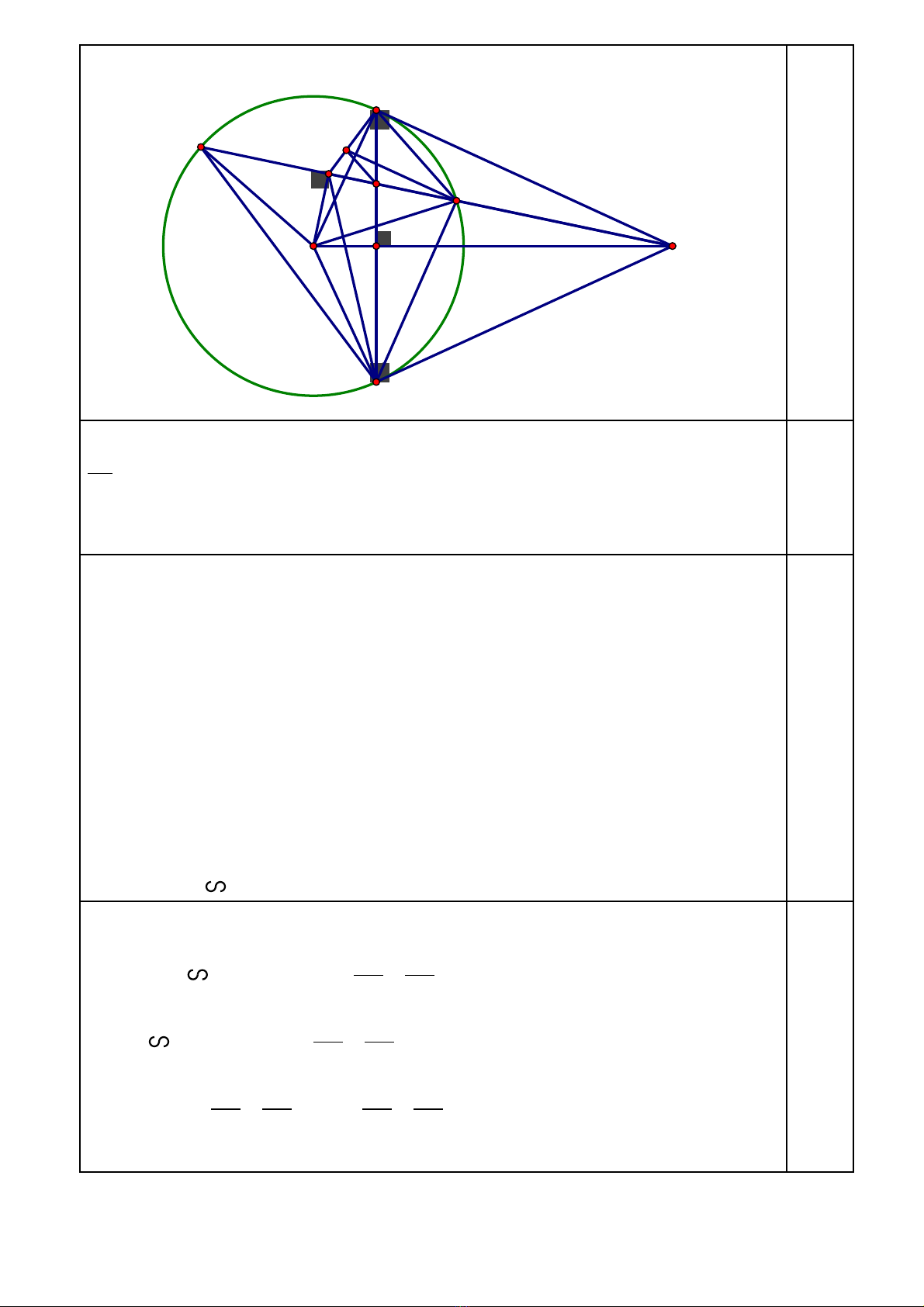
Bài 7: (3 điểm) A D F E C I O M H B a) Chứng minh: OE CD và 5 điểm A, E, O, B, M cùng thuộc một đường tròn. cm: OE CD tại E 0,5 ﾷﾷﾷ Ta có: OAM = OBM = OEM = 90o (MA, MB là tiếp tuyến (O); OE CD tại E) 0,5 A, E, O, B, M cùng thuộc đường tròn đường kính OM (cung chứa góc 90o) b) Chứng minh: EM là phân giác của góc AEB và EFC đồng dạng với EIB. Ta có: ﾷ AEM = ﾷ AOM (AEOM nội tiếp) ﾷﾷ MEB = MOB (EOBM nội tiếp) 0,25 mà: ﾷ AOM = MOB (OM là phân giác ﾷﾷ AOB ) ﾷﾷ AEM = MEB EM là phân giác của ﾷ AEB 0,25 Ta có: FCE = ﾷﾷ AME (CF // AM, đồng vị) ﾷ AME = ﾷ ABE (AEBM nội tiếp) FCE = ﾷﾷ ABE 0,25 cm: EFC EIB (g.g) 0,25 c) Chứng minh: FI // AC EA EC cm: AEC CEB (g.g) = (1) EC EB 0,25 EC EF EFC EIB (cmt) = (2) EB EI 0,25 EA EF EI EF Từ (1), (2) = = EC EI EC EA 0,5 FI // AC (Thales đảo) – Hết –