PHÒNG GIÁO D C VÀ ĐÀO T OỤ Ạ
THANH OAI
TR NG THCS THANHƯỜ
THÙY
Đ THI CH N H C SINH GI I HUY NỀ Ọ Ọ Ỏ Ệ
NĂM H C 2015-2016Ọ
MÔN: TOÁN L P 9Ớ
Th i gian làm bài 150 phút không k th i gian giaoờ ể ờ
đề
Bài 1: (6 đi m) ểCho bi u th c: .ể ứ
a) Rút g n bi u th c P.ọ ể ứ
b) Tìm x đ P > 0.ể
c) Tính giá tr c a P v i x =ị ủ ớ
Bài 2: (4 đi m) ể
a) Gi i ph ng trình:ả ươ
b) Tìm các nghi m nguyên c a ph ng trình: 2xệ ủ ươ 2 + 4x = 19 - 3y2
Bài 3: (2 đi m) ể
a) Cho x,y,z là ba s d ng th a mãn: ố ươ ỏ . Tìm giá tr l n nh t c a Q = xyzị ớ ấ ủ
b) Cho tam giác ABC có đ dài ba c nh là a,b,c và có chu vi là 2. Ch ng ộ ạ ứ
minh r ng: aằ2 + b2 +c2 + 2abc < 2.
Bài 4: (2 đi m) ểCho ΔABC vuông A . Bi t AB = 3cm , AC = 4 cm. T Bở ế ừ
v tia Bx vuông góc v i BC T i B , Bx c t CA tai đi m E. trên đo n th ngẽ ớ ạ ắ ể ạ ẳ
BE l y F b t k , h BH vuông góc v i FC t i H.ấ ấ ỳ ạ ớ ạ
a) Tính AE.
b) Ch ng minh ΔAHC Δứ FEC.
Bài 5: (6 đi m)ể
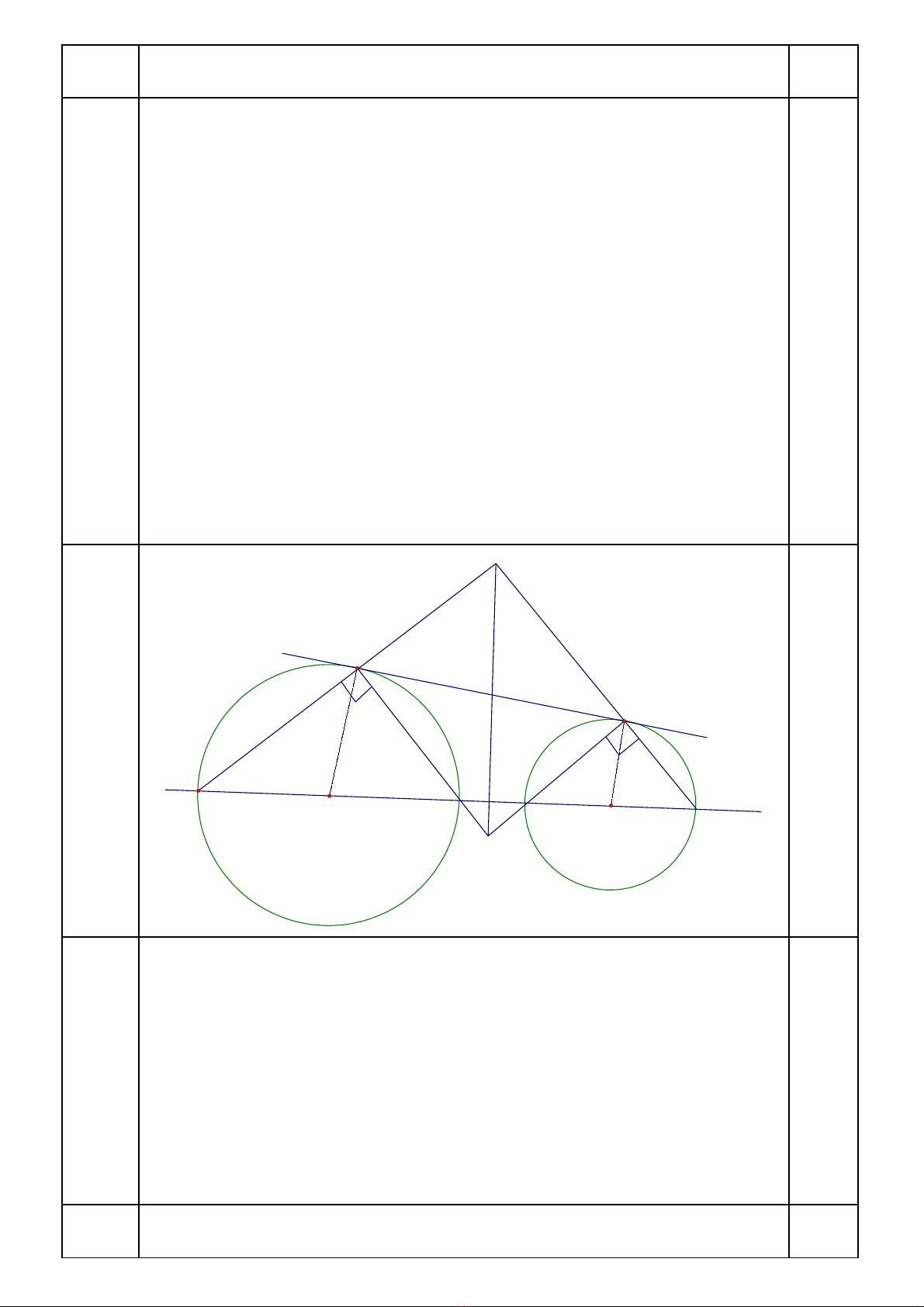
Cho hai đng tròn ( O ) và ( Oườ / ) ngoài nhau. Đng n i tâm OOở ườ ố / c tắ
đng tròn ( O ) và ( Oườ / ) t i các đi m A, B, C, D theo th t trên đngạ ể ứ ự ườ
th ng. K ti p tuy n chung ngoài EF, E ( O ) và F ( Oẳ ẻ ế ế / ). G i M là giao đi mọ ể
c a AE và DF; N là giao đi m c a EB và FC. Ch ng minh r ng:ủ ể ủ ứ ằ
a) T giác MENF là hình ch nh t.ứ ữ ậ
b) MN AD.
c) ME.MA = MF.MD.
---------- H t ----------ế
Ng i ra đ T tr ng duy t Duy t BGHườ ề ổ ưở ệ ệ
H NG D N CH M , BI U ĐI M ƯỚ Ẫ Ấ Ể Ể
Đ TOÁN 9 NĂM H C 2015-2016Ề Ọ
BàiĐáp ánĐiể
m
1ĐKXĐ: 0,5 đ
a)
0,5 đ
0,5 đ
0,5 đ
b) P > 0
x > 4
K t lu n: x > 4 và x ≠ 9 thì P > 0 ế ậ
0,5đ
0,5đ
0,5đ
0,5đ
c)
x =
=> x3 = 4 + 3..x
x3 + 3x 4 = 0
x3 x2 + x2 x + 4x 4 = 0
x2(x – 1) + x(x – 1) + 4(x – 1) = 0
(x – 1)( x2 + x + 4) = 0
Vì x2 + x + 4 > 0 nên x – 1 = 0 => x = 1
V y P = ậ
0,5đ
0,5đ
0,5đ
0,5đ
Bài 2
a) Đk : 4 ≤ x ≤ 6
= 6 − x
= 6 – x
+ x – 6 = 0
. (2 + ) = 0
= 0 x = 4
(2 + ) = 0 ( vô lý)
Th l iử ạ : – x 2 = 2
K t lu nế ậ : V y ph ng trình có nghi mậ ươ ệ : x = 4
Tìm nghi m nguyên c a ph ng trìnhệ ủ ươ
0,5 đ
0,5 đ
0,5 đ
0,5 đ
b)
2x2 + 4x = 19 – 3y2
2x2 + 4x + 2 = 21 – 3y2
2(x2 + 2x + 1) = 3(7 – y2)
2(x+1)2 = 3(7 – y2)
7 – y2 > 0
7 – y2 2
y2 là s l , mà 7 – yố ẻ 2 > 0
y ch có th là ỉ ể
2(x+1)2 = 3.6 = 18
(x+1)2 = 32
x = −4 ; x = 2
(x,y) = (-4, 1) ; (-4, -1) ; (2, -1) ; (2,1)
0,5 đ
0,5 đ
0,5 đ
0,5 đ
Bài 3
a)
≥ 2
T ng tươ ự : ≥ 2
≥ 2
Nhân v v i v ta đcế ớ ế ượ :
≥ 2.2.2 = 8.
1 ≥ 8xyz
≥ xyz hay xyz ≤
Max Q = khi x = y = z =
0,5đ
0,5đ
0,5đ)
(0,5đ)
b) Ta có:
0 < a < b + c => 2a < a + b + c => a < 1
0 < b < a + c => 2b < a + b + c => b < 1
0 < c < b + a => 2c < a + b + c => c < 1
=> (a – 1) (b – 1) (c – 1) < 0
abc – (ac +ab + bc) + (a+b+c) < 1
2abc – 2(ac +ab + bc) + (a+b+c)2 < 2 (vì a + b + c = 2)
2abc + a2 + b2 + c2 < 2 (đccm)
0,5đ)
(0,5đ)
(0,5đ)
(0,5đ)
Bài 4: v hình đúng ẽ
AB2 = CA. AE
=> AE =
CH. CF = BC2 (△ HBC △ BFC)
CA. CE= BC2 (△ ABC △ BEC)
=> CH. CF = CA. CE
=>
Góc C chung
=> △ AHC △ FEC (c.g.c)
0,5đ
0,5đ
0,5đ
0,5đ
Bài 5
H
D
E
M
F
O
I
N
O
/
B
C
A
0,5đ
a) Ta có
Góc AEB = GócCFD = 90
0 (góc n i ti p ch n n a đng tròn)ộ ế ắ ữ ườ
Vì EF là ti p tuy n chung c a hai đng tròn (O) và (Oế ế ủ ườ /), nên:
OE EF và OF EF => OE // O/F
Góc EOB= Góc FO’D (góc đồng vị) => góc EAO = góc FCO’
Do đó MA // FN, mà EB MA => EB FN
Hay góc ENF = 90
0.
T giác MENF có , nên MENF là hình ch nh tứ ữ ậ
0,5 đ
0,5 đ
0,5 đ
b) G i I là giao đi m c a MN và EF; H là giao đi m c a MN và ADọ ể ủ ể ủ
Vì MENF là hình ch nh t, nên góc IFN = góc INFữ ậ 0,5 đ
M t khác, trong đng tròn (Oặ ườ /):gocsIFN= góc FND = ½ sđ cung FC
=>góc FDC = góc FDC
Suy ra đng d ng (g – g)ồ ạ
=> góc NHC= góc DFC = 900 hay MN AD
0,5 đ
0,5 đ
0,5 đ
c)
Do MENF là hình ch nh t, nên góc MFE = FENữ ậ
Trong đng tròn (O) có: góc FEN = góc EAB =1/2 sđ cung EBườ
=>gócMEF = EAB
Suy ra đng d ng (g – g)ồ ạ
=>, hay ME.MA = MF.MD
0,5 đ
0,5 đ
0,5 đ
0,5 đ
L u ý:ư N u ếh c sinhọ gi i theo cách khác, ản uế đúng và phù h p v i ki nợ ớ ế
th c trong ch ng trình ứ ươ đã h c ọthì hai Giám kh o ảch m thi th ng nh t vi c phânấ ố ấ ệ
b đi m c a cách gi i đó, sao cho không làm thay đi t ng đi m c a ố ể ủ ả ổ ổ ể ủ bài (ho c ý)ặ
đã nêu trong h ng d n này.ướ ẫ /.
NG I SOÁT T TR NG DUY T BGHƯỜ Ổ ƯỜ Ệ