Đề thi học sinh giỏi môn Toán lớp 12 cấp tỉnh năm 2020-2021 - Sở GD&ĐT Bình Thuận

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:6

Thêm vào BST

Báo xấu

13
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Với mong muốn giúp các em có thêm tài liệu ôn tập thật tốt trong kì thi chọn HSG sắp tới. TaiLieu.VN xin gửi đến các em Đề thi học sinh giỏi môn Toán lớp 12 cấp tỉnh năm 2020-2021 - Sở GD&ĐT Bình Thuận. Vận dụng kiến thức và kỹ năng của bản thân để thử sức mình với đề thi nhé! Chúc các em đạt kết quả cao trong kì thi học sinh giỏi sắp tới.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học sinh giỏi môn Toán lớp 12 cấp tỉnh năm 2020-2021 - Sở GD&ĐT Bình Thuận

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH BÌNH THUẬN MÔN TOÁN – LỚP 12 NĂM HỌC 2020 - 2021 TOANMATH.com Thời gian làm bài: 180 phút (không kể thời gian phát đề) Đề thi gồm 01 trang + 05 bài toán tự luận Bài 1. (6,0 điểm) a. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   x  11 x 2  9 trên đoạn  0; 4 . b. Cho hàm số đa thức y  f ( x) có đồ thị như sau: y 1 1 O 2 x Tìm số điểm cực trị của hàm số y  f  x 2  2 x  2  . ab Bài 2. (5,0 điểm) Xét dãy số  un  thỏa u1  a  b, un 1  u1  , n  * ; trong đó a , b là hai số thực un dương. a. Chứng minh  un  là dãy số giảm khi a  b; b. Tính lim un .  x  xy  1 Bài 3. (3,0 điểm) Tìm tất cả các giá trị thực của tham số m để hệ phương trình  có ba 3 x  y  m  0 2 nghiệm phân biệt. Bài 4. (2,0 điểm) Cho hai số nguyên dương k và n sao cho k  n. Xét tất cả các tập hợp con gồm k phần tử của tập hợp 1, 2,..., n . Trong mỗi tập hợp con ta chọn ra phần tử nhỏ nhất. Chứng minh tổng tất cả các phần tử được chọn bằng Cnk11 . Bài 5. (4,0 điểm) Cho đường tròn  O  có đường kính AB cố định, M là điểm di động trên  O  sao cho M khác với các điểm A, B và OM không vuông góc với AB. Các tiếp tuyến của  O  tại A và M cắt nhau tại C. Gọi  I  là đường tròn đi qua M và tiếp xúc với đường thẳng AC tại C. Đường thẳng OC cắt lại  I  tại điểm thứ hai là E. a. Chứng minh E là trung điểm của OC ; b. Gọi CD là đường kính của  I  . Chứng minh đường thẳng qua D và vuông góc với BC luôn đi qua một điểm cố định khi M di động trên  O  . ____________________ HẾT ____________________
LỜI GIẢI CHI TIẾT Câu 1. a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   x  11 x 2  9 trên đoạn  0;4 . b) Cho hàm số đa thức y  f  x  có đồ thị như sau: Tìm số điểm cực trị của hàm số y  f  x 2  2 x  2  . Lời giải a) Hàm số đã cho liên tục trên đoạn  0;4 .  x  1  TM  2 x 2  11x  9 Ta có y  , y  0   . x2  9  x  9  KTM   2 Ta có y  0   33, y 1  10 10, y  4   35 . Vậy min y  35, max y  10 10 . 0;4 0;4 b) Đặt g  x   f  x 2  2 x  2  . Ta có g   x   2  x  1 f   x 2  2 x  2  . Gọi x  x1 , x  x2 , x  x3 (với x1  x2  x3 ) là các điểm cực trị của hàm số f  x  . Từ đồ thị, ta có x1   1;0  , x2   0;1 , x3  1;2  . x  1 x 1   2 x 1  0  x 2  2 x  2  x1  x  2 x  2  x1  0 1 Ta có g   x   0    2  2 .  f   x  2 x  2   0 x  2 x  2  x2  0  2  2 x  2 x  2  x2    x 2  2 x  2  x3  x 2  2 x  2  x3  0  3  Xét phương trình (1), ta có   1   2  x1   x1  1  0 nên phương trình (1) vô nghiệm. Xét phương trình (2), ta có   x2  1  0 nên phương trình (2) vô nghiệm. Xét phương trình (3), ta có   x3  1  0 nên phương trình (3) có hai nghiệm phân biệt khác 1. Như vậy phương trình g   x   0 có ba nghiệm đơn nên hàm số g  x  có ba điểm cực trị. ab Câu 2. Xét dãy số  un  thỏa u1  a  b, un 1  u1  , n  * ; trong đó a, b là hai số thực dương. un a) Chứng minh  un  là dãy số giảm khi a  b . b) Tính lim un . Lời giải
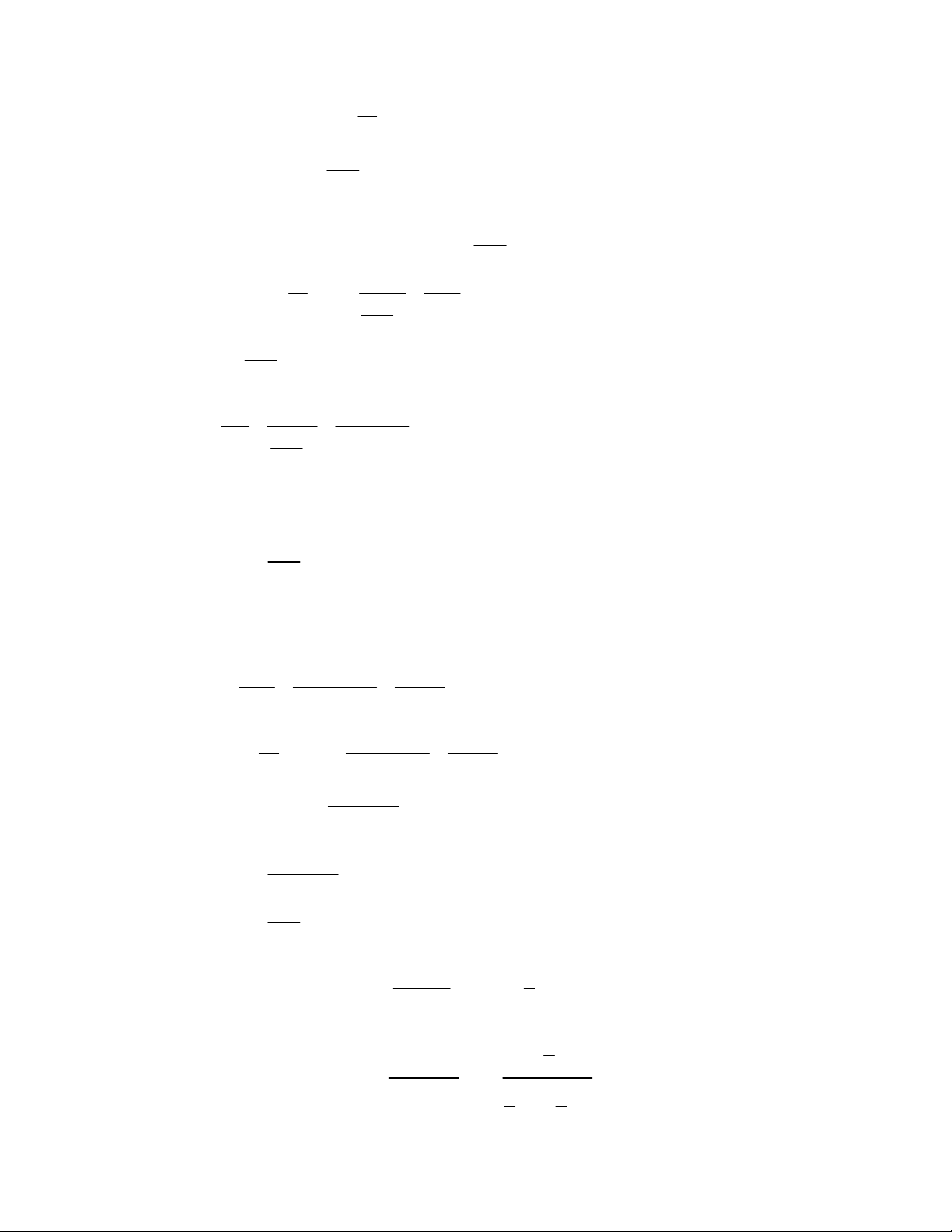
u1  2a  a) Khi a  b , ta có  a2 .  n1 1 u , n     * u u  n n 1 Ta chứng minh: un  a, n  * 1 bằng phương pháp quy nạp. n  Ta có: u1  2a  1 đúng với n  1 . k 1  Giả sử 1 đúng với n  k , tức là: uk  a ;  k  1 . k a2 a2 k2 Ta có: uk 1  u1   2a   a  1 đúng với n  k  1 . uk k  1 k  1 a k n 1 Vậy un  a, n  * 1 , ta có un  0, n  * n n2 a un 1 n  1 n 2  2n Ta có   2  1, n  * . Vậy  un  là dãy số giảm . un n 1 n  2 n  1 a n b) Không mất tính tổng quát, giả sử a  b. * Trường hợp 1: a  b n 1 Khi đó un  a, n  * . n * Trường hợp 2: a  b Khi đó: ab a 2  ab  b 2 a 3  b3 u2  a  b    2 ; ab ab a  b2 ab ab  a 2  b 2  a 4  b 4 u3  a  b   ab  3 3; u2 a3  b3 a b a n 1  b n 1 Qui nạp ta được un  , n  * . a n  bn  a n 1  b n 1  n khi a  b Do đó un   a  b n , n   * . n 1 a khi a  b  n * Khi a  b, ta có lim un  lim  n  1 a  lim 1  1  a  a .   n  n n 1 b 1   a n 1  bn 1 a * Khi a  b, ta có lim un  lim  lim a. a n  bn 1 b  n 1     a   a  
Vậy lim un  a.   x  xy  1 Câu 3. Tìm tất cả các giá trị của tham số m để hệ phương trình   2 có ba nghiệm phân      3 x y m 0 biệt. Lời giải  x  xy  1 1 Xét hệ phương trình:   2 . 3 x  y  m  0 2  Điều kiện: xy  0 . Vì x  0 không phải là nghiệm của phương trình nên x  0 . Ta có : (1)  xy  1 x . 1 x  0  x  1     . 1  xy  1 x2  y   2  x   x 1 Thay vào phương trình (2) ta có: 3 x 2   2  x  m (3). x Để hệ phương trình có ba nghiệm phân biệt thì phương trình (3) có ba nghiệm phân biệt thuộc ;1 \ 0 . 1 Xét hàm số f  x  3 x 2   2  x , x  ;1 \ 0 . x 1 6 x 3  x 2 1 Ta có: f   x   6 x  2  1  . x x2 1 f   x   0  6 x 3  x 2 1  0  x  . 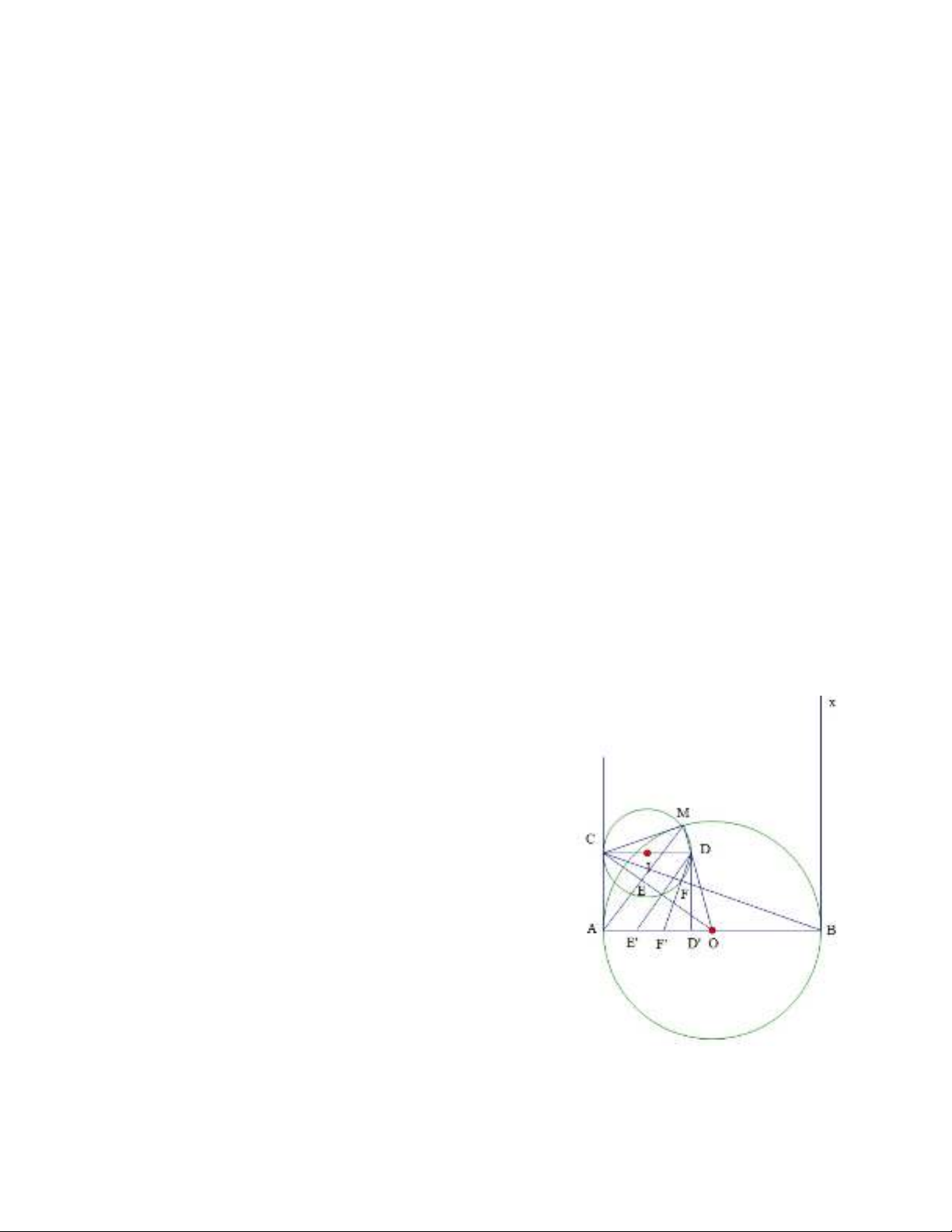2 Bảng biến thiên: Số nghiệm của phương trình (3) là số giao điêm của đồ thị hàm số y  f  x  và đường thẳng y  m. Dựa vào bảng biến thiên ta thấy phương trình (3) có ba nghiệm phân biệt thuộc ;1 \ 0 5  khi m   ;3 .  4    5  Vậy m   ;3 thì hệ phương trình  x  xy  1  4   2 có ba nghiệm phân biệt.  3 x  y  m  0 
Câu 4. Cho hai số nguyên dương k và n sao cho k  n. Xét tất cả các tập hợp con gồm k phần tử của tập hợp 1, 2,..., n . Trong mỗi tập hợp con ta chọn ra phần tử nhỏ nhất. Chứng minh tổng tất cả các phần tử được chọn bằng Cnk11 . Lời giải Theo đề bài ta có: TH1: Tập có phần tử nhỏ nhất là số 1 có Cnk11 tập. TH2: Tập có phần tử nhỏ nhất là số 2 có Cnk22 tập. … TH k: Tập có phần tử nhỏ nhất là số 2 có Cnkkk tập. Suy ra tổng các phần tử được chọn là Cnk11  Cnk22  ...  Cnkkk . Dễ dàng ta chứng minh được Cnk11  Cnk22  ...  Cnkkk  Cnk11 (đpcm). Câu 5. Cho đường tròn  O  có đường kính AB cố định, M là điểm di động trên  O  sao cho M khác với các điểm A, B và OM không vuông góc với AB. Các tiếp tuyến của  O  tại A và M cắt nhau tại C. Gọi  I  là đường tròn đi qua và tiếp xúc với đường thẳng AC tại C. Đường thẳng OC cắt lại  I  tại điểm thứ hai là E. a) Chứng minh E là trung điểm của OC . b) Gọi CD là đường kính của  I  . Chứng minh đường thẳng qua D và vuông góc với BC luôn đi qua một điểm cố định M di động trên  O  . Lời giải  a) Có MCO   EC  EM ACO  CME Mà CMO vuông tại M  M là trung điểm OC . b) Vẽ DF  BC  F  ( I ) DE  AB  E ', DD '  AB F ' là trung điểm của AO  F ' cố định Ta có CD / / E ' O (  CA) E là trung điểm của CO  CDOE ' là hình bình hành Mà CDD ' A là hình chữ nhật  D ' A  CD  E ' O  F là trung điểm D ' E ' Gọi Bx là tiếp tuyến tại B của (O ) . Có: ( BC , Bx, BM , BA)  1 . Mà BC  DF , Bx  DC , BM  DE , BA  DD ' ( BM  AM , AM  OC , OC  DE )  ( DC , DF , DE , DD ')  1 .
Mà DC / / AB  DF qua trung điểm D ' E ' .  D, E ', F '  DF qua F ' cố định. ____________________ HẾT ____________________