.
2222
d
dcba
c
dcba
b
dcba
a
dcba
PHÒNG GD & ĐT YÊN LẠC
TRƯỜNG THCS LIÊN CHÂU
ĐỀ KHẢO SÁT HSG LẦN 1, NĂM HỌC 2020-2021
Môn: Toán 7
Thời gian: 120 phút
Câu 1: (2 điểm) a) Cho dãy tỉ số bằng nhau :
Tính giá trị của biểu thức
.
cb
ad
ba
dc
ad
cb
dc
ba
M
b) Số 200! Có tận cùng bao nhiêu chữ số 0
Câu 2: (2 điểm): Tìm x, y, z biết:
a) 2009 –
2009x
= x b)
2008
2008 2
2 1 0
5
x y x y z
Câu 3: ( 2 điểm)
a) Tìm x biết:
2 7 3
5 5 5
x
b)Tìm giá trị nhỏ nhất của biểu thức: Q =
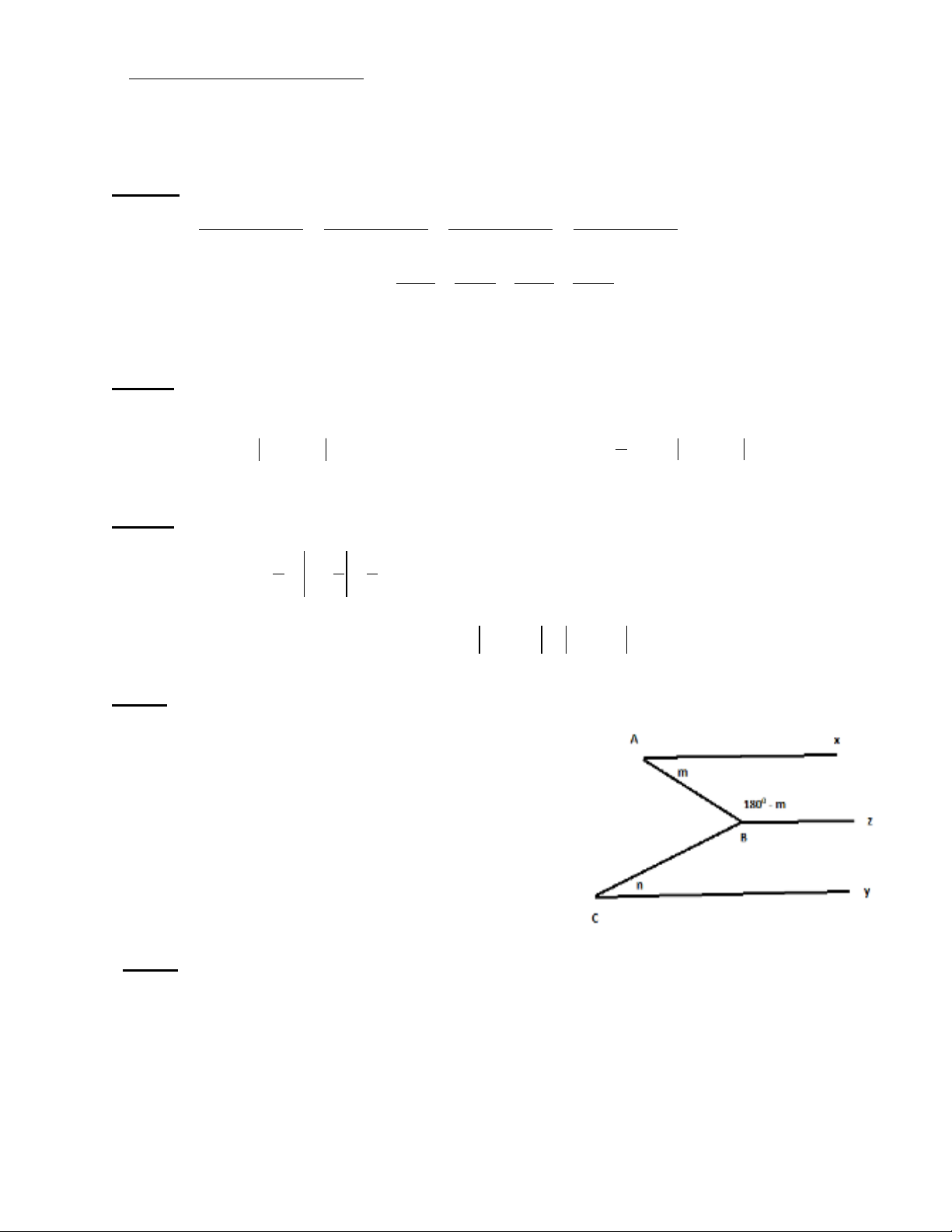
Câu 4 : (2 điểm): Cho hình vẽ . Biết :
00
00
00
;;
;
180
A m C n
ABC m n
ABZ m
Chứng minh rằng: a) Ax // Bz
b) Ax // Cy.
Câu 5(2điểm): a) Tìm x, y
N biết:
2
2
36 8 2010yx
b) Cho 100 số hữu tỉ trong đó tích của bất kì 3 số nào cũng là một số âm.
Chứng minh rằng : Tích của 100 số đó là một số dương và tất cả 100 số đó là số âm.
................... Hết .....................
2 2 2 3xx

HDC ĐỀ KS HSG TOÁN 7 LẦN 1
NĂM HỌC 2020-2021
CÂU
Đáp án
Điểm
Câu
1,a)
(1đ)
a.(1đ) Từ giả thiết suy ra
d
dcba
c
dcba
b
dcba
a
dcba
d
dcba
c
dcba
b
dcba
a
dcba
1
2
1
2
1
2
1
2
* Nếu a + b + c + d = 0 thì a + b = - (c + d); b + c = - (d + a);
c + d = - ( a + b); d + a = - ( b + c)
Khi đó M = (- 1) + (- 1) +(- 1) +(- 1) = - 4
* Nếu a + b + c + d
0 thì
dcba
1111
nên a = b = c = d
Khi đó M = 1 + 1 + 1 +1 = 4
Vậy
396
5
25
1
:
1980
1
B
A
0,25
0,25
0,25
0,25
Câu
1,b)
(1đ)
Ta có: 200! = 1.2.3.4.5.....198.199.200.
Do 10 = 2.5
Để có 1 chữ số 0 tận cùng ta cần một cặp thừa số 2 và 5.
Do 2<5 nên số thừa số 2 có trong 200! nhiều hơn số thừa số 5 có trong 200! Khi phân
tích ra thừa số nguyên tố.
Vậy số chữ số 0 tận cùng của 200! Đúng bằng số thừa số 5 có trong tích 200! Khi
phân tích ra thừa số nguyên tố
Bắt đầu từ thừa số 1, Cứ 5 số lại có một bội của 5, cứ 25 = 52 số lại có một bội của
25, cứ 125 = 53 số lại có một bội của 125....
Như vậy khi phân tích 200! Ra thừa số nguyên tô có số thừa số 5 là:
234
200 200 200 200
5 5 5 5
= 40 + 8 + 1 + 0
= 49
Vậy 200! Có 49 chữ số 0 tận cùng.
0,5
0,5
Câu 2:
a)
a) 2009 –
2009x
= x
- Nếu x
2009
2009 – x + 2009 = x
2.2009 = 2x
x = 2009
- Nếu x < 2009
2009 – 2009 + x = x
0 = 0
Vậy với
x < 2009 đều thoả mãn.
- Kết luận : với x
2009 thì
2009 2009xx
0,25
0,25
0,25
0,25

Câu
2: b)
a)
2008
2008 2
2 1 0
5
x y x y z
(*)
Với mọi x,y,z ta luôn có:
2008
2008 2
2 1 0; 0; 0
5
x y x y z
Nên (*) sảy ra khi:
2008
2008
1
2 1 0 2 1 0 2
2 2 2
00
5 5 5
09
0
10
x
xx
y y y
x y z
x y z z
Vậy:
1
2
x
;
2
5
y
;
9
10
z
0,25
0,5
0,25
Câu
3: a)
73
55
2 7 3
5 5 5 72
55
3 7 3 42
5 5 5 5
72 4
11
55 5
49
3 7 3 22
55
5 5 5 9
72 5
55
x
x
x
xx
x
xx
xx
x
x
x
0,25
0,5
0,25
Câu 3
b)
Q =
=
Dấu “=” xẩy ra khi
Vậy min Q = 5 khi
3
12
x
0,5
0,25
0,25
2 2 2 3xx
2 2 3 2xx
2 2 3 2 5xx
1
2 2 0 3
1
3
3 2 0 2
2
x
xx
xx
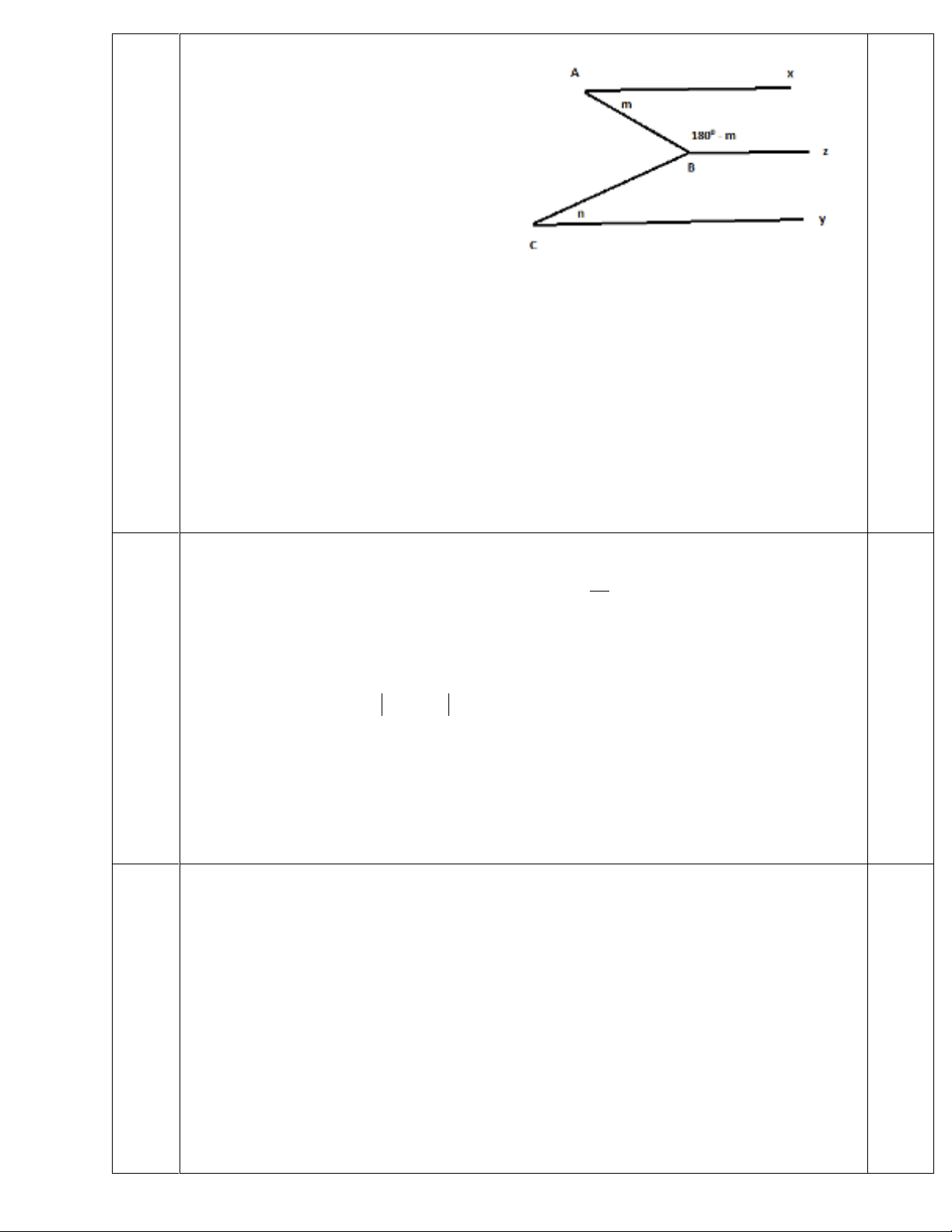
Câu 4
a)
00
0
180
180
xAB ABZ m m
Mà
xAB
và
ABz
là hai góc
trong cùng phía.
Vậy: Ax // Bz(1)
b)
0 0 0 0 0
00
360 180
180
CBz m n m
n
0 0 0 0
180 180CBz C n n
Mà
CBz
và
C
là hai góc trong cùng phía
Suy ra Bz // Cy (2)
Từ (1) và (2) suy ra Ax // Cy.
0,25
0,5
0,25
0,25
0,5
0,25
Câu 5
a)
Ta có:
2
2
36 8 2010yx
2
28 2010 36yx
.
Vì
20y
2236
8 2010 36 ( 2010) 8
xx
Vì
2
0 ( 2010)x
và
xN
,
2
2010x
là số chính phương nên
2
( 2010) 4x
hoặc
2
( 2010) 1x
hoặc
2
( 2010) 0x
.
+ Với
22012
( 2010) 4 2010 2 2008
x
xx
x
22
42( )
y
yy loai
+ Với
22
( 2010) 1 36 8 28xy
(loại)
+ Với
2
( 2010) 0 2010xx
và
26
36 6 ( )
y
yy loai
Vậy
( , ) (2012; 2); (2008;2); (2010;6).xy
0,25
0,25
0,25
0,25
Câu 5
b)
b) *V ì tích của 3 số bất kì là một số âm nên trong 100 số đó luôn tồn tại ít nhất một số
âm. Ta chọn ra 1 số âm này, 99 số còn lại ta chia thành 33 nhóm, mỗi nhóm có 3 số. Do
tích của 3 số bất kì là một số âm nên tích của 99 số này đúng bằng tích của 33 số âm và
cũng bằng một số âm.
Suy ra tích của 100 số đã cho là một số dương.
*Gọi 100 số đã cho được sắp xếp theo thứ tự tăng dần là:
a1; a2; a3; a4; ……….,; a98; a99; a100
Xét tích : a98. a99. a100 là số âm. Nên a98. a99. a100 < 0
Suy ra a98 < 0
Cứ như vậy ta chỉ ra được a1; a2; a3; a4; ……………..; a97 là số âm.
Xét tích a1. a2. A98 < 0 . do a1; a2 âm nên a98 âm.
Tương tụ ta chỉ ra được a99 âm.
Vậy tất cả 100 số đã cho đều là số âm.
0,25
0,25
0,25
0,25













![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



