Đề thi học sinh giỏi môn Toán lớp 8 cấp trường năm 2019-2020 có đáp án - Trường THCS Phú Hải

Chia sẻ: Thiên Thần | Ngày: | Loại File: PDF | Số trang:6

Thêm vào BST

Báo xấu

21
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Việc ôn thi sẽ trở nên dễ dàng hơn khi các em có trong tay Đề thi học sinh giỏi môn Toán lớp 8 cấp trường năm 2019-2020 có đáp án - Trường THCS Phú Hải được chia sẻ trên đây. Tham gia giải đề thi để rút ra kinh nghiệm học tập tốt nhất cho bản thân cũng như củng cố thêm kiến thức để tự tin bước vào kì thi chính thức các em nhé! Chúc các em ôn tập đạt kết quả cao!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học sinh giỏi môn Toán lớp 8 cấp trường năm 2019-2020 có đáp án - Trường THCS Phú Hải

PHÒNG GD&ĐT PHÚ VANG TRƯỜNG THCS PHÚ HẢI ĐỀ THI HSG TOÁN 8 CẤP TRƯỜNG Năm học: 2019 - 2020 Thời gian: 120 phút( không kể thời gian giao đề) ----------------------------------------------- Bài 1(3 điểm). Cho a – b = 5 và a.b = 2. Tính : a) A = a3 – b3 b) B = 3(a4 + b4) + 2(a5 – b5) Bài 2(4 điểm). a) Tìm GTLN của các biểu thức: A = – (x + 2)4 + 3(x – 1)2 + x(x + 22) – 5. b) Phân tích đa thức sau thành nhân tử: A = (x2 – 3x + 1)(x2 + 2x + 1) – 6x2 Bài 3(4 điểm). 4 6 11 7 a) Giải phương trình :    2 x  12 x  3 2 x  32 x  9 2 x  92 x  20 24 b) Tính tổng: S = 31 – 21 + 32 – 22 + 33 – 23 + … + 32019 – 22019. Bài 4 (5 điểm). 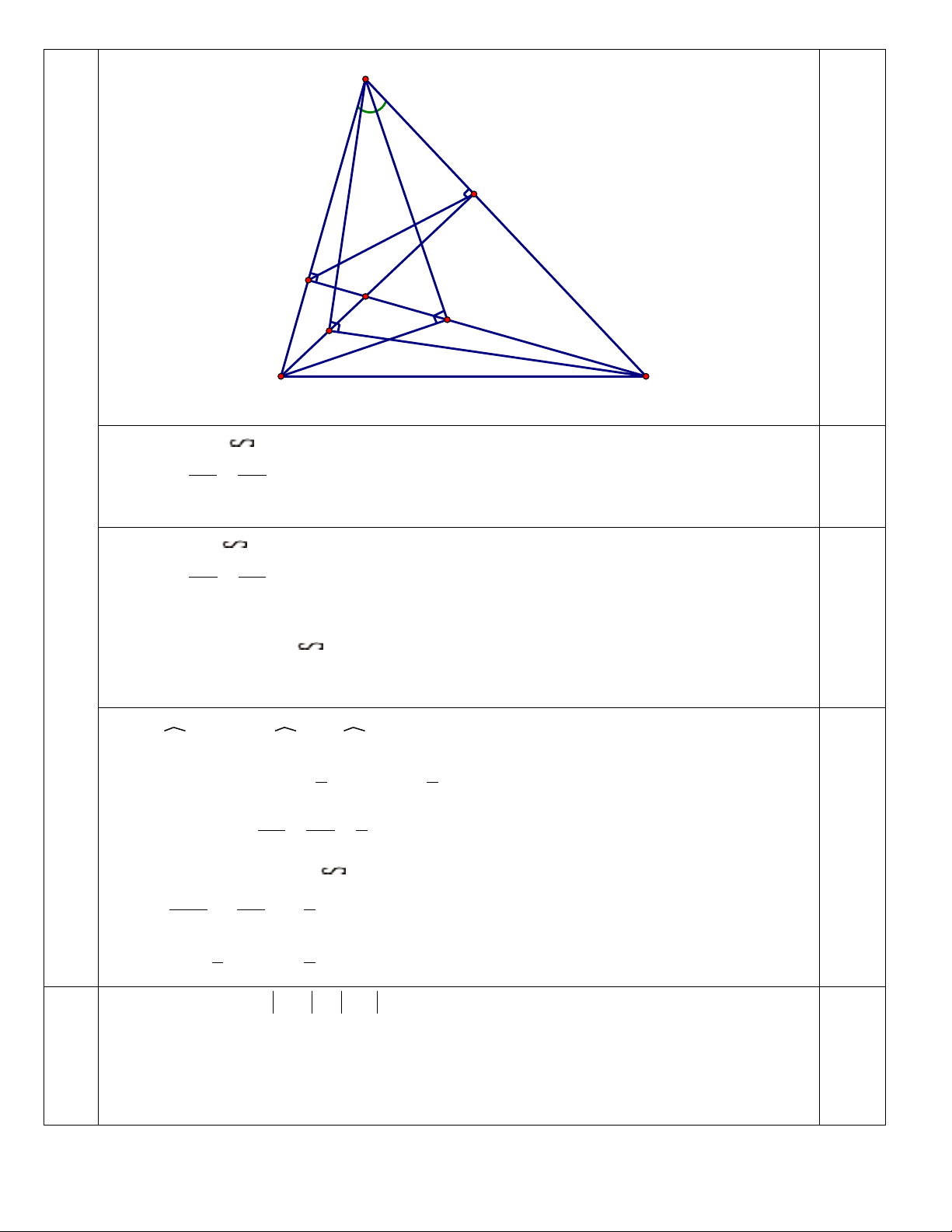Cho tam giác ABC nhọn. Trên các đường cao BE, CF, lần lượt lấy các điểm I, K sao cho AIC = 900 và AKB = 900. a) Chứng minh AF. AB = AE. AC b) Chứng minh AI = AK c) Cho A = 600, SABC = 120cm2. Tính diện tích tam giác AEF. Bài 5 (2 điểm). Tìm x để biểu thức A = x  3  2 x  1 + 1 có giá trị không âm. Bài 6 (2 điểm). Cho tam giác đều ABC. M, N là các điểm lần lượt chuyển động trên hai cạnh BC và AC sao cho BM = CN. Xác định vị trí của M, N để độ dài đoạn thẳng MN nhỏ nhất . -------------------------------------Hết----------------------------------- 1
ĐÁP ÁN Bài Nội dung Điểm 1 a) A = (a – b)(a + ab + b ) = 5[(a – b)2 + 3ab] = 5(25 + 3.2) = 155 2 2 1đ (3đ) b)  a4 + b4 = (a2 + b2)2 – 2a2b2 = [(a – b)2 + 2ab]2 – 2a2b2 0,5đ = (25 + 2.2)2 – 2.22 = 833  a – b = (a + b )(a – b ) + a2b3 – a3b2 5 5 2 2 3 3 = [(a – b)2 + 2ab] . (a – b)(a2 + ab + b2) + a2b2(b – a) = [(a – b)2 + 2ab] . (a – b) [(a – b)2 + 3ab] + a2b2(b – a) = (25 + 4) . 5. (25 + 6) – 4.5 =4475 1đ Vậy B = 3. 833 + 2 . 4475 = 11449 0,5đ 2 a) B = – (x + 2)4 + 4x2 + 16x – 2 (4đ) = – (x + 2)4 + 4(x + 2)2 – 18 = – 14 –  x  22  2 2  14 1đ  x  2  2 Đẳng thức xảy ra khi và chỉ khi (x + 2) 2 – 2 = 0   0,5đ  x  2  2 Vậy GTLN của B bằng – 14 khi x = – 2 + 2 hoặc x = – 2 – 2 0,5đ b) A = (x2 – 3x + 1)(x2 + 2x + 1) – 6x2 2  x  3x  1 x  2 x  1  2 2 x   .  6   x x   1  1    x 2  x   3  x   2   6  x  x   0,5đ 1 Đặt t = x  , khi đó: x  1  1   x   3  x   2   6 = (t – 3)(t + 2) – 6 = t – t – 12 2  x  x  = (t + 3)(t – 4) =  x   3  x   4  1 1 1đ  x  x  Vậy: A = x2  x   3  x   4  1 1  x  x     =  x x   3   x x   4  1 1   x    x  = (x2 + 3x + 1)(x2 – 4x + 1) 0,5đ 2
3 (4đ) 4 6 11 7 a)    (1) 2 x  12 x  3 2 x  32 x  9 2 x  92 x  20 24 1 3 9 ĐK: x  , x   , x   , x  10 2 2 2 (1)   1 1   1 1   1 1  7       0,5đ  2 x  1 2 x  3   2 x  3 2 x  9   2 x  9 2 x  20  24 1 1 7    2 x  1 2 x  20 24  242 x  20  242 x  1  72 x  12 x  20  2 x 2  19 x  46  0   x  2 2 x  23  0 1đ x  2 thoa    x   23 thoa   2 Vậy tập nghiệm của phương trình là: S = 2 ;   23 0,5đ  2 b) S = 31 – 21 + 32 – 22 + 33 – 23 + … + 32019 – 22019. 0,5đ = (31 + 32 + 33 + … + 32019) – (21 + 22 + 23 + …+ 22019) Đặt A = 31 + 32 + 33 + … + 32019, B = 21 + 22 + 23 + …+ 22019  A = 31 + 32 + 33 + … + 32018 + 32019 3A = 32 + 33 + 34 + … + 32019 + 32020  3A – A = 32020 - 31 3 2020  3 0,5đ A = 2  B = 21 + 22 + 23 + …+ 22018 + 22019 2B = 22 + 23 + 24 + … + 22019 + 22020  2B – B = 22020 - 21 0,5đ B = 2 2020 –2 3 2020  3 3 2020  2 2021  1 Vậy S = 2  2 2020 2   2 0,5đ 3
A 4 (5đ) E F 0,25đ K I B C a)  AEB  AFC 0,25đ AE AB   AF AC  AF . AB  AE . AC (1) 0,5đ b)  AIE  ACI  AI  AE 0,5đ AC AI  AI  AE . AC (2) 2 0,5đ Tương tự :  AKF  ABK  AK  AF . AB (3) 2 0,5đ Từ (1), (2), (3) suy ra: AI = AK. 0,5đ c) A = 600  ABE = ACF = 300 nên: 0,5đ 1 1  AE = AB, AF = AC 2 2  AE AF 1   0,5đ AB AC 2 Suy ra :  AAEF  ABC 2 S AEF  AE  1 0,5đ    S ABC  AB  4 1 1  SAEF = .SABC = . 120 = 30 (cm2) 4 4 0,5đ 5 Ta cần tìm x để : x  3  2 x  1 + 1  0 (*) 0,25đ (2đ)  x+3  0  x  -3  x+3
Ta có bảng xét dấu: x -3 1 - 0 + 0,25đ x+3 + x-1 - - 0 + Xét các trường hợp sau: 1. khi x < - 3: (*)   x  3  2x  2  1  0 0,5đ  x  4 (loại) 2. Khi  3  x  1 : (*)  x  3  2x  2  1  0 2 x 3 2 Kết hợp với điều kiện đang xét ta được   x  1 0,5đ 3 3. 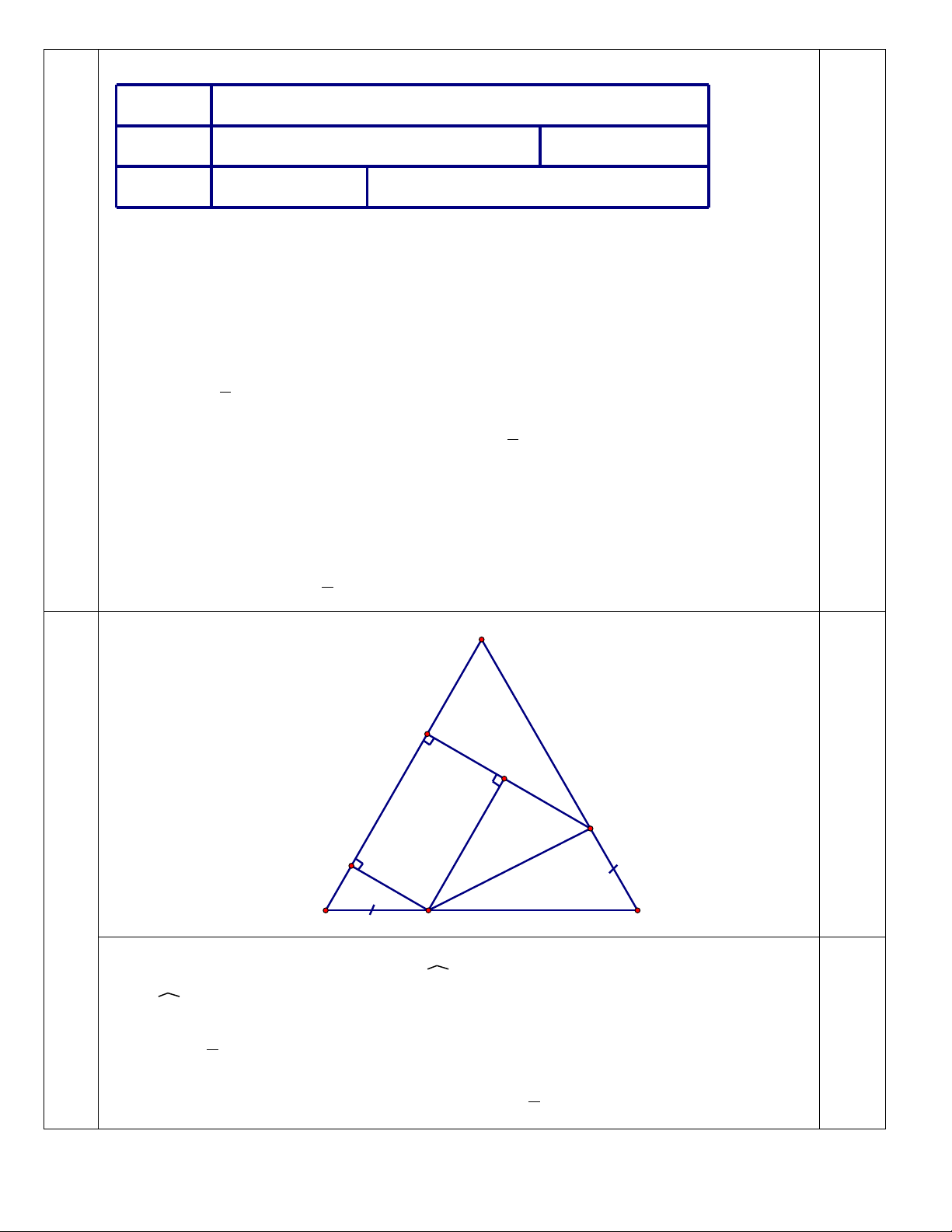Khi x > 1: (*)  x  3  2x  2  1  0 x6 Kết hợp với điều kiện đang xét ta được 1  x  6 2 Tóm lại x cần tìm là :   x  6 0,5đ 3 6 A (2đ) E H 0,25đ N D B M C Gọi D và E là chân đường vuông góc kẻ từ M và N xuống AB Ta có tam giác ANE vuông ở E có A = 600  ANE = 300 1 0,5đ  AE = AN 2 1 Tương tự đối với tam giác MDB ta có DB = BM 2 5
Do đó : AE + DB = 1 1 1 1 1 AN + BM = (AN + BM) = (AN + NC ) = AC 0,25đ 2 2 2 2 2 Kẻ MH  EN, khi đó tứ giác DEHM là hình chữ nhật. Ta có MN ≥ MH 0,5đ 1 1 Mà: MH = DE = AB – ( AE + BD ) = AB – AC = AB 2 2 1 Suy ra: MN ≥ AB 2 1 Vậy đọan MN có độ dài nhỏ nhất bằng AB . Khi M, N lần lượt là trung 0,5đ 2 điểm của BC và AC. ( Mọi cách giải đúng đều cho điểm tối đa) Giáo viên ra đề Huỳnh Văn Quý 6