Đề thi học sinh giỏi môn Toán lớp 9 cấp huyện năm 2020-2021 có đáp án - Phòng GD&ĐT Yên Thế

Chia sẻ: Agatha25 Agatha25 | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

19
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Nhằm đánh giá lại thực lực học tập của các em học sinh trước khi tham dự kì thi HSG sắp tới. Mời các em học sinh và giáo viên cùng tham khảo Đề thi học sinh giỏi môn Toán lớp 9 cấp huyện năm 2020-2021 có đáp án - Phòng GD&ĐT Yên Thế để tích lũy kinh nghiệm làm bài trước kì thi. Chúc các em thi tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học sinh giỏi môn Toán lớp 9 cấp huyện năm 2020-2021 có đáp án - Phòng GD&ĐT Yên Thế

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHỌN HỌC SINH GIỎI YÊN THẾ VĂN HOÁ CẤP HUYỆN NĂM HỌC 2020 - 2021 ĐỀ THI CHÍNH THỨC MÔN THI: TOÁN; LỚP: 9 PHỔ THÔNG Đề thi có 02 trang Ngày thi: 30 /10/2020 Mã đề: T102 Thời gian làm bài 120 phút, không kể thời gian giao đề I.PHẦN TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm) Hãy lựa chọn các phương án em cho là đúng: Câu 1. Cho A  1! 2! 3! ....  n! ( n  N * ). Tìm n để A là số chính phương? A. n=4 . B. n=3. C. n=2 . D. n  5 . Câu 2. Trên mặt phẳng tọa độ Oxy, cho hai điểm A(3; 3) và B(3;3). Đường trung trực của đoạn thẳng AB có phương trình là: x x A. y   . B. y  . C. y   x. D. y  x. 2 2 x  ;  d 2  : y  1 x  1 ; 2 2 Câu 3. Trên mặt phẳng tọa độ Oxy cho ba đường thẳng  d1  : y  3 3 3 2  d3  :  2m  3 x  3my  0 . Tìm m để ba đường thẳng đã cho đồng quy? 1 1 3 2 A. . B. . C. . D. . 4 4 2 3 Câu 4. Cho tam giác ABC cân tại A có A  300 , AB=6 (cm). Độ dài cạnh BC bằng: A. 6  3 3 B. 6 C. 6 2  3 D. 72  36 3 Câu 5: Điều kiện của x thỏa mãn 2 x  1  x  1 là: A. Không tồn tại x B. x ≥ -2 C. x ≥ 1 D. x ≤ -1 Câu 6: Dư của phép chia đa thức P(x) = x99 + x55 + x11 + x + 5 cho x2 - 1 là: A. 5 B. 2x - 5 C. 4x + 5 D. 5x + 5 Câu 7. Trên mặt phẳng tọa độ Oxy, hệ số góc tạo bởi đường thẳng có phương trình y  6  x bằng: A. 70o. B. 30o. C. 45o. D. 135o. Câu 8: Cho đường tròn (O; 5cm), dây AB = 8 cm. Khoảng cách từ tâm O đến dây AB bằng: A. 3 B. 6 C. 4 D. 5 Câu 9. Cho tam giác ABC vuông tại A. Kẻ AH  BC , HD  AB, HE  AC  H  BC, D  AB, E  AC  . Đẳng thức nào sau đây đúng ? A. AD. AB  AE. AC. B. BD.BA  CE.CA. C. AD.DB  AE.EC  2 AH . 2 D. BD.BA  AH . 2 Câu 10. Cho x  3 10  6 3  3 1  . Giá trị của biểu thức  x 3  4 x  2021 2020 bằng: 62 5  5 A. 20212020. B. 20212020. C. 2020. D. 2021. Câu 11: Tổng các hệ số của đa thức trong khai triển (x2 - 2xy + y2)7 bằng: A. 1 B.0 C. 4 D. -2
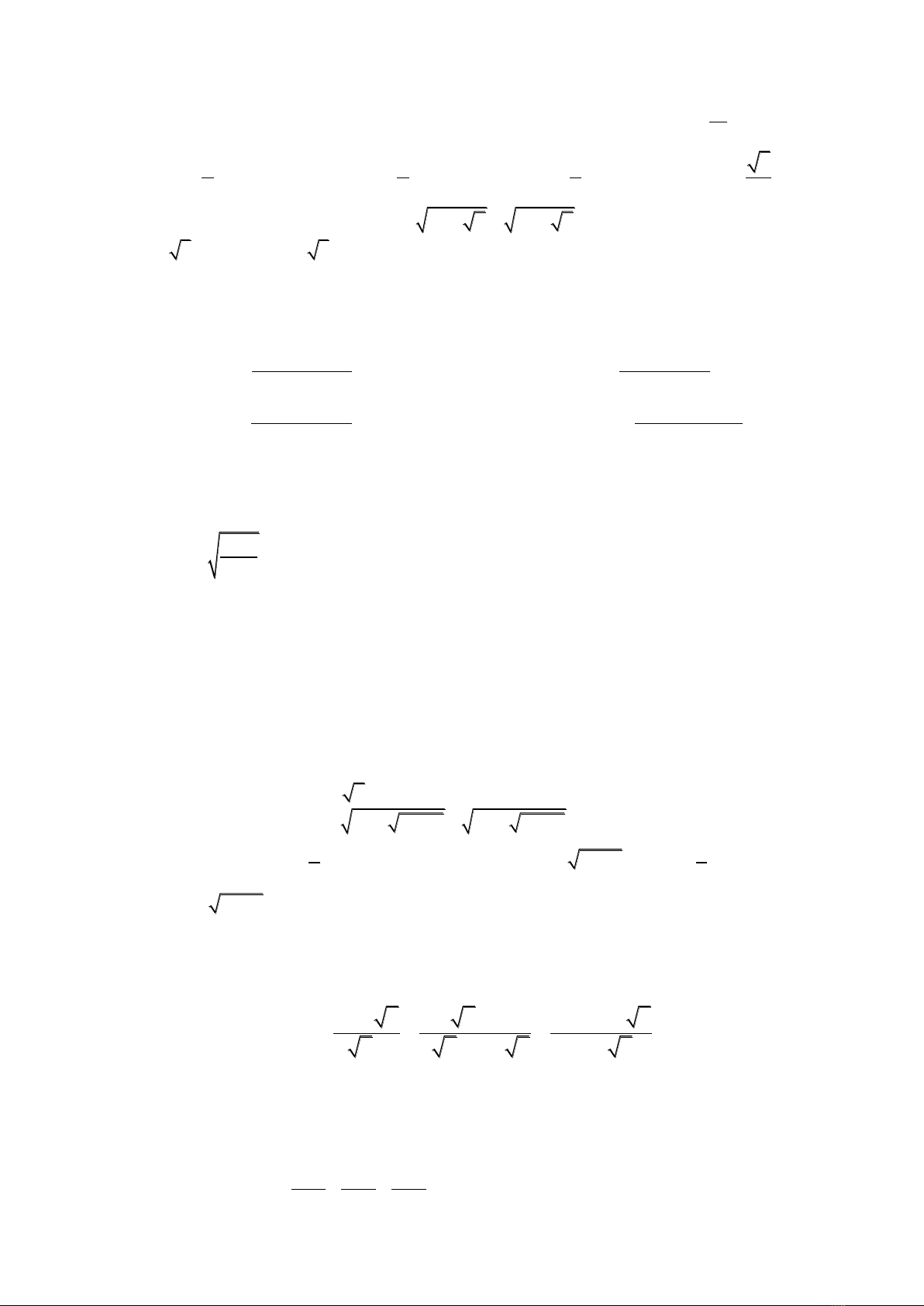
Câu 12. Cho tam giác nhọn ABC có BAC  300 , kẻ hai đường cao BD, CE S'  D  AC; E  AB  . Gọi S ; S ' lần lượt là diện tích ABC, ADE . Tỉ số bằng: S 3 1 1 3 A. . B. . C. . D. . 4 4 2 2 Câu 13: Giá trị của biểu thức M  3  2 2  3  2 2 bằng: A. 2 3 B. - 2 3 C. -2 D. 2 Câu 14. Cho tam giác nhọn ABC có ABC  ACB , kẻ đường cao AH, trung tuyến AM  M , H  BC  . Đẳng thức nào sau đây đúng ? cot C - cot B cot B - cot C A. tan HAM  . B. tan HAM  . 2 2 tan C - tan B cos C - cos B C. tan HAM  . D. tan HAM  . 2 2 Câu 15: Số dư của A = 3n + 3 + 2n + 3 + 3n + 1 + 2n + 2 khi chia cho 6 là: A. 0 B. 2 C. 1 D. 3 4 x Câu 16: có nghĩa khi: x 3 A. 3  x  4 B. 3  x  4 C. 3  x  4 D. 3  x  4 Câu 17: Tổng các ước tự nhiên của số 100 là: A. 217 B. 216 C. 218 D. 219 Câu 18. Trong góc phần tư thứ nhất của hệ trục tọa độ Oxy cho điểm M , biết rằng M thuộc đường thẳng y  2  x và cách đều hai trục tọa độ Ox và Oy. Hoành độ của điểm M bằng: A. 1. B. 1. C. 2. D. 2. Câu 19. Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm M  2021; 2021 đến đường thẳng y  x  2 bằng: A. 2. B. 2. C. 4. D. 1. Câu 20. Cho biểu thức P  2 x  8x  4  2 x  8x  4 , khẳng định nào dưới đây đúng ? 1 1 A. P  2 với mọi x  . B. P  2 2 x  1 với mọi  x  1. 2 2 C. P  2 2 x  1 với mọi x  1. D. P  2 với mọi x  R . II. PHẦN TỰ LUẬN ( 14 điểm): Câu 1. (4,0 điểm) x2 x x 1 1  2x  2 x 1. Cho biểu thức P    . x x 1 x x  x  x x2  x Rút gọn P và tìm tất cả các giá trị của x sao cho giá trị của P là một số nguyên. 2. Cho các số dương a, b, c thỏa mãn ab  bc  ca  1 . ab bc c a Chứng minh rằng:   0 1  c2 1  a 2 1  b2 Câu 2. (4,0 điểm)
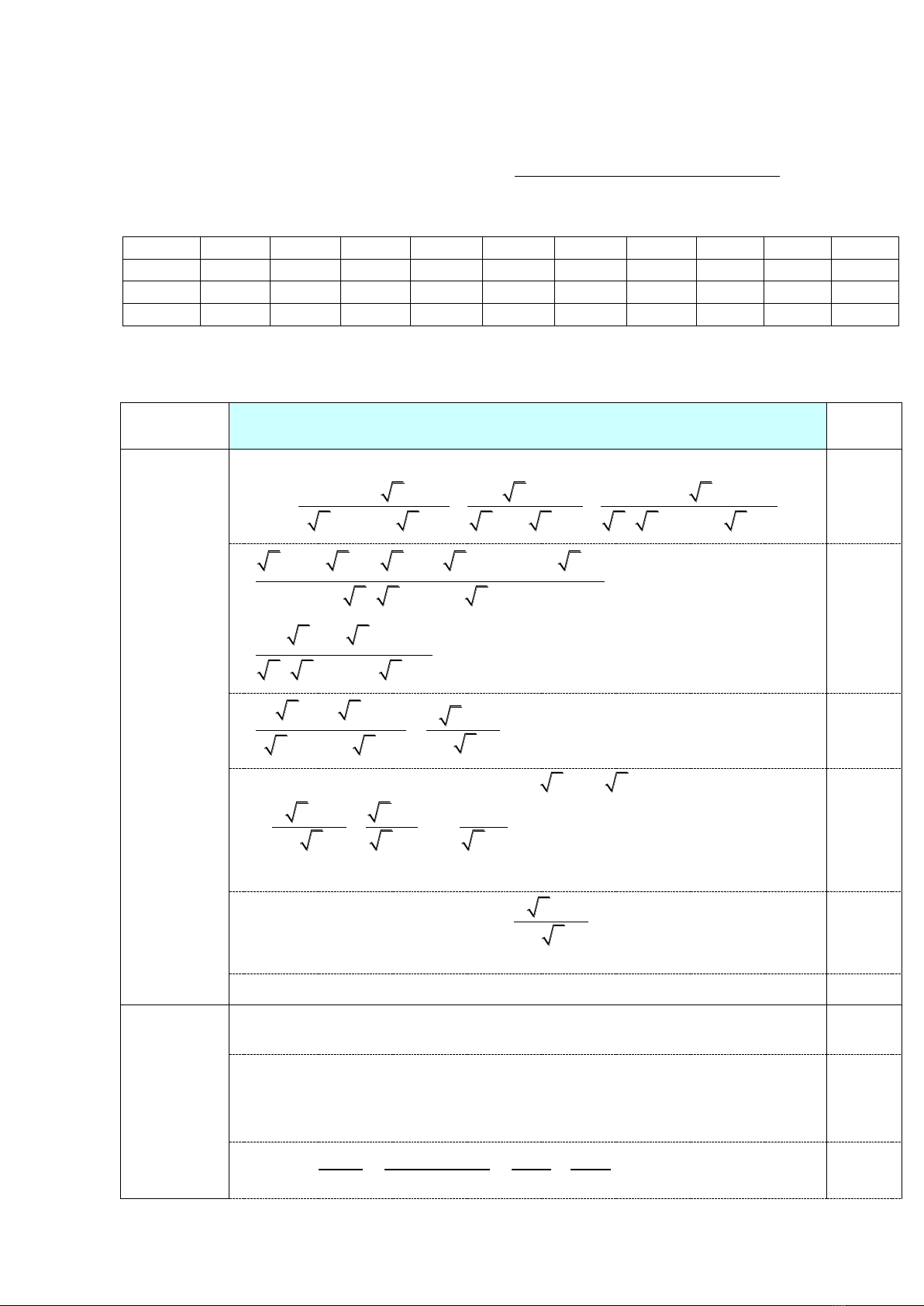
1. Tìm tất cả các số nguyên x, y thỏa mãn x2  y 2  xy  x  y  1 . 2. Giải phương trình 2 2 x 1  x  3  5x  11  0 . Câu 3. (2,0 điểm Hai vị trí A và B cách nhau 615 m và cùng nằm về một phía bờ sông. Khoảng cách từ A, B đến bờ sông lần lượt là 118 m và 487 m (tham khảo hình vẽ bên). Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi được bằng bao nhiêu mét (làm tròn đến đơn vị mét). Câu 4. (3,0 điểm): Cho hình vuông ABCD có cạnh bằng a, biết hai đường chéo cắt nhau tại O. Lấy điểm I thuộc cạnh AB, điểm M thuộc cạnh BC sao cho IOM  900 (I và M không trùng với các đỉnh của hình vuông). Gọi N là giao điểm của AM và CD, K là giao điểm của OM và BN. 1) Chứng minh ΔBIO = ΔCMO và BKM  BCO . 1 1 1 2) Chứng minh 2 = 2 + . CD AM AN 2 Câu 5. (1,0 điểm) Cho a, b, c là các số thực dương thỏa mãn 2ab  6bc  2ac  7abc . Chứng minh 4ab 9ac 4bc rằng: C     17 . a  2b a  4c b  c ---------------Hết---------------- Cán bộ coi thi không giải thích gì thêm. Họ và tên thí sinh: .................................................................Số báo danh:......................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM KỲ THI CHỌN HỌC SINH GIỎI YÊN THẾ VĂN HOÁ CẤP HUYỆN NĂM HỌC 2020-2021 ĐỀ THI CHÍNH THỨC MÔN THI: TOÁN; LỚP: 9 PHỔ THÔNG Mã đề: T102 Ngày thi: 30 /10/2020 Thời gian làm bài 120 phút, không kể thời gian giao đề I.PHẦN TRẮC NGHIỆM KHÁCH QUAN (6,0 điểm) Mỗi câu đúng cho 0,3 điểm Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B D B C C C C A A A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án B A D A A C A A B B II. PHẦN TỰ LUẬN ( 14 điểm): Hướng dẫn giải (4.0 Câu 1 điểm) Điều kiện x  0, x  1 , ta x2 x x 1 2x  2 x 1 0,50 có: P      x 1 x  x  1    x x x  x 1  x 1 x  x  1  x x  2 x x  1 x  1  2 x  2 x  1  xx  1 x  x  1 0,50 x  x  x  2  x  x  1 x  x  1 1   x 1 x  2  x  2 .  x 1 x  x  1 x  x  1 (2.0 điểm) 0,50 Ta có với điều kiện x  0, x  1  x  x  1  x  1  1  P  0 x 2 x 2 1 P   1 2 0,50 x  x 1 x 1 x 1 Do đó: 0
bc bc 1 1    ; 1 a 2 (a  b)(a  c) a  c a  b ca ca 1 1    . 1 b 2 (b  a)(b  c) b  a b  c Vậy a b b c c a 1 1 1 1 1 1 0,50          0. 1 c 1 a 1 b 2 2 2 cb ca ac ab ba bc (4.0 Câu 2 điểm) Ta có x 2  y 2  xy  x  y  1   x  y    x  1   y  1  4 0,75 2 2 2 Ta có bảng giá trị tương ứng (học sinh có thể xét từng trường hợp) 1,0 x y x 1 y 1 2 0 0 2 -2 0 0 (2.0 điểm) 0 2 0 0 -2 0 0 0 2 0 0 -2 Vậy các số  x; y  cần tìm là 1;1 ,  1;1 , 1; 1 0,25 1 Điều kiện x  0,25 2 2 2 x  1  x  3  5x  11  0  2 2 x  1  x  3  5 x  11 2 (2.0 điểm)  9 x  1  4 2 x2  5x  3  5x  11  2 x 2  5x  3  3  x 0,5 x  3 x  3 x  1 0,75  2   2  2 x  5 x  3  9  6 x  x  x  11x  12  0  x  12 2 Đối chiếu điều kiện ta được x  1 là nghiệm duy nhất của phương trình. 0,5 KL:……. (Chú ý: Thiếu KL trừ 0,25 đ, thiếu điều kiện trừ 0,25 đ) (4 Câu 3 điểm) 0,25 (2.0 điểm) Gọi C, D lần lượt là hình chiếu của A, B lên bờ sông. Đặt
CE  x  0  x  492  Ta có CD  6152   487  118  492. 2 Quãng đường di chuyển của người đó bằng AE  EB 0,25  x 2  1182   492  x   4872 2 0,25 a 2  b2  c 2  d 2   a  c   b  d  2 2 Ta có với mọi a, b, c, d thì (1). Thật vậy 1  a 2  b2  c 2  d 2  2 a 2  b2  c 2  d 2    a  c    b  d  2 2  a 2  b2  c 2  d 2   ac  bd (2) Nếu ac  bd  0 thì (2) luôn đúng. Nếu ac  bd  0 bình phương hai vế ta 0,25 được (2) trở thành  ad  bc   0. Dấu đẳng thức sảy ra khi ad  bc. 0,25 2 Áp dụng (1) thì 0,25 AE  EB   x  492  x    487  118  608089  779,8m 2 2 Dấu đẳng thức xảy ra khi 487 x  118  492  x   x  96m 0,25 Vậy quãng đường nhỏ nhất là 780 m 0,25 (3điể Câu 4 m) A I B O M K E D C N 1 (1.5 điểm) Xét BIO và CMO có: IBO  MCO ( 450 ) ( tính chất đường chéo hình vuông) BO = CO ( tính chất đường chéo hình vuông) 0,50 BOI  COM ( cùng phụ với BOM )  BIO = CMO (g.c.g) Ta có BIO = CMO (cmt)  CM = BI ( cặp cạnh tương ứng)  BM = AI 0,50 BM AM IA AM Vì CN // AB nên    . Từ đó suy ra IM // BN CM MN IB MN Ta có OI = OM ( vì BIO = CMO )  IOM cân tại O 0,50
 IMO  MIO  450 Vì IM // BN  BKM  IMO  450  BKM  BCO Qua A kẻ tia Ax vuông góc AN cắt CD tại E. 0,25 Chứng minh ADE  ABM ( g.c.g )  AE  AM Ta có ANE vuông tại A có AD  NE nên AD.NE AN . AE 0,5 S AEN    AD.NE  AN .AE  ( AD.NE )2  ( AN .AE )2 2 2 2(1.5điểm) Áp dụng định lí Pitago vào ANE ta2 có AN 2 + AE2 = NE2 AN  AE 2 1 1 1 1  AD .( AN  AE )  AN . AE  2 2 2 2 2 2 2  2  2  2  0,25 AN . AE AD AE AN AD 2 1 1 1 Mà AE  AM và CD = AD  2  2  0,5 CD AM AN 2 1 Câu 5 điểm Từ gt : 2ab  6bc  2ac  7abc và a,b,c > 0 2 6 2 Chia cả hai vế cho abc > 0     7 c a b 1 1 1  x, y , z  0 0.25 đặt x  , y  , z    a b c 2 z  6 x  2 y  7 4ab 9ac 4bc 4 9 4 Khi đó C       a  2b a  4c b  c 2 x  y 4 x  z y  z 1.0 điểm 4 9 4 C   2x  y   4x  z   y  z  (2 x  y  4 x  z  y  z ) 2x  y 4x  z yz 0.25 2 2  2   3   2 2    x  2y     4x  z     y  z   17  17  x  2y   4x  z   y  z  0.5    Điểm toàn bài tự luận (14 điểm) Tổng điểm toàn bài : 20 điểm Lưu ý khi chấm bài: - Trên đây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp logic. Nếu học sinh trình bày cách làm khác mà đúng thì cho điểm các phần theo thang điểm tương ứng. - Với bài 4phần tự luận, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không chấm.