PHÒNG GD& ĐT THANH BA
TRƯỜNG THCS ĐẠI AN
ĐỀ CHÍNH THỨC
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2019 - 2020
MÔN: TOÁN - LỚP 9
Thời gian làm bài: 120 phút không kể thời gian giao đề
Bài 1: (4,0 điểm)
Cho biểu thức
1 1 2x x 1 2x x x x
A:
1x
1 x x 1 x x







Với
1
x 0; x ; x 1
4
a) Rút gọn biểu thức A.
b) Tính giá trị của A khi
x 17 12 2
c) So sánh A với
A
.
Bài 2: (4,0 điểm)
a) Cho x + y = 1. Tìm giá trị nhỏ nhất của biểu thức M = x3 + y3
b) Chứng minh rằng:
Biểu thức
có giá trị là một số tự nhiên.
Bài 3: (4,0 điểm)
a) Giải phương trình
22
x 3x 2 x 3 x 2 x 2x 3
b) Cho 3 số thỏa mãn điều kiện:
x2+2y+1 = y2+2z+1 = z2+2x+1 = 0
Hãy tính giá trị của biểu thức: A = x2012 + y2012 + z2012
Bài 4.(7,0 điểm)
Cho tam giác ABC có AB = c; AC = b; BC = a, phân giác AD
a) Chứng minh hệ thức AD2 = AB.AC – BD.DC
b) Tính độ dài phân giác AD?
Bài 5: (1,0 điểm) Rút gọn biểu thức sau:
1 1 1 1
............
1 2 2 3 3 4 2009 2010
A
----- Hết -----
HƯỚNG DẪN CHẤM THI
HỌC SINH GIỎI CẤP TRƯỜNG NĂM HỌC 2019-2020
MÔN TOÁN LỚP 9
Bài 1 (4 điểm)
a) Rút gọn biểu thức (2 điểm)
1 1 2x x 1 2x x x x 1
A : x 0;x ;x 1
1 x 4
1 x x 1 x x

 














x 2x x 1
x 1 x 2x 2 x x 1
:
x 1 x 1 x 1 x 1 x 1 x x





x 1 2 x 1 x x 1 2 x 1
2 x 1 :
x x 1 1 x 1 x 1 x 1 x x
2 x 1 1 x
: 2 x 1 1 x 1 x x
x x 1








1 x x x 1 x
2 x 1 : 2 x 1 :
x x 1 1 x 1 x x

1 1 1 x x
:x
x x 1 1 x 1 x x


0.5
0.5
0.25
0.25
0.5
b) Tính giá trị của A khi
x 17 12 2
(1 điểm).
Tính
22
x 17 12 2 3 2 2 x 3 2 2 3 2 2 3 2 2
1 3 2 2 17 12 2 5 3 2 2
15 10 2
A5
3 2 2 3 2 2 3 2 2
0.5
0.5
c) So sánh A với
A
(1 điểm).
Biến đổi
1 x x 1
A x 1
xx

Chứng minh được
1
x2
x

với mọi
1
x 0;x ;x 1
4
1
A x 1 1 A 1 A 1 0 A A 1 0
x
A A 0 A A
0.25
0.25
0.5
Bài 2 (4 điểm)
a) Ta có M = x3 + y3 = (x + y)(x2 - xy + y2) = x2 - xy + y2 ( vì x + y = 1)
0.25
M =
2 2 2 2
2 2 2
1( ) ( )
2 2 2 2 2 22
x y x y x y
xy x y
Suy ra M
22
1()
2xy
Mặt khác : x + y =1
x2 + y2 +2xy = 1
2(x2 + y2) – (x – y )2 = 1
2(x2 + y2)
1
Do đó : x2 + y2
1
2
Dấu “ = “ xảy ra khi và chỉ khi x = y =
1
2
Ta có M
22
1()
2xy
và x2 + y2
1
2
M
1 1 1
2 2 4
Vậy M
1
4
, nên giá trị nhỏ nhất của biểu thức M bằng
1
4
khi x = y =
1
2
0.5
0.25
0.5
0.25
0.25
b) Biểu thức
2
2
2
2008 2008
B 1 2008 2009 2009
có giá trị là một số tự nhiên ).
Ta có :
22
2
2
22
2008 2008 2008 2008
B 1 2008 1 2008 2.1.2008
2009 2009 2009 2009
.
2
2
2
2
2008 2008 2008 2008 2008
2009 2.2009. 2009
2009 2009 2009 2009 2009



.
2008 2008 2008 2008
2009 2009 2009
2009 2009 2009 2009
.
Vậy B có giá trị là một số tự nhiên.
0.75
0.75
0.5
Bài 3 (4điểm) Giải phương trình
a)
22
x 3x 2 x 3 x 2 x 2x 3
x 1 x 2 x 3 x 2 x 1 x 3 1
Điều kiện
x 1 x 2 0
x 3 0 x2
x 2 0
x 1 x 3 0



1 x 2 x 1 1 x 3 x 1 1 0
x 1 1 0 x 1 1
x 1 1 x 2 x 3 0 x 2
x 2 x 3 0 x 2 x 3




x = 2 thoả mãn điều kiện xác định. Vậy phương trình có nghiệm duy nhất x = 2.
0.5
0.25
0.25
0.5
0.5
b).Ta có x2+2y+1 = 0 (1); y2+2z+1 = 0 (2)
z2+2x+1 = 0 (3)
0.25
Cộng từng vế của (1),(2),(3) ta có
(x2+2x+1) +( y2+2y+1) + (z2+2z+1) = 0
2 2 2
( 1) ( 1) ( 1) 0
10
11
10
x y z
x
y x y z
z


Vậy: A = x2012 + y2012 + z2012 = (-1)2012+(-1)2012+(-1)2012 = 3
0.5
0.75
0.5
Bài 4 (7 điểm)
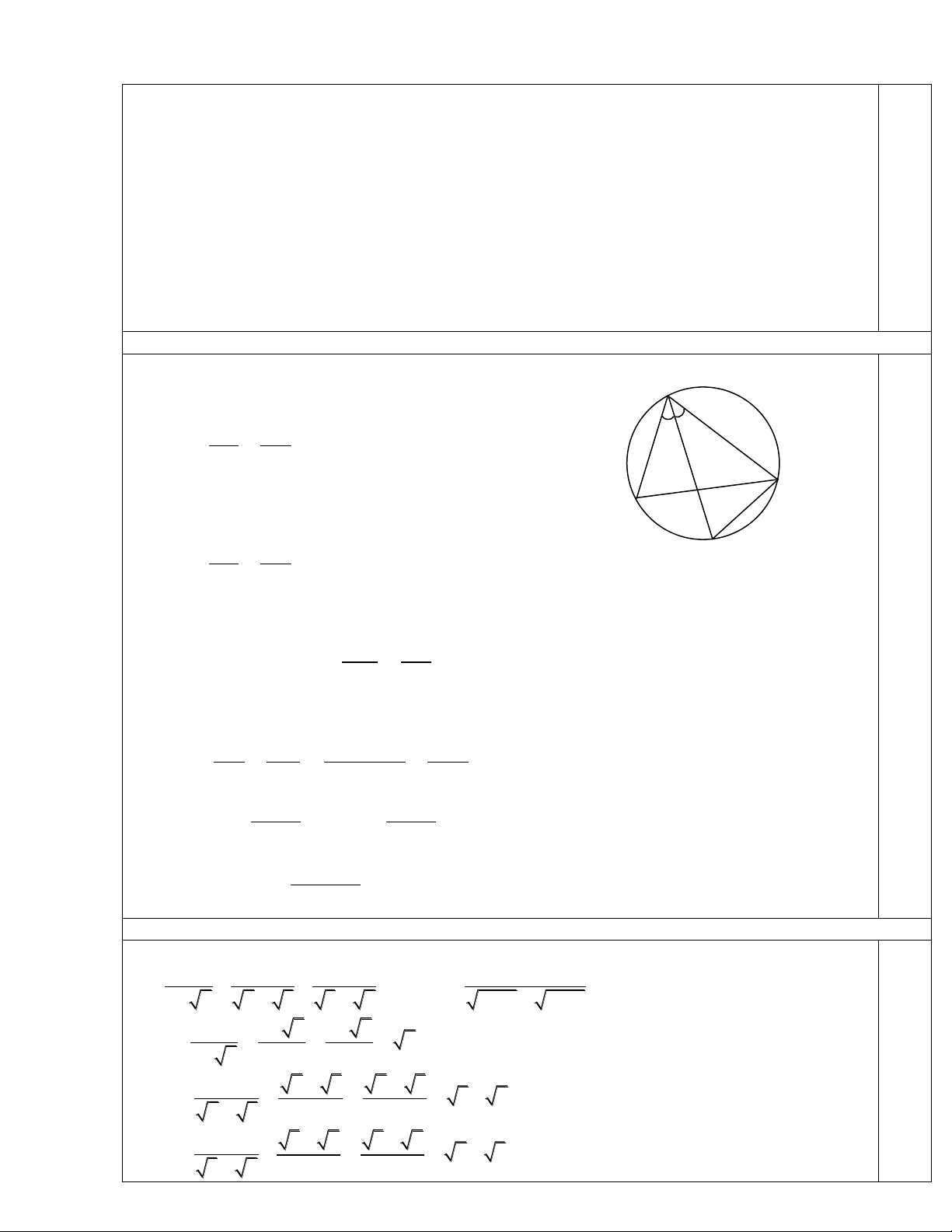
Vẽ đường tròn tâm O ngoại tiếp
ABC
Gọi E là giao điểm của AD và (O)
a) Ta có :
ABD ~
CED (g –g)
CD
AD
ED
BD
AD.ED = BD.CD
AD(AE – AD) = BD.CD
AD2 = AD.AE – BD.CD (1)
Lại có:
ABD ~
AEC (g –g)
AC
AD
AE
AB
AB.AC = AD.AE (2)
Từ (1) và (2) suy ra: AD2 = AB.AC – BD.DC
b) Vì AD là phân giác
CA
BA
DC
DB
b
DC
c
DB
cb
a
bc
DCDB
DB =
cb
ac
và DC =
cb
ab
AD2 = bc -
2
2
)( cb
bca
0.5
0.5
1
0.5
0.5
0.5
1
0.5
0.5
0.5
1
Bài 5 (1,0 điểm)
Rút gọn biểu thức sau:
1 1 1 1
............
1 2 2 3 3 4 2009 2010
A
Ta có:
1 1 2 1 2 21
1 2 1
12


1 2 3 2 3 32
2 3 1
23


1
34
=
3 4 3 4 43
4 3 1


0.5
A
B
C
E
D
Tương tự ta có
1 1 1 1
............
1 2 2 3 3 4 2009 2010
A
=
2 1 3 2 4 3 ... 2010 2009
(
=
1 2010 2010 1
0.25
0.25
Chú ý: . Nếu thí sinh làm bài bằng cách khác đúng thì vẫn cho điểm tương đương.