S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
QU NG TRẢ Ị
Đ THI CHÍNH TH CỀ Ứ
K THI CH N H C SINH GI I VĂN HÓA L P 12Ỳ Ọ Ọ Ỏ Ớ
THPT
Khóa ngày 02 tháng 10 năm 2018
Môn thi: TOÁN
Th i gian làm bài: 180 phút, không k th i gianờ ể ờ
giao đề
Câu 1. (3,0 đi m)ể Cho hàm s Tìm t t c các giá tr c a tham s ố ấ ả ị ủ ố đ hàm s ngh chể ố ị
bi n trong kho ng ế ả
Câu 2. (4,0 đi m)ể
1. Gi i ph ng trình: ả ươ
2. Gi i h ph ng trình: ả ệ ươ
Câu 3. (2,0 đi m) ểCho là các s th c d ng th a mãn Tìm giá tr nh nh t c a bi uố ự ươ ỏ ị ỏ ấ ủ ể
th c ứ
Câu 4. (2,0 đi m)ể B n An v lên gi y m t đa giác l i có s c nh nhi u h n 4. Sau đóạ ẽ ấ ộ ồ ố ạ ề ơ
b n An đm các tam giác nh n đnh c a đa giác làm đnh và nh n xét: s tam giácạ ế ậ ỉ ủ ỉ ậ ố
không có c nh chung v i nhi u g p 5 l n s tam giác có đúng m t c nh chung v i H iạ ớ ề ấ ầ ố ộ ạ ớ ỏ
b n An v đa giác l i có bao nhiêu c nh?ạ ẽ ồ ạ
Câu 5. (6,0 đi m)ể
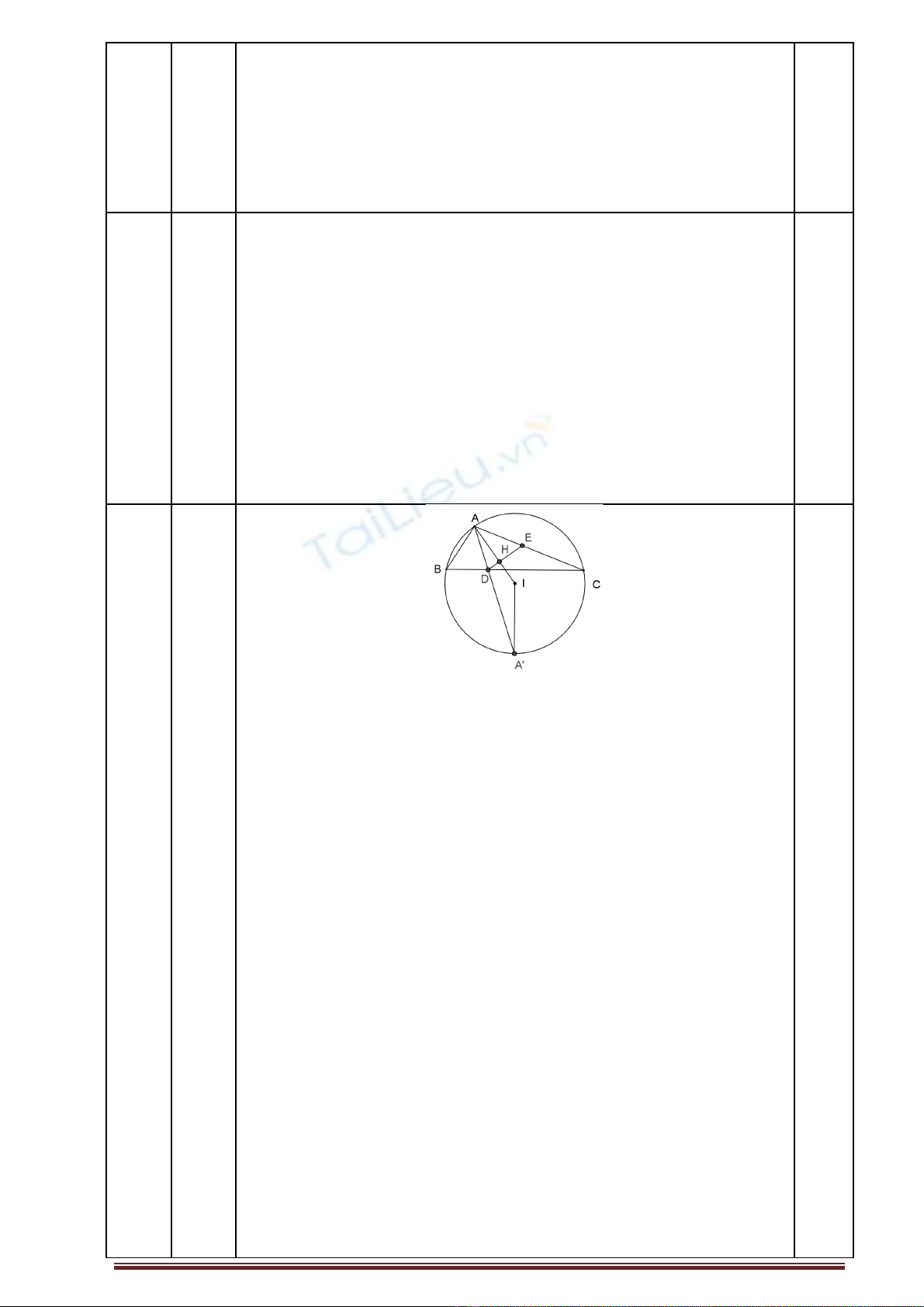
1. Trong m t ph ng t a đcho tam giácG i là chân đng phân giác trong gócặ ẳ ọ ộ ọ ườ
là m t đi m thu c đo n th a mãn Tìm t a đ các đnh bi t ph ng trình đng trònộ ể ộ ạ ỏ ọ ộ ỉ ế ươ ườ
ngo i ti p tam giác là và có hoành đ d ng.ạ ế ộ ươ
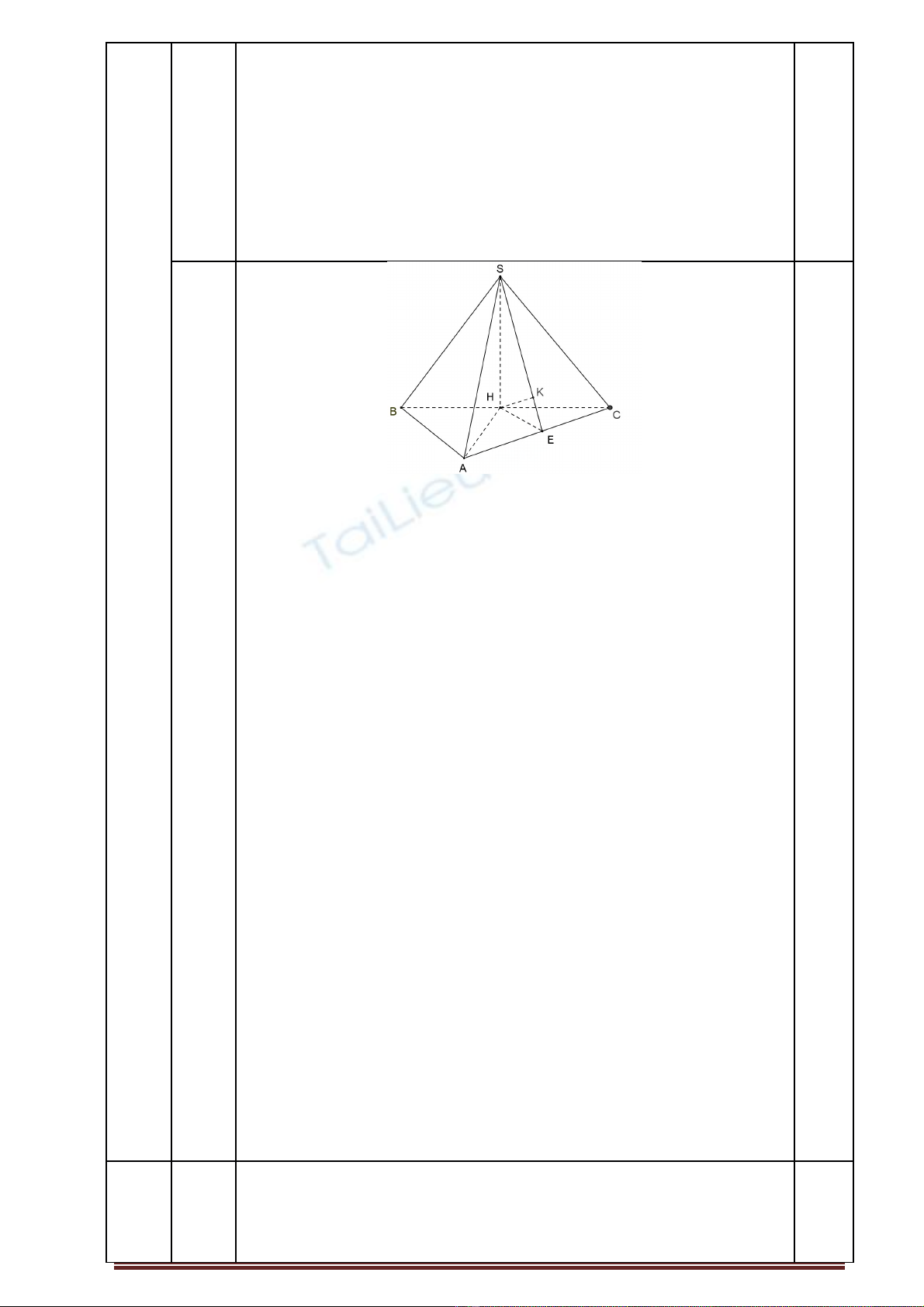
2. Cho hình chóp có đáy là tam giác vuông t i ạG i là hình chi u vuông góc c aọ ế ủ
trên Bi t vuông góc v i m t ph ng ế ớ ặ ẳ và t o v i m t ph ng m t góc Tính th tíchạ ớ ặ ẳ ộ ể
kh i chóp ố và tính kho ng cách t ả ừ đn m t ph ng ế ặ ẳ theo
Câu 6. (3,0 đi m)ể Cho dãy s bi tố ế
1. V i , ch ng minh r ng dãy có gi i h n h u h n và tìm gi i h n đó.ớ ứ ằ ớ ạ ữ ạ ớ ạ
2. Ch ng minh r ng v i m i , dãy có gi i h n h u h n.ứ ằ ớ ọ ớ ạ ữ ạ
--------- H T ---------Ế
(Thí sinh không đc s d ng tài li u và máy tính c m tay)ượ ử ụ ệ ầ
H NG D N CH MƯỚ Ẫ Ấ
Đ THI CH N H C SINH GI I VĂN HÓA L P 12 THPT NĂM H C 2018 - 2019Ề Ọ Ọ Ỏ Ớ Ọ
Môn thi: TOÁN
CâuÝN i dungộĐiể
m
1
(3,0đ
)
Ta có
Hàm s ngh ch bi n trong kho ng ố ị ế ả
Xét hàm s trên kho ng ố ả
Ta có
T b ng bi n thiên suy ra ừ ả ế
0,5
0,5
0,5
0,5
0,5
0,5
2
(4,0đ
)
1
(1,0đ)
Gi i: Đi u ki n: ả ề ệ
Ph ng trình đã cho t ng đng v i ươ ươ ươ ớ
Đt ta có , ặ
Ph ng trình tr thành: ươ ở
V i ta có Ph ng trình vô nghi m do ớ ươ ệ
V i ta có ớ
V y ph ng trình có nghi m ậ ươ ệ
0,5
0,5
0,5
0,5
Đi u ki n: ề ệ
Xét hàm s ta có , hàm s đng bi n trên nên t ta có ố ố ồ ế ừ
Th vào ta có ph ng trình:ế ươ
( đi u ki n )ề ệ
2
(2,0đ)
V i ta có ớ
Do đó ph ng trình vô nghi m, ph ng trình có hai nghi m ươ ệ ươ ệ
V y h ph ng trình có hai nghi m ậ ệ ươ ệ
0,5
0,5
0,5
0,5
3
(2,0đ
)
T ng t ta có ươ ự
Xét
L p b ng bi n thiên và t đó suy ra ậ ả ế ừ
Ta có d u đng th c x y ra khi ấ ẳ ứ ả
V y ậ
0,5
0,5
0,5
0,5
4
(2,0đ
)
G i là s c nh c a đa giác.ọ ố ạ ủ
S tam giác có 3 đnh là đnh c a đa giác ố ỉ ỉ ủ
S tam giác có 3 đnh là đnh c a đa giác và có 1 c nh chung v i (H) làố ỉ ỉ ủ ạ ớ
S tam giác có 3 đnh là đnh c a đa giác và có 2 c nh chung v i (H) làố ỉ ỉ ủ ạ ớ
S tam giác có 3 đnh là đnh c a đa giác và không có c nh chung v i ố ỉ ỉ ủ ạ ớ
(H) là
Theo gi thi t ả ế
Gi i ph ng trình này, ta đc ả ươ ượ
0,5
0,5
0,5
0,5
1
(3,0đ)
G i ọ
Ta có và chung nên
Ta có
Suy ra
Đng tròn ngo i ti p tam giác có tâm ườ ạ ế
Ph ng trình đng th ng ươ ườ ẳ
T a đ là nghi m c a h : ọ ộ ệ ủ ệ
Do có hoành đ d ng nên ộ ươ
Ph ng trình đng th ng ươ ườ ẳ
G i là giao đi m th 2 c a và đng tròn ọ ể ứ ủ ườ
Ph ng trình đng th ng ươ ườ ẳ
T a đ là nghi m c a h ọ ộ ệ ủ ệ
Suy ra
Do nên
1,0
0,5
0,5
5
(6,0đ
)
0,5
0,5
2
(3,0đ)
Góc gi a và là suy ra ữ
Ta có
Ta có
H ta có m t khác ạ ặ
suy ra V y ậ
Ta có và
V y ậ
0,5
0,5
0,5
0,5
0,5
0,5
Ta có
khi
khi
Do đó n u thì . Do nên ế