Thông qua việc giải trực tiếp trên “Đề thi KSCL đầu năm môn Toán lớp 12 năm 2024-2025 - Trường THPT Lê Văn Thịnh, Bắc Ninh” các em sẽ nắm vững nội dung bài học, rèn luyện kỹ năng giải đề, hãy tham khảo và ôn thi thật tốt nhé! Chúc các em ôn tập kiểm tra đạt kết quả cao!
AMBIENT/
Chủ đề:
Nội dung Text: Đề thi KSCL đầu năm môn Toán lớp 12 năm 2024-2025 - Trường THPT Lê Văn Thịnh, Bắc Ninh
- SỞ GD &ĐT BẮC NINH ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
TRƯỜNG THPT LÊ VĂN THỊNH NĂM HỌC 2024-2025
(Đề thi gồm 04 trang )
Môn: Toán Khối: 12
Ngày thi: 15 tháng 9 năm 2024
Thời gian làm bài:90 phút (không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ...................
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Tập nghiệm của bất phương trình là
A. . B. .
C. . D. .
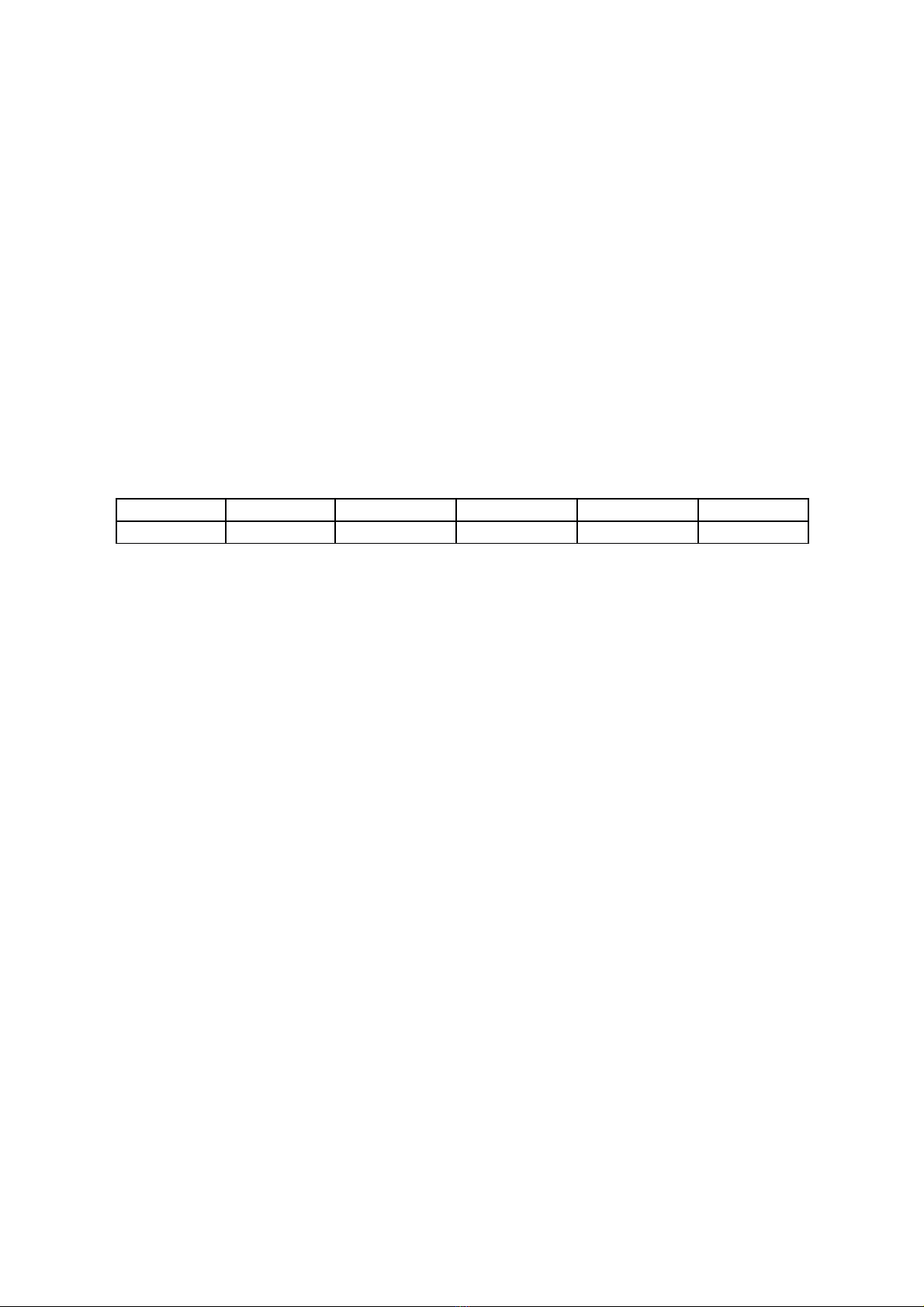
Câu 2. Điểm khảo sát đầu năm môn Toán của lớp 12B được cho dưới bảng số liệu ghép nhóm sau:
Điểm
Số học sinh 1 3 13 18 10
Giá trị đại diện của nhóm là
A. . B. . C. . D. .
Câu 3. Hình ảnh đường cong dưới đây là dạng đồ thị của hàm số
A. . B. . C. . D. .
Câu 4. Biểu thức xác định khi
A. . B. . C. . D. .
Câu 5. Đồ thị hàm số có điểm cực đại là
A. . B. . C. . D. .
Câu 6. Đạo hàm của hàm số bằng
A. . B. . C. . D. .
Câu 7. Cho hàm số có bảng biến thiên:
Giá trị lớn nhất của hàm số trên đoạn là
A. . B. . C. . D. .
Câu 8. Đồ thị hàm số có tiệm cận ngang là đường thẳng
A. . B. . C. . D. .
Câu 9. Một đội bóng có 7 cầu thủ có thể thi đấu ở vị trí thủ môn. Để chuẩn bị cho một trận đấu giao lưu,
huấn luyện viên dự định chọn ngẫu nghiên 2 cầu thủ thay nhau thi đấu ở vị trí thủ môn. Số cách chọn 2 thủ
môn là
A. . B. . C. . D. .
Câu 10. Cho hàm số có đồ thị như hình vẽ
Hàm số đồng biến trên khoảng
A. . B. . C. . D. .
Câu 11. Cho cấp số cộng có . Số hạng bằng
1/3 - Mã đề 215
- A. . B. . C. . D. .
Câu 12. Giới hạn bằng
A. . B. . C. . D. .
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG – SAI.
Học sinh trả lời từ câu 13 đến câu 16. Mỗi ý thí sinh chỉ được phép chọn đúng hoặc sai.
Câu 13. Cho hàm số . Trong các mệnh đề sau, mệnh đề nào đúng, mệnh để nào sai?
A. Đồ thị hàm số không có giao điểm với trục hoành.
B. Hàm số có một điểm cực đại và một điểm cực tiểu.
C. .
D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng .
Câu 14. Cho hình chóp có đáy là hình chữ nhật, , đường thẳng vuông góc với mặt phẳng và .
Trong các mệnh đề sau, mệnh đề nào đúng, mệnh để nào sai?
A. Khoảng cách từ điểm đến mặt phẳng bằng: , ( nguyên dương và tối giản). Khi đó: .
B. Góc giữa đường thẳng và mặt phẳng bằng: , ( nguyên dương và tối giản). Khi đó: .
C. Tan góc giữa hai mặt phẳng và là: .
D. Thể tích khối chóp là : .
Câu 15. Cho hàm số .
Trong các mệnh đề sau, mệnh đề nào đúng, mệnh để nào sai?
A. Phương trình có nghiệm là: .
B. Tập xác định của hàm số là : .
C. Bất phương trình có số nghiệm nguyên là: .
D. Ta có: .
Câu 16. Quãng đường chuyển động của một vật được tính theo thời gian bởi công thức, với là khoảng thời
gian tính bằng giờ kể từ khi vật bắt đầu chuyển động. Trong các mệnh đề sau, mệnh đề nào đúng, mệnh đề
nào sai?
A. Vật chuyển động chậm dần trong khoảng thời gian từ giờ đến giờ kể từ khi bắt đầu chuyển động.
B. Vận tốc tức thời của chuyển động luôn lớn hơn .
C. Tại thời điểm giờ, vật quay về vị trí xuất phát (quãng đường bằng ) và kể từ đó, quãng đường chuyển
động của vật luôn tăng theo thời gian.
D. Quãng đường mà vật chuyển động được tại thời điểm phút là .
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Học sinh trả lời từ câu 17 đến câu 22.
Câu 17. Hàm số nghịch biến trên khoảng , trong đó là số nguyên dương. Khi đó bằng:
Câu 18. Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là
hình vuông và diện tích bề mặt bằng như hình vẽ. Tìm chiều cao của chiếc hộp sao cho thể tích của chiếc
hộp là lớn nhất.
Câu 19. Cho hàm số có đạo hàm liên tục trên và có bảng xét dấu của như sau
Hỏi hàm số có bao nhiêu điểm cực đại?
Câu 20. Cho hàm số liên tục trên và có đồ thị như hình vẽ
Đặt . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn bằng (trong đó nguyên dương và tối
giản). Tính .
Câu 21. Có bao nhiêu số nguyên thoả mãn
2/3 - Mã đề 215
- Câu 22. Cho khối chóp có đáy là hình chữ nhật vuông góc với mặt đáy và tạo với mặt phẳng một góc .
Thể tích của khối chóp đã cho bằng
( nguyên dương và tối giản). Tính .
------ HẾT ------
3/3 - Mã đề 215
Thêm vào BST
Báo xấu
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
