WWW.VNMATH.COM
Đ s 5ề ố
Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
Câu 1:
1) Gi i các b t ph ng trình sau: ả ấ ươ
a)
x x4 3 2+ ≥ +
b)
x
x
2 5 1
2
−≥
−
2) Cho các s ốa, b, c ≥ 0. Ch ng minh: ứ
bc ca ab a b c
a b c
+ + ≥ + +
Câu 2: Cho ph ng trình: ươ
x x m m
2 2
2 4 3 0− − + − + =
a) Ch ng minh ph ng trình luôn có nghi mứ ươ ệ
b) Tìm m đ ph ng trình có 2 nghi m trái d uể ươ ệ ấ
Câu 3:
a) Ch ng minh đ ng th c sau:ứ ẳ ứ
3 2
3
sin cos tan tan tan 1
cos
α α α α α
α
+= + + +
b) Cho sina + cosa =
1
3
−
. Tính sina.cosa
Câu 4 : Đi m thi c a 32 h c sinh trong kì thi Ti ng Anh (thang đi m 100) nh sau :ể ủ ọ ế ể ư
68 79 65 85 52 81 55 65 49 42 68 66 56 57 65 72
69 60 50 63 74 88 78 95 41 87 61 72 59 47 90 74
a) Hãy trình bày s li u trên d i d ng b ng phân b t n s , t n su t ghép l p v i các l p:ố ệ ướ ạ ả ố ầ ố ầ ấ ớ ớ ớ
) ) ) ) )
40;50 ; 50;60 ; 60;70 ; 70;80 ; 80;90 ; 90;100
.
b) Nêu nh n xét v đi m thi c a 32 h c sinh trong kì thi Ti ng Anh k trên ?ậ ề ể ủ ọ ế ể
c) Hãy tính s trung bình c ng, ph ng sai, đ l ch chu n c a các s li u th ng kê đã cho?ố ộ ươ ộ ệ ẩ ủ ố ệ ố
(Chính xác đ n hàng ph n trăm ).ế ầ
d) Hãy v bi u đ t n su t hình c t đ mô t b ng phân b t n su t ghép l p đã l p câuẽ ể ồ ầ ấ ộ ể ả ả ố ầ ấ ớ ậ ở
a).
Câu 5:
a) Cho đ ng th ng d: ườ ẳ
và đi m A(3; 1). Tìm ph ng trình t ng quát c aể ươ ổ ủ
đ ng th ng (ườ ẳ ∆) qua A và vuông góc v i d.ớ
b) Vi t ph ng trình đ ng tròn có tâm B(3; –2) và ti p xúc v i (ế ươ ườ ế ớ ∆′ ): 5x – 2y + 10 = 0.
c) L p chính t c c a elip (E), bi t m t tiêu đi m c a (E) là Fậ ắ ủ ế ộ ể ủ 1(–8; 0) và đi m M(5; –3ể
3
)
thu c elip.ộ
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
WWW.VNMATH.COM
Đ s 5ề ố
ĐÁP ÁN Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
Câu 1:
1) Gi i các b t ph ng trình sau: ả ấ ươ
a)
x x x x x x x x
2 2 2
4 3 2 16 24 9 4 4 15 20 5 0+ ≥ + ⇔ + + ≥ + + ⇔ + + ≥
x1
( ; 1] ;
3
⇔ ∈ −∞ − ∪ − +∞÷
b)
x x x x x
x x x x
2 5 2 5 2 5 3 7 7
1 1 0 1 0 0 2;
2 2 2 2 3
− − − −
≥ ⇔ − ≥ ⇔ + ≤ ⇔ ≤ ⇔ ∈
− − − −
2) Vì a, b, c ≥ 0 nên các s ố
ab cb ca
c a b
, ,
đ u d ng. ề ươ
Áp d ng BĐT Cô-si ta có:ụ
ca ab ca ab a a
b c b c
cb ab cb ab b b
a c a c
bc ca bc ca c c
a b a b
2
2
2
2 . 2 2
2 . 2 2
2 . 2 2
+ ≥ = =
+ ≥ = =
+ ≥ = =
C ng các b t đ ng th c trên, v theo v , ta đ c b t đ ng th c c n ch ng minh.ộ ấ ẳ ứ ế ế ượ ấ ẳ ứ ầ ứ
D u b ng x y ra khi và ch khi ấ ằ ả ỉ a = b = c.
Câu 2: Cho ph ng trình: ươ
x x m m
2 2
2 4 3 0− − + − + =
x x m m
2 2
2 4 3 0⇔ + − + − =
a)
m m m m m m R
2 2 2
' 1 4 3 4 4 ( 2) 0,
∆
= + − + = − + = − ≥ ∀ ∈
⇒ PT đã cho luôn có nghi m v i m i ệ ớ ọ m
b) PT có hai nghi m trái d u ệ ấ ⇔ ac < 0
m m m
24 3 0 ( ;1) (3; )⇔ − + − < ⇔ ∈ −∞ ∪ +∞
Câu 3:
a)
2 2
3 2 2
sin cos sin 1 1
. tan (1 tan ) 1 tan
cos
cos cos cos
α α α α α α
α
α α α
+= + = + + +
2 3
1 tan tan tan
α α α
= + + +
b)
1 1 8 4
sin cos 1 2sin cos 2sin cos sin cos
3 9 9 9
α α α α α α α α
−
+ = − ⇔ + = ⇔ = ⇔ = −
Câu 4:
2
L p đi mớ ể
T n sầ ố
ni
T n su tầ ấ
fi
Giá trị
đ i di nạ ệ
ci
[40;50) 4 13% 45 180 8100
[50;60) 6 19% 55 330 18150 S trung bình c ng:ố ộ 66,88
[60;70) 10 31% 65 650 42250 Ph ng sai:ươ 190,23
[70;80) 6 19% 75 450 33750 Đ l ch chu n:ộ ệ ẩ 13,79
[80;90) 4 13% 85 340 28900
[90;100] 2 6% 95 190 18050
N 32 100% 2140 149200
i i
n c
i i
n c
2
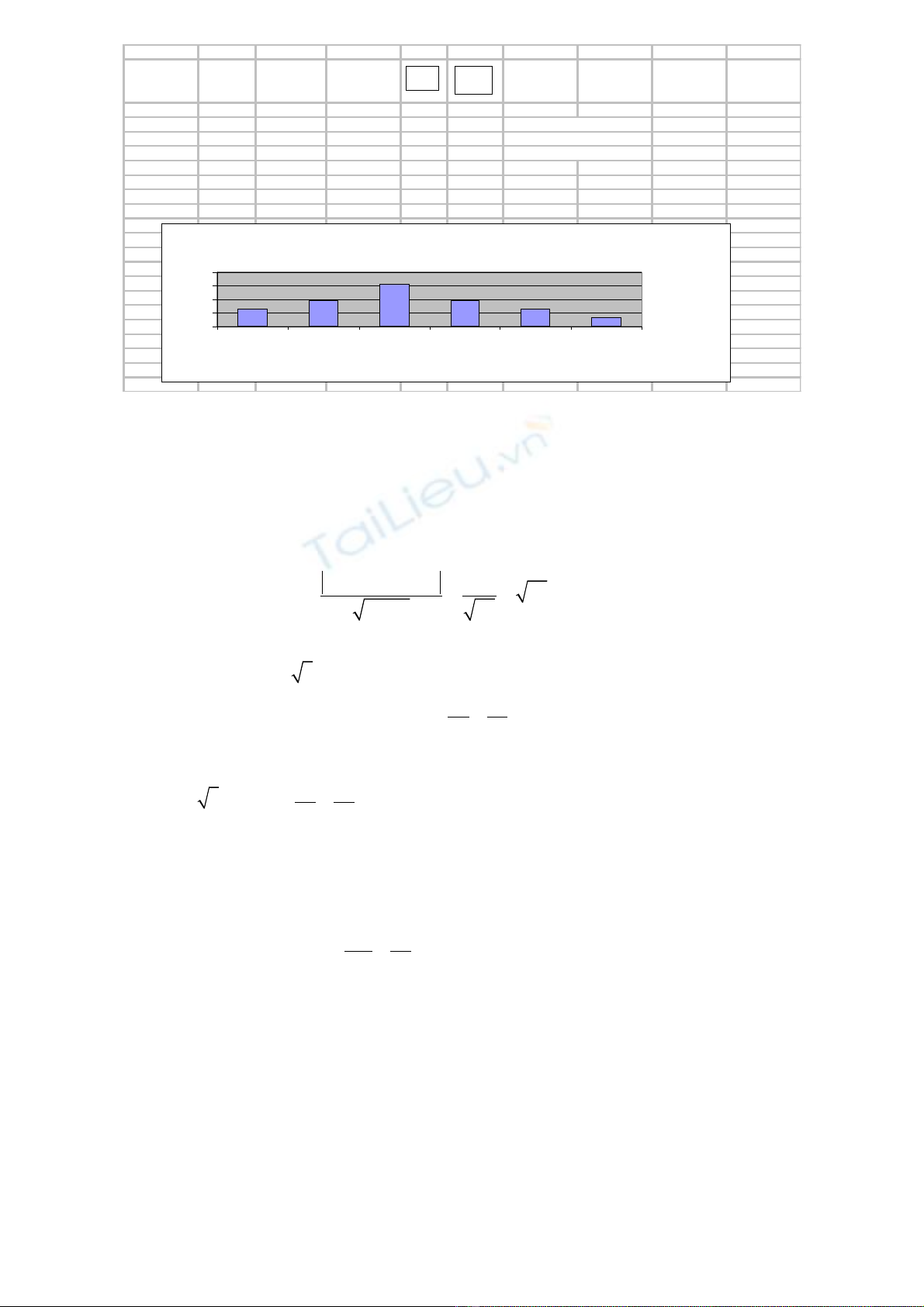
B ng phân b t n su t Đi m thi môn Ti ng Anhả ố ầ ấ ể ế
6%
13%
19%
31%
19%
13%
0%
10%
20%
30%
40%
[40;50) [50;60) [60;70) [70;80) [80;90) [90;100]
Đi mể
Câu 5:
a) Cho đ ng th ng d: ườ ẳ
và đi m A(3; 1). ể
• d có VTCP
u( 2;2)= −
r
• (∆) ⊥ d nên
u( 2;2)= −
r
cũng là VTPT c a (ủ∆)
• Ph ng trình t ng quát c a (ươ ổ ủ ∆) là
x y x y2( 3) 2( 1) 0 2 0− − + − = ⇔ − − =
b) B(3; –2), (∆′ ): 5x – 2y + 10 = 0.
• Bán kính
R d B 5.3 2( 2) 10 29
( , ) 29
25 4 29
∆
− − +
′
= = = =
+
• V y ph ng trình đ ng tròn: ậ ươ ườ
x y
2 2
( 3) ( 2) 29− + + =
c) F1(–8; 0) , M(5;
3 3−
)
• Ph ng trình chính t c c a (E) có d ng ươ ắ ủ ạ
x y
a b
2 2
2 2
1 (1)+ =
• Vì (E) có m t tiêu đi m là ộ ể
F
1( 8;0)−
nên ta có c = 8 và
a b c a b
2 2 2 2 2 64= + ⇔ = +
•
M E a b a b
a b
2 2 2 2
2 2
25 27
(5; 3 3) ( ) 1 27 25− ∈ ⇒ + = ⇔ + =
• Gi i h ả ệ
a b
a b a b
2 2
2 2 2 2
64
27 25
= +
+ =
⇒
b b b b b b
2 2 2 2 4 2
27( 64) 25 ( 64) 12 1728 0+ + = + ⇔ + − =
⇔
b236=
(
a2100=
)
V y ph ng trình Elip là ậ ươ
x y
2 2 1
100 36
+ =
--------------------H t-------------------ế
3