ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)
Câu I (2 điểm) Cho hàm số 4 2
2 1
y x mx m
(1) , với
m
là tham số thực.
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi
1
m
.
2. Xác định
m
để hàm số (1) có ba điểm cực trị, đồng thời các điểm cực trị của đồ thị
tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng
1
.
Câu II (2 điểm) 1.Giải phương trình tan4x +1 = 2
4
(2 sin 2 )sin3
os
c x
.
2. Giải hệ phương trình sau:
3
1
2
7
)(
3
)(44 2
22
yx
x
yx
yxxy
Câu III (1 điểm) Tính tích phân: I = 2
3
0
sinxdx
(sinx + cosx)
Câu IV (1 điểm) Tính thể tích của hình chóp S.ABC, biết đáy ABC là một tam giác đều cạnh a, mặt bên
( SAB) vuông góc với đáy, hai mặt bên còn lạ cùng tạo với đáy một góc
.
Câu V (1 điểm)
Chứng minh rằng với mọi số tự nhiên n ( với n
2), ta có: ln2n > ln(n-1).ln(n+1)
II. PHẦN RIÊNG (3 điểm)
Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc 2)
1. Theo chương trình Chuẩn
Câu VI.a (1 điểm) Trong mặt phẳng với hệ toạ độ
Ox
y
, tìm điểm
A
thuộc trục hoành và điểm
B
thuộc
trục tung sao cho
A
và
B
đối xứng với nhau qua đường thẳng
:2 3 0
d x y
.
Câu VII.a (1 điểm)
Tìm số hạng không chứa
x
trong khai triển nhị thức Niutơn của
18
5
1
2 0
x x
x
.
Câu VIII.a (1 điểm) Giải bất phương trình log5(3+
x
) > 4
log
x
.
2. Theo chương trình Nâng cao.
Câu VI.b (1 điểm) Trong mặt phẳng với hệ toạ độ
Ox
y
cho tam giác
ABC
vuông ở
A
. Biết
1;4 , 1; 4
A B
và đường thẳng
BC
đi qua điểm
1
2;
2
M
. Hãy tìm toạ độ đỉnh
C
.
Câu VII.b (1 điểm) Tìm hệ số của
8
x
trong khai triển nhị thức Niutơn của
2
2
n
x, biết
3 2 1
8 49
n n n
A C C
.
(
k
n
A
là số chỉnh hợp chập
k
của
n
phần tử,
k
n
C
là số tổ hợp chập
k
của
n
phần tử).
Câu VIII.b (1 điểm) Cho hàm số
2
4 3
2
x x
y
x
. Chứng minh rằng tích các khoảng cách từ một
điểm bất kỳ trên đồ thị hàm số đến hai đường tiệm cận của nó luôn là một hằng số.
----------------------------------Hết----------------------------------
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG
Câu Nội dung Điể
m
I (2điểm) 1.(1 điểm). Khi
1
m
hàm số trở thành:
4 2
2
y x x
TXĐ: D=
Sự biến thiên:
' 3 2
0
4 4 0 4 1 0
1
x
y x x x x x
0.25
0 0, 1 1
CD CT
y y y y
0.25
Bảng biến thiên
x -
-1 0 1 +
y’
0 + 0
0 +
y +
0 +
-1 -1
0.25
Đồ thị 0.25
2. (1 điểm)
' 3 2
2
0
4 4 4 0 x
y x mx x x m
x m
Hàm số đã cho có ba điểm cực trị
pt '
0
y
có ba nghiệm phân biệt và
'
y
đổi dấu
khi
x
đi qua các nghiệm đó
0
m
0.25
Khi đó ba điểm cực trị của đồ thị hàm số là:
2 2
0; 1 , ; 1 , ; 1
A m B m m m C m m m
0.25
2
1.
2
ABC B A C B
S y y x x m m
; 4, 2
AB AC m m BC m
0.25
4
3
2
1
2
. . 1 1 2 1 0
5 1
44
2
ABC
m
m m m
AB AC BC
R m m
Sm m m
0.25
II
(2điểm) 1 ( 1 điểm) ĐK: cosx
0
sinx
1.
Ta có phương trình
sin4x + cos4x = ( 2 – sin22x)sin3x
( 2 – sin22x)(1 – 2 sin3x) = 0
sin3x =
1
2
( do ( 2 – sin22x
1) 0.50
3sinx – 4sin3x =
1
2
. Thay sinx =
1 vào đều không thỏa mãn. 0.25
Vậy các nghiệm của PT là 2 5 2
; ( )
18 3 18 3
k k
x x k Z
0.25
2. (1 điểm) ĐK: x + y
0
Ta có hệ
2 2
2
3
3( ) ( ) 7
( )
13
x y x y x y
x y x y
x y
0.25
Đặt u = x + y +
1
x y
(
2
u
) ; v = x – y ta được hệ :
2 2
3 13
3
u v
u v
0.25
Giải hệ ta được u = 2, v = 1 do (
2
u
) 0.5
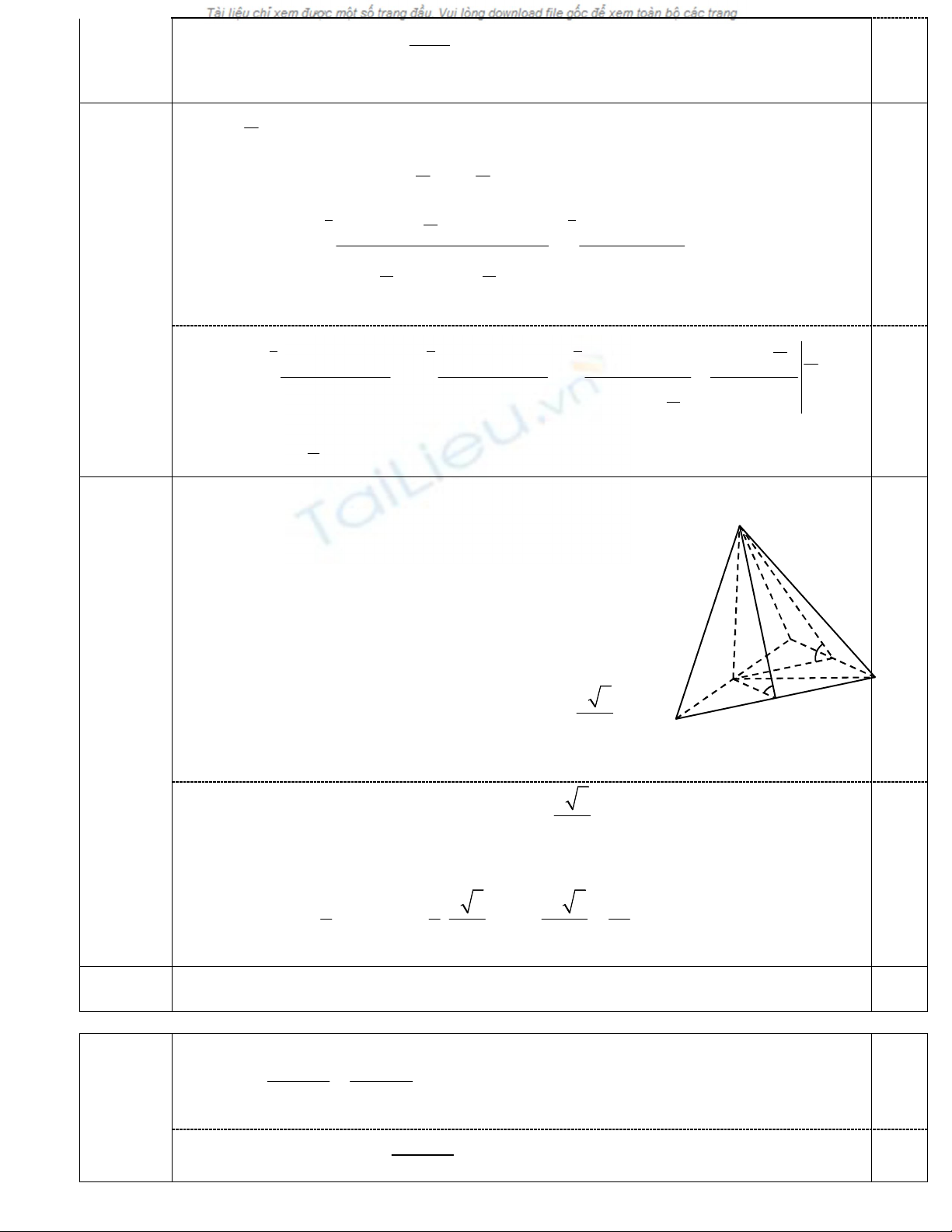
Từ đó giải hệ
12
1 1
1 0
1
x y x y x
x y x y y
x y
III
(1 điểm) Đặt x =
2
u
dx = - du
Đổi cận:
x = 0 u =
2
; x =
2
u = 0
Vậy: I =
2 2
3 3
0 0
sin( ) cosxdx
2
sinx +cosx
sin os
2 2
u du
u c u
0.50
Vậy : 2I =
2 2
2
2
0 0
sinx + cosx
(sinx + cosx)
sinx + cosx
dx
dx
= 2
2
0
tan 4
1
2
2
2 os 0
4
x
dx
c x
1
2
I
0.50
IV
(1 điểm)
Döïng
SH AB
Ta coù:
(SAB) (ABC), (SAB) (ABC) AB, SH (SAB)
SH (ABC)
vaø SH laø ñöôøng cao cuûa hình choùp.
Döïng
HN BC, HP AC
SN BC, SP AC SPH SNH
ΔSHN = ΔSHP HN = HP.
ΔAHP vuoâng coù: o
a 3
HP HA.sin60 .
4
0.50
ΔSHP vuoâng coù:
a 3
SH HP.tan tan
4
Theå tích hình choùp
2 3
ABC
1 1 a 3 a 3 a
S.ABC: V .SH.S . .tan . tan
3 3 4 4 16
0.50
V
(1 điểm)
Với n = 2 thì BĐT cần chứng minh đúng
0.25
Xét n > 2 khi đó ln(n – 1) > 0 BĐT tương đương với:
ln ln( 1)
ln( 1) ln
n n
n n
(1)
0.25
Hàm số f(x) = ln
ln( 1)
x
x
, với x > 2 là hàm nghịch biến, nên với n > 2 thì f(n) 0.50
S
H
P
C
A
B
N