B GIÁO D C VÀ ĐÀO T OỘ Ụ Ạ
GIÁO VIÊN: L I VĂN LONGẠ
Web: http://violet.vn/vanlonghanam
Đ 5Ề
Đ THI TH Đ I H C NĂM 2014Ề Ử Ạ Ọ
Môn thi: TOÁN – KH I A, A1, BỐ
Th i gian làm bài: 180 phút ,không k th i gian phát đờ ể ờ ề
I. PHÂN CHUNG CHO TÂT CA THI SINH (7,0 đi mể)
Câu 1. (2,0 đi mể). Cho hàm s ố
3 2 3
3 4y x mx m= − +
(1), v i m là tham s th c.ớ ố ự
a) Kh o sát s bi n thiên và v đ th c a hàm s (1) khi ả ự ế ẽ ồ ị ủ ố
1
=
m
.
b) Tìm m đ đ th hàm s (1) có hai đi m c c tr ể ồ ị ố ể ự ị A và B sao cho
2 2
20OA OB
+ =
.
Câu 2. (1,0 đi mể). Gi i ph ng trìnhả ươ
3 sin 2 os2 4 3(cos 3 sinx)x c x x
− + = +
.
Câu 3. (1,0 đi mể). Gi i h ph ng trình ả ệ ươ
( )
( ) ( )
2
1 2 17 0
4 32
x xy y
x y xy
+ + + − =
+ + =
Câu 4. (1,0 đi mể). Tính tích phân
( )
2
2
1
2ln
2
x x
I dx
x
+
=+
.
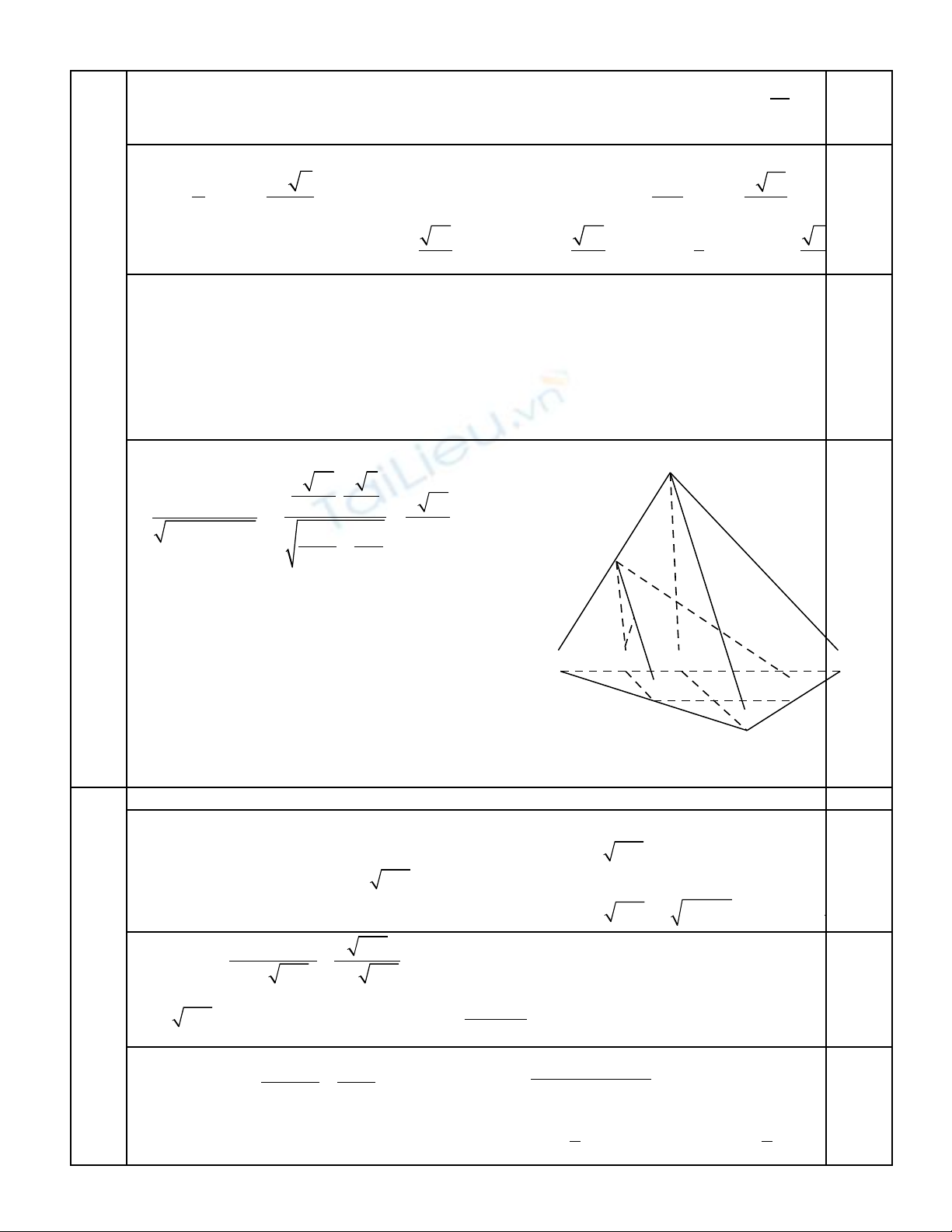
Câu 5. (1,0 đi mể). Cho hình chóp S.ABC có đáy là tam giác vuông cân t i ạB, BA = a. Tam giác SAC cân t i ạS
và n m trong m t ph ng vuông góc v i mpằ ặ ẳ ớ (ABC). G i ọM, N l n l t là trung đi m c a ầ ượ ể ủ SA, BC; bi t gócế
gi a ữMN v i mp(ABC) b ng ớ ằ
0
60
.Tính th tích kh i chóp ể ố S.ABC và kho ng cách gi a hai đ ng th ng chéoả ữ ườ ẳ
nhau AC, MN theo a.
Câu 6. (1,0 đi mể). Cho
, ,abc
là các s th c d ng và ố ự ươ
. Tìm giá tr l n nh t c a bi u th cị ớ ấ ủ ể ứ
( ) ( ) ( )
3
2
3 1 1 1
abc
Pab bc ca a b c
= +
+ + + + + +
II. PH N RIÊNG Ầ(3,0 đi mể) : Thí sinh ch đ c làm m t trong hai ph n riêng ỉ ượ ộ ầ (ph n A ho c ph n Bầ ặ ầ )
A. Theo ch ng trình Chu nươ ẩ
Câu 7.a (1,0 đi mể). Trong m t ph ng v i h t a đặ ẳ ớ ệ ọ ộ Oxy, cho hình ch nh t ữ ậ ABCD có di n tích b ng ệ ằ
12
.
Tâm I là giao đi m c a hai đ ng th ng ể ủ ườ ẳ
1
:d
3 0x y
− − =
và đ ng th ng ườ ẳ
2
:d
6 0x y
+ − =
. Trung đi m c aể ủ
c nh AD là giao đi m c a ạ ể ủ
1
d
v i tr c hoành. Xác đ nh t a đ b n đ nh c a hình ch nh t.ớ ụ ị ọ ộ ố ỉ ủ ữ ậ
Câu 8.a (1,0 đi mể). Trong không gian v i h toa đô ớ ệ Oxyz, cho đ ng th ng ườ ẳ d :
1 2
1 2 2
x y z
− +
= = −
. Tìm t aọ
đ đi m ộ ể M thu c đ ng th ng ộ ườ ẳ d sao cho m t c u ặ ầ (S) tâm M ti p xúc v i tr c ế ớ ụ Oz có bán kính b ng 2.ằ
Câu 9.a (1,0 đi mể). Cho s ph c z th a mãn ố ứ ỏ
2
1 2
zz
i
+ =
−
. Tìm ph n th c c a s ph c ầ ự ủ ố ứ
2
wz z
= −
B. Theo ch ng trình Nâng caoươ
Câu 7.b (1,0 đi mể). Trong m t ph ng t a đặ ẳ ọ ộ Oxy, cho đ ng tròn ườ
2 2
( ) : 2 4 5 0C x y x y+ − + − =
và đi mể
A(1;0). G i ọM, N là hai đi m trên đ ng tròn ể ườ (C) sao cho tam giác AMN vuông cân t i ạA. Vi t ph ng trìnhế ươ
c nh ạMN.
Câu 8.b (1,0 đi mể). Trong không gian v i h toa đô ớ ệ Oxyz, cho đ ng th ng ườ ẳ
∆
:
2 1 5
1 3 2
x y z
+ − +
= = −
và hai
đi m ểA (-2; 1; 1); B (-3; -1; 2). Tìm t a đ đi m ọ ộ ể M thu c đ ng th ng ộ ườ ẳ
∆
sao cho tam giác MAB có di n tíchệ
b ng ằ
3 5
.
Câu 9.b (1,0 đi mể). Cho s ph c ố ứ z th a mãn ỏ
11
2
z
z i
−=
−
. Tìm s ph c ố ứ z bi t ế
35
2
z i
+ −
đ t giá tri nh nh t.ạ ỏ ấ
1
Câu N i dungộĐi mể
1.1
1. (1,0 đi m)ể Kh o sát... ả
3 2 3
3 4y x mx m= − +
(1) 1,00
Khi m = 1, ta có
3 2
y x 3x 4= − +
* TXĐ:
D
=
ﾡ
* S bi n thiênự ế :
+) Chi u bi n thiên:ề ế
2
' 3 6
= −
y x x
;
2
0
' 0 3 6 0 2
=
= − =� � =
x
y x x x
Hàm s đ ng bi n trên kho ng ố ồ ế ả
( ) ( )
;0 à 2;v
− +
; ngh ch bi n trên kho ng ị ế ả
( )
0;2
0,25
+ ) Hàm s đ t c c đ i t i x = 0, yố ạ ự ạ ạ CĐ = 4; đ t c c ti u t i x = 2, yạ ự ể ạ CT = 0
+ ) Gi i h n:ớ ạ
3 2
lim ( 3 4)
x
x x
−
− + = −
3 2
lim ( 3 4)
x
x x
+
− + = +
0,25
+) B ng bi n thiên: ả ế
x
−∞
0 2
+∞
y
′
+ 0
−
0 +
y
4
+
−∞
0
0,25
* Đ th : ồ ị
y
4
-1 0 2 3 x
0,25
1.2
Xác đ nh m đ ....ị ể 1,00
Ta có
2
0
3 6 ; 0 2
x
y x mx y x m
=
= − = =
. Đ th hàm s có hai c c tr t i A và B khi và chồ ị ố ự ị ạ ỉ
khi
2 0 0m m
�۹
(
∗
)
0,25
Khi đó: G i A(0; 4mọ3) và B(2m; 0); t gi thi t: ừ ả ế
2 2
20OA OB
+ =
, suy ra:
6 2 6 2
16 4 20 4 5 0m m m m
+ = + − =�
0,25
( ) ( ) ( )
( )
2 4 2 2
0,
1 4 4 5 0 1 0 1( )
m
m m m m m TM
∀�
− + + = − = = ∗� � �
1 4 42 4 43
0,25
2
V y m = ậ
1
. 0,25
2
Gi i ph ng trình: ả ươ
3 sin 2 os2 4 3(cos 3 s inx)x c x x− + = +
(1) 1,00
Đ t t = cosx + ặ
3
sinx
2 2 2
2
1 os2 1 os2
os 3sin 3 sin 2 3 3 sin 2 2 os2 3 sin 2
2 2
3 sin 2 os2 2
c x c x
t c x x x x c x x
x c x t
+ −
= + + = + + = − +�
− = −�
0,25
Khi đó, (1) tr thành: tở2 – 2 + 4 = 3t
2
1
3 2 0 2
t
t t t
=
− + =� � =
0,25
+) t = 1 thì:
22
cos 3 s inx 1 os os 3
3 3 2
x k
x c x c
x k
ππ
π π
π
= +
� �
+ = − =� �
� �
� � =
+) t = 2 thì:
cos 3 s inx=2 cos( ) 1 2
3 3
x x x k
π π π
+ − = = +� �
0,25
V y ph ng trình có 3 h nghi m: ậ ươ ọ ệ
22 ; 2 ; 2
3 3
x k x k x k
π π
π π π
= + = = +
0,25
3
•Gi i h ph ng trìnhả ệ ươ
( )
( ) ( )
2
1 2 17 0
4 32
x xy y
x y xy
+ + + − =
+ + =
1,00
H đã cho t ng đ ng v i: ệ ươ ươ ớ
( ) 2( ) 16
( )( 4) 32
x x y x y
x y xy
+ + + =
+ + =
16 ( )( 2) (1)
( )( 4) 2.16 (2)
x y x
x y xy
= + +
+ + =
0,25
Th (1) vào (2) đ c: ế ượ
( ) ( ) ( ) ( )
x y xy 4 2 x y x 2
+ + = + +
( ) ( )
2 0x x y y
+ − =�
0; 0; 2.x x y y
= + = =�
0,25
+) x = 0 thay vào (1) đ c: y = 8ượ
+) x + y = 0 thay vào (1) đ c: 0x = 16 (VN)ượ
+) y = 2 thay vào (1) đ c: x = 2 ho c x = -6ượ ặ 0,25
V y h đã cho có ba nghi m: ậ ệ ệ (0; 8); (2; 2); (-6; 2) 0,25
4
Tính tích phân
2
2
1
2ln
( 2)
x x
I dx
x
+
=+
1,00
Đ t ặ
( )
2
2
2ln
11
22
x
u x x du dx
x
dv dx v
xx
+
= +
=
� �
� �
=−
� � =
+
+
0,25
22
11
2ln
2
x x dx
Ix x
+
= − +
+
0,25
=
1 1 2
6 2
n
− −
+
2
1
ln x
=
ln 2 1
2 6
−
0,25
V y I = ậ
ln 2 1
2 6
−
. 0,25
5•Tính th tích ...ể1,00
G i I là trung đi m AC, do ọ ể
SAC
∆
cân t i S nên ạ
( )SI ABC
⊥
. G i H là trung đi m AIọ ể 0,25
3
suy ra MH//SI
( )MH ABC
⊥�
, do đó (MN,(ABC)) =
MNH
= 60
0
. Ta có
2
2
ABC
a
S=
.
Xét
HCN
∆
có:
2
2 2 2 0
3 2 5
; ; 2 . . os45
2 4 8
a a a
NC HC NH HC NC HC NC c
= = = + − =
;
10
4
a
NH
=
0 3
.
30 30 1 30
ó tan 60 ; 2 .
4 2 3 12
S ABC ABC
Trong MHNc MH NH a SI MH a V SI S a
∆ = = = = = =�
0,25
Goi J là trung đi m AB, K là hình chi u vuông góc c a H lên MJ t c là ể ế ủ ứ
HK MJ
⊥
(1).
Ta có
( )
( ) ( ) ( ) ( )
( ) ( ) ( )
, à / / 2
/ / , à (3)
2 , 3 4
1 , 4
JN BI m BI HJ JN HJ
SI MH m SI JN JN MH
JN MHJ HK HK JN
HK MNJ
⊥ ⊥�
⊥ ⊥�
⊥ ⊥� � �
⊥�
0,25
( , ) ( , ) ( , ( ))d AC MN d H AC MN d H MJN HK
= = =�
S
=
2 2
.MH HJ
MH HJ
+
=
2 2
30 2
.30
4 4
16
30 2
16 16
a a
a
a a
=
+
M
K
A H I
C
J
N
B
0,25
6Tìm giá tr l n nh t c a bi u th c ..................ị ớ ấ ủ ể ứ 1,00
áp d ng B t đ ng th c: ụ ấ ẳ ứ
2
( ) 3( )x y z xy yz zx+ + + +
,
, ,x y z
∀��
ta có:
2
( ) 3 ( ) 9 0ab bc ca abc a b c abc+ + + + = >
3ab bc ca abc+ +� �
Ta có:
3
3
(1 )(1 )(1 ) (1 ) , , , 0a b c abc a b c
+ + + + ∀ >
. Th t v y:ậ ậ
( ) ( ) ( )
2 3
3 3
3
1 1 1 1 ( ) ( ) 1 3 3 ( ) (1 )a b c a b c ab bc ca abc abc abc abc abc
+ + + = + + + + + + + + + + = +
0,25
Khi đó:
3
3
2
3(1 ) 1
abc
P Q
abc abc
+ =
+ +
(1).
Đ t ặ
6
abc t
=
; vì a, b, c > 0 nên
3
0 1
3
a b c
abc
+ +
� �
< =
� �
� �
0,25
Xét hàm s ố
(
]
2
3 2
2, 0;1
3(1 ) 1
t
Q t
t t
= +
+ +
( )
( )
( ) ( )
(
]
5
2 2
3 2
2 1 1
( ) 0, 0;1
1 1
t t t
Q t t
t t
− −
= ∀� � �
+ +
.
Do đó hàm s đ ng bi n trên ố ồ ế
(
]
0;1
( ) ( )
1
16
Q Q t Q
= =� �
(2). T (1) và (2): ừ
1
6
P
.
0,25
4
V y maxP = ậ
1
6
, đ t đ c khi và và chi khi : ạ ượ
1a b c
= = =
. 0,25
7.a
Tìm t a đ đ nh c a hình ch nh tọ ộ ỉ ủ ữ ậ 1,00
T a đ I là nghi m c a h : ọ ộ ệ ủ ệ
3 0
6 0
x y
x y
− − =
+ − =
9 3
( ; )
2 2
I
. G i M là trung đi m c a AD,ọ ể ủ
T a đ c a M là nghi m c a h ọ ộ ủ ệ ủ ệ
0(3;0)
3 0
yM
x y
=
− − =
0,25
Suy ra AB = 2 IM = 3
2
. M t khác ặ
12
. 2 2
3 2
ABCD
ABCD
S
S AB AD AD AB
= = = =�
. Vì M,
I cùng thu c ộ
1
d
suy ra AD
1
d
⊥
. V y AD đi qua đi m M và nh n ậ ể ậ
(1;1)n
=
r
làm véc tơ
pháp tuy n có ph ng trình:ế ươ
3 0 3 0x y x y
− + = + − =�
.
0,25
L i có MA = MD = ạ
2
2
AD
=
. T a đ đi m A, D là nghi m c a họ ộ ể ệ ủ ệ
( )
22
3 0 2 4
1 1
3 2
x y x x
y y
x y
+ − =
= =
� �
� �
� � �
= = −
− + = � �
. Ch n ọ
(2;1); (4; 1)A D
−
0,25
Các đi m C, B l n l t đ i x ng v i A, B qua I. Suy ra t a đ đi m C(7; 2); B(5;4)ể ầ ượ ố ứ ớ ọ ộ ể 0,25
8.a
•Tìm t a đ đi m Mọ ộ ể 1,00
Vì M
d
nên
( )
1 ; 2 2 ; 2M t t t
+ − + −
. Tr c Oz đi qua đi m O(0; 0; 0) và có vtcpụ ể
( )
0;0;1k=
r
; 0,25
( )
1 ; 2 2 ; 2OM t t t= + − + −
uuuur
. Suy ra:
( )
2
; 2 2 ; 1 ;0 ; 5 6 5OM k t t OM k t t
� � � �
= − + − − = − +�
� � � �
uuuur uuuur
r r
0,25
G i R là bán kính m t c u (S), ta có R = d(M; Oz) = ọ ặ ầ
2
5 6 5t t
− +
0,25
R = 2 suy ra
2
5 6 5t t
− +
= 2
2 2
5 6 5 4 5 6 1 0t t t t
− + = − + =� �
1
1
5
t
t
=
=
( )
2;0; 2
6 8 2
; ;
5 5 5
M
M
−
� �
−
� �
� �
0,25
9.a
Tìm Ph n th c c a wầ ự ủ 1,00
2 (1 2 ) 2 4
1 2
zz z i z i
i
+ = + − = −�
−
(1) . Đ t z = a + bi (ặ
,a b
��
) 0,25
(1) tr thành: a + bi + (1 – 2i)(a - bi) =2 – 4i ở
( )
2 2 2 2 4a b ai i
− − = −�
0,25
2 4 2 2
2 2 2 1
a a z i
a b b
− = − =
� � = +� � �
� �
− = =
� �
0,25
2
w 1 3z z i
= − = +
. V y ph n th c c a w b ng 1.ậ ầ ự ủ ằ 0,25
7.b
Vi t pt đ ng th ng MNế ườ ẳ 1,00
Ta có I(1;-2) suy ra
(0; 2)IA
=
uur
. Tam giác AMN cân khi IA vuông góc MN. G i (d) làọ
đ ng th ng vuông góc v i IA, nên (d) nh n ườ ẳ ớ ậ
làm véc t pháp tuy n, PT (d)ơ ế
0,25
5